中等学校招生初三数学考试

中等学校招生初三数学考试

第Ⅰ卷

一、（3×12＝36）

1.等于（　 ）

（A）2　　 （B）－2　　 （C）2　　 （D）－2

2.下列运算正确是是（　 ）

（A）x·x³＝x³　　　　　　　　　  （B）x²＋x²＝x⁴　

（C）（－4xy²）²＝－8x²y⁴　　　　　 （D）(－2x²）(-4x³)＝8x⁵

3.函数y＝中自变量x的取值范围是（　 ）

（A）x≥2　　 （B）x≤2　　（C）x≤2且x≠0　（D）x＜2

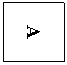
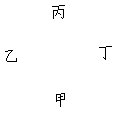4.如图，甲、乙、丙、丁四人分别坐在一方桌的四个不同

方向上，看到桌面上的图案呈“A”种形状的是（　 ）

（A）甲　　 （B）乙　　（C）丙　　 （D）丁

5.在今年的“两会”上，温家宝总理在政府工作报告中

提出，要在五年之内，在全国逐步取消农业税，减轻

农民负担。目前我国农民每年交纳的农业税约为300亿

元，用科学计数法表示为（结果保留三个有效数字）

（A）3.00×10¹⁰元　　　　  （B）3×10¹⁰元　

（C）3×10¹¹元　　　　　  （D）3.00×10¹¹元　

6.用9根同样长的火柴棒在桌面上摆一个三角形（不允许将火柴棒折断，并且全部用完），能摆出不同形状的三角形的个数是（　 ）

（A）1　　 （B）2　　 （C）3　　 （D）4

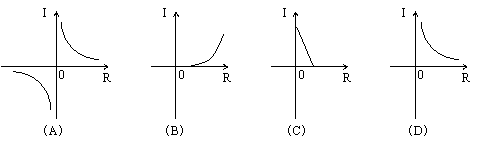
7.在公式I＝中，当电压U一定时，电流I与电阻R之间的函数关系可用图象表示为（　 ）

8.△ABC是直径为10cm的⊙O的内接等腰三角形，如果此等腰三角形的底边BC＝8cm，则该△ABC的面积为（　 ）

（A）8cm²　 （B）12cm²　 （C）12cm²或32cm²　 （D）8cm²或32cm²

9.已知关于x的方程k²x²－（2k－1）x＋1＝0有两个不相等的实数根，那么使该方程的两个实数根互为相反数的k的值是（　 ）

（A）不存在　 （B）1　　（C）－1　　 （D）

10.如图是一块矩形ABCD的场地，长AB＝102m，宽AD＝51m，从A、

B两处入口的小路宽都为1m，两

小路汇合处路宽为2m，其余部分

种植草坪，则草坪面积为（　 ）

（A）5050m²　　（B）4900m²

（C）5000m²　　（D）4998m²

11.某商品降价20％后出售，一段时间后欲恢复原价，则应在售价的基础上提高的百分数是（　 ）

（A）20％　　（B）30％　　（C）35％　　（D）25％

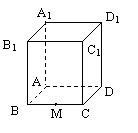
12.如图，正方体盒子的棱长为2，BC的中点为M，

一只蚂蚁从M点沿正方体的表面爬到D₁点，蚂

蚁爬行的最短距离是（ 　）

（A）　 （B）3　　（C）5　 （D）2+

第Ⅱ卷

二、填空题（3×5＝15）

13.若代数式x²＋3x－5的值为2，则代数式2x²+6x－3的值为　　　　。

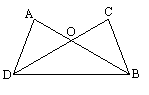14.如图，AB、CD相交于点O，AB＝CD，请你补充一个条件，使得△AOD≌△COB。你补充的条件是　　　　 。

15.若一次函数的图象经过反比例函数y＝－

图象上的两点（1，m）和（n，2），则这个

一次函数的解析式是：　　　　　  。

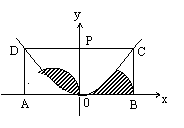
16.如图，矩形ABCD的长AB＝4cm，宽AD＝

2cm，O是AB的中点，OP⊥AB，两半圆的直径

分别为AO与OB。抛物线的顶点是O，关于OP

对称且经过C、D两点，则图阴影部分的面积

是　　　　cm²。

17.科学发现：植物的花瓣、萼片、果实的数目以及其他方面的特征，都非常吻合于一个奇特的数列——著名的斐波那契数列：1,1,2,3,5,8,13,21,34,55，……仔细观察以上数列，则它的第11个数应该是　　  。

三、解答题

18.（8分）

解方程组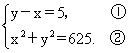

19.（8分）小明去玻璃店买一块长为40cm，宽为30cm的矩形玻璃。店主划好后，小名想利用玻璃店内的现有工具验证店主所划玻璃是否符合要求。请你帮助小明设计一种验证方案（玻璃店内可选用的工具有米尺、曲尺）。

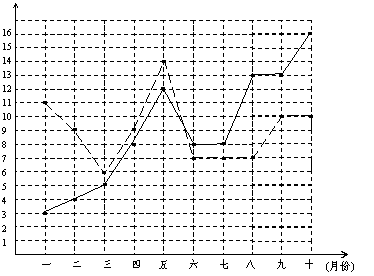20.某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：

（1）请你根据上图填写下表：

销售公司	平均数	方差	中位数	众数
甲			9
乙	9	17.0		8

（2）请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：

①从平均数和方差结合看；

②从折线图上甲、乙两个汽车销售公司销售数量的趋势看（分析哪个汽车销售公司较有潜力）。

21.（8分）

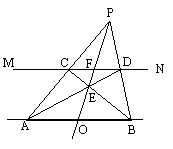在一次数学活动课上，一位同学提出：“谁能帮我用没有刻度的三角板找出线段AB的中点？”小华说：“我能做到。我的做法是，用这副三角板任作一条直线MN∥AB；在直线AB、MN的同一侧任取一点P，连结PA、PB，分别交直线MN于C、D；再连结AD、BC，相交于点E；画射线PE交线段AB于点O，点O就是线段AB的中点。”你认为点O是线段AB的中点吗？并说明理由。

22.（8分）

我市某县素以“中国蒜都”著称。某运输公司计划用10辆汽车将甲、乙、丙三种大蒜共100吨运输到外地，按规定每辆车只能装同一种大蒜，且必须满栽，每种大蒜不少于一车。

（1）设用x辆车装运甲种大蒜，用y辆车装运乙种大蒜。根据下表提供的信息，求y与x之间的函数关系式，并求自变量x的取值范围；

（2）设此次运输的利润为M（百元），求M与x的函数关系式及最大运输利润，并安排此时相应的车辆分配方案。

大蒜品种	甲	乙	丙
每辆汽车的满载量（吨）	8	10	11
运输每吨大蒜获利（百元）	2.2	2.1	2

21.（9分）

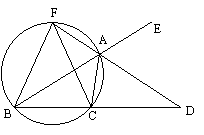
如图，AD是△ABC外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F。

（1）求证：FB＝FC；

（2）若FA＝2，AD＝4，求FB的长。

24.（10分）阅读下列材料：

在计算1+4+7+10+13+16+19+22+25+28时，我们发现，从第一个数开始，以后的每个数与它的前一个数的差都是一个相同的定值。具有这种规律的一列数，求和时，除了直接相加外，我们还可以用公式S＝na＋×d来计算（公式中的S表示它们的和，n表示数的个数，a表示第一个数的值，d表示这个相差的定值）。

那么S＝1+4+7+10+13+16+19+22+25+28

＝10×1＋×3＝145.

用上面的知识解决下列问题：

我市某乡镇具有“中国北方乔木之乡”的美称，到2000年底这个镇已有苗木2万亩，为增加农民收入，这个镇实施“苗木兴镇”战略，逐年计划扩种苗木。从2001年起，以后每年又比上一年多种植相同面积的苗木；从2001年起每年卖出成苗木，以后每年又比上一年多卖出相同面积的成苗木。下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据。

年份	2001年	2002年	2003年
每年种植苗木的面积（亩）	4000	5000	6000
每年卖出成苗木的面积（亩）	2000	2500	3000

假设所有苗木的成活率都是100%，问到哪一年年底，这个镇的苗木面积达到5万亩。

25.（10分）

已知抛物线y＝x²－（2m-1）x＋4m－6。

（1）试说明对于每一个实数m，抛物线都经过x轴上的一个定点；

（2）设抛物线与x轴的两个交点A（x₁，0）和B（x₂，0）（x₁＜x₂）分别在原点的两侧，且A、B两点间的距离小于6，求m的取值范围；

（3）抛物线的对称轴与x轴的交于点C（，0），在（2）的条件下，试判断是否存在m的值，使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D，且被x轴截得的劣弧CD是等弧。若存在，求出所有满载条件的m的值，若不存在，说明理由。