中考模拟试卷
一.选择题
1. 下列各数:![]() 、0.32、
、0.32、![]() 、
、![]() 、0.…中是无理数的有(
)
、0.…中是无理数的有(
)
A. 1个 B. 2个 C. 3个 D. 4个
2. 过点![]() 的正比例函数解析式是( )
的正比例函数解析式是( )
A、![]() ; B、
; B、![]() ; C、
; C、![]() ; D、
; D、![]()
3. 某物体的三视图是如图1所示的三个图形,那么该物体形状是( )
A. 长方体
长方体
B. 圆锥体
C.立方体
D.圆柱体
4. 某种品牌的产品共100件,其中有5件次品,小王从中任取一件,则小王取到次品的概率是( )
A、0.5 B、0.05 C、0.95 D、0.095
5.下列运算中
(1) ![]() (2)
(2)
![]() (3)
(3)
![]()
(4) ![]() (5)
(5) ![]()
其中正确的运算有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
6.在一个四边形ABCD中,依次连结各边中点的四边形是菱形,则对角线AC与BD需要满足条件 ( )
A. 垂直 B. 相等 C.垂直且相等 D. 不再需要条件
7.样本甲的方差是![]() ,样本乙的数据为2.20,2.30,2.20,2.10,2.20,则样本甲和样本乙波动大小为 ( )
,样本乙的数据为2.20,2.30,2.20,2.10,2.20,则样本甲和样本乙波动大小为 ( )
A.甲、乙波动大小一样 B.乙的波动比甲的波动大
C.甲的波动比乙的波动大 D.甲、乙的波动大小无法比较
8. 宾馆客房的标价影响住宿百分率,下表是某一宾馆在近几年旅游周统计的平均数据:
| 客房价(元) | 160 | 140 | 120 | 100 |
| 住宿百分率 | 63.8% | 74.3% | 84.1% | 95% |
在旅游周,要使宾馆客房收入最大,客房标价应选:
(A)160元 (B)140元 (C)120元 (D)100元
9. 边长相等的下列两种正多边形的组合,不能作平面镶嵌的是( )
A.正方形与正三角形 B.正五边形与正三角形
C.正六边形与正三角形 D.正八边形与正方形
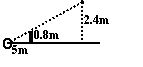 10. 小芳在打网球时,为使球恰好能过网(网高为0.8m),且落在对方区域离网5m的位置上,已知她击球的高度是2.4m,则她应站在离网的
10. 小芳在打网球时,为使球恰好能过网(网高为0.8m),且落在对方区域离网5m的位置上,已知她击球的高度是2.4m,则她应站在离网的
(A)15m处 (B)10m处 (C)8m处 (D)7.5m处
11. 如图,一束光线从y轴点A(0,2)出发,经过x轴
|
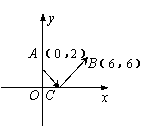 上点C反射后经过点B(6,6),则光线从点A到点
上点C反射后经过点B(6,6),则光线从点A到点
B所经过的路程是 ( )
A.10 B.8
C.6 D.4
![]()
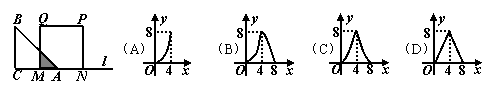 12.如图,等腰直角三角形ABC(∠C=Rt∠)的直角边长与正方形MNPQ的边长均为4cm,CA与MN在直线l上。开始时A点与M点重合,让△ABC向右平移,直到C点与N点重合时为止。设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm,则y与x之间的函数关系大致是
12.如图,等腰直角三角形ABC(∠C=Rt∠)的直角边长与正方形MNPQ的边长均为4cm,CA与MN在直线l上。开始时A点与M点重合,让△ABC向右平移,直到C点与N点重合时为止。设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm,则y与x之间的函数关系大致是
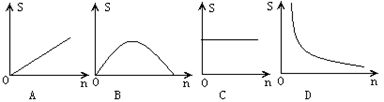
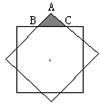
12. 如图,两块完全重合的正方形纸片,如果上面的一块绕正方形的中心O左0°~90°的旋转,那么旋转时露出的△ABC的面积(S)随着旋转角度(n)的变化而变化,下面表示S与n关系的图象大致是( )
![]() 二、填空题(每题3分,共24分)
二、填空题(每题3分,共24分)
13. 圆和圆有不同的位置关系.与下图不同的圆和圆的位置关系是_____.(只填一种)

14. 已知![]() 是方程
是方程![]() 的一个根,那么代数式
的一个根,那么代数式![]() ;
;
15.一个圆锥形的蛋筒,底面圆直径为7cm,母线长为14cm,把它的包装纸展开,侧面展开图的面积为__________________cm2(不计折叠部分).
16. 一杯可乐售价1.8元,商家为了促销,顾客每买一杯可乐获一张奖券,每三张奖券可兑换一杯可乐,则每张奖券相当于
(A)0.6元 (B)0.5元 (C)0.45元 (D)0.3元
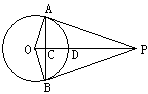 17. 如图,P是⊙O外一点,OP垂直于弦AB于点C,交
17. 如图,P是⊙O外一点,OP垂直于弦AB于点C,交![]() 于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):
于点D,连结OA、OB、AP、BP。根据以上条件,写出三个正确结论(OA=OB除外):
①
;②
;③
。
18.有一根70㎝的木棒放在长、宽、高分别为30㎝、40㎝、50㎝的长方形木箱中,能放进去吗?答____________.
 19. 如图,在△ABC中,AB=BC=AC=3,O是它的内心,以O
19. 如图,在△ABC中,AB=BC=AC=3,O是它的内心,以O
为中心,将△ABC旋转180°得到△![]() ,则△ABC与△
,则△ABC与△
![]() 的重叠部分的面积为
.
的重叠部分的面积为
.
20. 学生李军在一次数学活动课中,将一圆形纸板,经过多次剪裁,把它剪裁成若干个扇形.操作要求:第1次剪裁,将圆形纸板等分成4个扇形;第2次剪裁,将上次得到的扇形中的一个再等分成4个扇形;以后按第2次剪裁的做法进行下去.请你结合他的剪裁过程填表:
| 剪裁次序 | 1 | 2 | 3 | … | 10 |
| 所得扇形总个数 | 4 | 7 | … |
三、计算题
21. 计算![]()
22. 先化简,再求值.![]() 其中
其中![]()
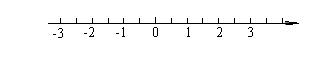 23. 解不等式组 并把解集在数轴上表示出来.
23. 解不等式组 并把解集在数轴上表示出来.
24. 如图,在△AFD和△BEC中,点A、E、F、C在同一条直线上,有下面四个论断:
 ①AD=CB,②AE=CF,③∠B=∠D,④AD∥BC。请你用其中三个作为条件,余下一个作为结论,编一道数学题,并写出解答过程
①AD=CB,②AE=CF,③∠B=∠D,④AD∥BC。请你用其中三个作为条件,余下一个作为结论,编一道数学题,并写出解答过程
已知:
求证:
证明:
25. 某商场设立了一个可以自由转动的转盘(如图),并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品。下表是活动进行中的一组统计数据:
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在铅笔的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在铅笔的频率 |
(1)计算并完成表格
(2)请估计,当很大时,频率将会接近多少?
(3)假如你去转动转盘一次,你获得铅笔的概率约时多少?
(4)在该转盘中,标有“铅笔”区域的扇形的圆心角大约是多少?(精确到1°)

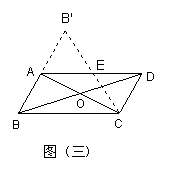
26.如图,在![]() 的纸片中,AC⊥AB,AC与BD相交于O,将△ABC沿对角线AC翻转180°,得到
的纸片中,AC⊥AB,AC与BD相交于O,将△ABC沿对角线AC翻转180°,得到![]() .
.
(1)求证:以A、C、D、![]() 为顶点的四边形是矩形;
为顶点的四边形是矩形;
 (2)若四边形ABCD的面积S=12cm2.
求翻转后纸片重叠部分的面积,即
(2)若四边形ABCD的面积S=12cm2.
求翻转后纸片重叠部分的面积,即![]() .
.
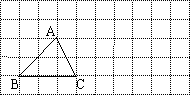
26. 如图,在10×5的正方形网格中,每个小正方形的边长均为单位1,将△ABC向右平移4个单位,得到△A′B′C′,再把△A′B′C′绕点A′逆时针旋转90°,得到△A″B″C″.请你画出△A′B′C′和△A″B″C″(不要求写画法)

27. 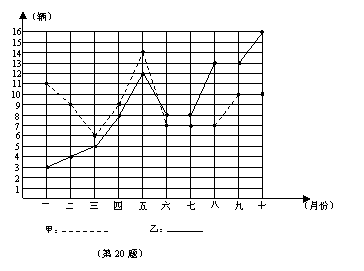 某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据上图填写下表:
| 销售公司 | 平均数 | 方差 | 中位数 | 众数 |
| 甲 | 9 | |||
| 乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).
28. 某市认真落实国家关于减轻农民负担,增加农民收入的政策,从2004年开始减征农业税,2003年至2005年征收农业税变化情况见表(1),2005年市政府为了鼓励农民多种粮食,实行保护价收购,并对种植优质水稻(如中籼稻)另给予每亩15元的补贴.该市农民李江家有4个劳动力,承包20亩土地,今年春季全部种植中籼稻和棉花,种植中籼稻和棉花每亩所需劳力和预计每亩平均产值见表(2).设2005年李江家种植中籼稻和棉花的预计总收入为P元,种植中籼稻的土地为![]() 亩.
亩.
|
| 年份 | 2003 | 2004 | 2005 |
| 农业税(元/亩) | 117.24 | 70.44 | 38.26 |
|
| 农作物 | 产值(元/亩) | 劳力(人/亩) |
| 中籼稻 | 785 | 0.15 |
| 棉花 | 1200 | 0.35 |
(1) 李江家从国家开始减征农业税后两年可少交农业税多少元?
(2)
若不考虑上缴农业税,请写出P(元)与![]() (亩)的函数关系式.
(亩)的函数关系式.
(3) 李江家在不考虑他人帮工等其它因素的前提下,怎样安排中籼稻和棉花的种植面积才能保证P最大?最大值是多少?
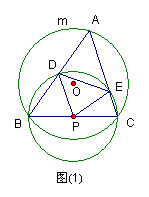
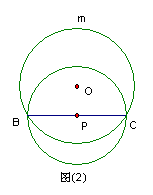
29.如图,⊙O与⊙P相交于B、C两点,BC是⊙P的直径,且把⊙O分成度数的比为1:2的两条弧,A是![]() 上的动点(不与B、C重合),连结AB、AC分别交⊙P于D、E两点.
上的动点(不与B、C重合),连结AB、AC分别交⊙P于D、E两点.
(1)当△ABC是锐角三角形(图①)时,判断△PDE的形状,并证明你的结论;
(2)当△ABC是直角三角形、钝角三角形时,请你分别在图②、图③中画出相应的图形(不要求尺规作图),并按图①标记字母;
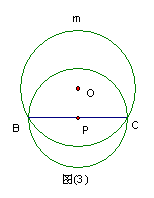
 (3)在你所画的图形中,(1)的结论是否成立?请就钝角的情况加以证明.
(3)在你所画的图形中,(1)的结论是否成立?请就钝角的情况加以证明.
![]()
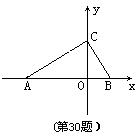
30.如图12,A、B两点的坐标分别是(![]() )、(
)、(![]() ),其中
),其中![]() 、
、![]() 是关于x的方程
是关于x的方程![]() 的两根,且x
的两根,且x![]() <0<x
<0<x![]() .
.
(1)求m的取值范围;
(2)设点C在y轴的正半轴上,∠ACB=![]() ,∠CAB=
,∠CAB=![]() ,求经过A、B、C三点的抛物线解析式;
,求经过A、B、C三点的抛物线解析式;
 (3)在求得的抛物线上,是否存在点D,使△DAB≌△CBA,若存在,求出直线AD的函数解析式,若不存在,说明理由.
(3)在求得的抛物线上,是否存在点D,使△DAB≌△CBA,若存在,求出直线AD的函数解析式,若不存在,说明理由.