中考模拟试题
填空题：
1、纳米是一种长度单位，1纳米＝10－9米，已知某种植物花粉的直径为35000纳米，那么用科学记数法表示该花粉的直径为 米；
2、分解因式:
=_____________________；
3、 如图，
是△
的中位线，则△
与△的周长之比为
；
4、某商品的进价是500元，标价为750元，商店要求以不低于5%的利润打折出售，售货员最低可以打__________折；
5、已知a是整数，点A(2a+1，2+a)在第二象限，则a= ；
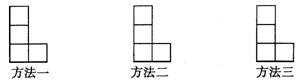6、如图，由小正方形组成的L形图中，请你用三种方法分别在下图中添画一个小正方形使它成为轴对称图形：
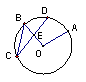
7、如图，点A、B、C、D是圆O上四点，且点D是弧AB 的中点，CD交OB于E，∠AOB=100°，∠OBC=55°，则∠OEC=__________度；
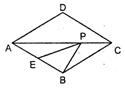8、如图，菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是 ；
9、已知一个二次函数的顶点坐标为（1，2），请你写一个符合条件的二次函数的表达式： ；
10、有一大捆粗细均匀的电线，现要确定其长度的值。从中先取出1米长的电线，称出它的质量为a，再称其余电线的总质量为b，则这捆电线的总长度是 米。
二、选择题：
1、下列用英文字母设计的五个图案中既是轴对称图形，又是中心对称图形的有( )
(A) 0个 (B) 1个 (C) 2个 (D)3个
2、下列长度的三根木棒首尾相接，不能做成三角形框架的是（ ）
（A）5、7、10（B）7、10、13（C）5、7、13（D）5、10、13
3、在
中，
，如果
，那么
的值等（ ）
A. 
B.
C.
D.
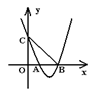
4、如图，抛物线
与
轴交于
、
两点，与
轴交于点
，
，则下列各式成立的是（ ） A．
B．
C．
D．
5、某药店经营的抗病毒药品，在市场紧缺的情况下提价100%，物价部门查处后，限定其提价的幅度只能是原价的10%，则该药品现在降价的幅度是（ ）
A．45% B．50% C．90% D．95%．
6、一种花边是由如图的弓形组成的， 弧ACB的半径为5，弦AB=8，则弓形的高CD为（ ）
A：2 B：
C：3 D：
三、解答题：
1、已知：
求
的值。
2、某机械化养鸡场有一批同时开始饲养的良种鸡1000只，任取10只，称得其质量情况表如下：
| 鸡的质量(单位：kg) | 2．0 | 2．2 | 2．4 | 2.9 | 2．6 | 3．0 |
| 鸡的数量(单位：只) | 1 | 2 | 3 | 2 | 1 | 1 |
求：(1)这10只鸡的平均质量为多少kg?
(2)考虑到经济效益，该养鸡场规定质量在2．2kg以上(包括2．2kg)的鸡才可以出售，请估计这批鸡中有多少只可以出售?
3、杨嫂在再就业中心的扶持下，创办了“润扬”报刊零售点.对经营的某种晚报，杨嫂提供了如下信息：
①买进每份
元，卖出每份
元；
②一个月内（以
天计），有
天每天可以卖出
份，其余
天每天只能卖出
份；
③一个月内，每天从报社买进的报纸份数必须相同.当天卖不掉的报纸，以每份
元退回给报社；
⑴填表：
| 一个月内每天买进 该种晚报的份数 |
|
|
| 当月利润（单位：元） |
|
|
⑵设每天从报社买进该种晚报份
时，月利润为元，试求出与的函数关系式，并求月利润的最大值.
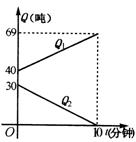4、某空军加油飞机接到命令，立即给另一架正在飞行的运输飞机进行空中加油．在加油过程中，设运输飞机的油箱余油量为
吨，加油飞机的加油油箱余油量为
吨，加油时间为t分钟，、与t之间的函数图象如图所示，结合图象回答下列问题：
（1）加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?（2）求加油过程中，运输飞机的余油量（吨）与时间t（分钟）的函数关系式；（3）运输飞机加完油后，以原速继续飞行，需10小时到达目的地，油料是否够用?说明理由．
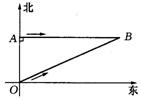5、人民海关缉私巡逻艇在东海海域执行巡逻任务时，发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只，正以24海里／小时的速度向正东方向航行．为迅速实施检查，巡逻艇调整好航向，以26海里／小时的速度追赶，在涉嫌船只不改变航向和航速的前提下，问⑴需要几小时才能追上？（点B为追上时的位置）⑵确定巡逻艇的追赶方向（精确到0．1°）．
参考数据：
sin66．8°≈ 0．9191
cos 66．8°≈ 0．393
sin67．4°≈ 0．9231
cos 67．4°≈ 0．3846
sin68．4°≈ 0．9298
cos 68．4°≈ 0．368l
sin70．6°≈ 0．9432
cos70．6°≈ 0．3322
6、汽车行驶中，司机从判断出现了紧急情况到进行刹车时，这一段汽车走过的路程称为刹车反应距离。某研究机构收集了有关刹车反应距离的数据如下表：
| x | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
| y | 22 | m | 33 | 38.5 | 44 | 50 | 55 | n | 66 | 71 | 77 | 82.5 | 88 |
表中x为汽车行驶速度（英里/小时），y为刹车反应距离（英尺）；m、n为丢失的数据。由表中给出的有序实数对，在直角坐标系中对应的点如图所示。
⑴请用平滑曲线顺次连结图中各点后，估计y与x的关系最近似于哪一种函数关系，并说明估计的理由；
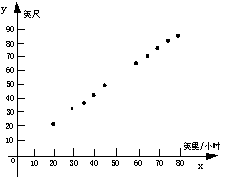⑵请利用估计得到的函数关系中，求出表中m、n 的值。
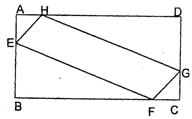
7、为了美化校园环境，某中学准备在一块空地(如图，矩形ABCD，AB=10m，BC=20m)上进行绿化．中间的一块(图中四边形EFGH)上种花，其他的四块(图中的四个Rt△)上铺设草坪，并要求AE=AH=CF=CG．那么在满足上述条件的所有设计中，是否存在一种设计，使得四边形EFGH(中间种花的一块)面积最大?若存在，请求出该设计中AE的长和四边形EFGH的面积；若不存在，请说明理由．
8、探究规律：如图1，已知直线
∥
，A、B为直线上的两点，C、P为直线上的两点。
（1）请写出图中面积相等的各对三角形： 。
（2）如果A、B、C为三个定点，点P在上移动，那么无论P点移动到任何位置总有：
与△ABC的面积相等；理由是：
。
解决问题：
如图2，五边形ABCDE是张大爷十年前承包的一块土地的示意图，经过多年开垦荒地，现已变成如图3所示的形状，但承包土地与开垦荒地的分界小路（图3中折线CDE）还保留着，张大爷想过E点修一条直路，直路修好后，要保持直路左边的土地面积与承包时的一样多。请你用有关的几何知识，按张大爷的要求设计出修路方案。（不计分界小路与直路的占地面积）
（1）写出设计方案，并在图3中画出相应的图形；
（2）说明方案设计理由。
9、已知：如图，BC为半圆的直径，O为圆心，D是弧AC的中点，四边形ABCD的对角线AC、BD交于点E。
（1）求证：△ABE∽ΔDBC；
（2）已知BC＝，CD＝
，求sin∠AEB的值；
（3）在（2）的条件下，求弦AB的长。
10、卢浦大桥拱形可以近似看作抛物线的一部分，在大桥截面1∶11000的比例图上，跨度AB＝5cm，拱高OC＝0.9cm，线段DE表示大桥拱内桥长，DE∥AB。如图，在比例图上，以直线AB为x轴，抛物线的对称轴为y轴，以1cm作为数轴的单位长度，建立平面直角坐标系，如图8：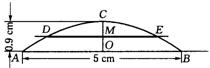
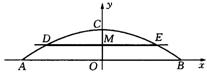
（1）求出图8上以这一部分抛物线为图像的函数解析式，写出函数自变量的取值；
（2）如果DE与AB的距离OM＝0.45cm，求卢浦大桥拱内实际桥长（备用数据：
≈1.4，计算结果精确到1米）