初中数学学科升学模拟练习卷
（考试时间120分钟，满分120分）
（2004/4/25编制 2004/5/11考试）
学校 班级 学号 姓名
考生注意：除第一、二大题以外，其余各题如无特别说明，都必须写出证明或计算的主要步骤．
一、填空题（本大题共14小题、每小题2分，满分28分）：
1、计算：2xy·（－2xy2）3＝ ．
2、因式分解：2a2－ab－2b2＝ ．
|
解是
．
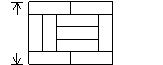4、如图一，由10块相同的长方形地砖拼成的一块
长方形地面图案（地砖间隙不计），如果图案的宽为75
cm，那么图案的的长为 cm．
5、如果
－1是关于x的方程x2＋mx－1＝0的一个解，那么m＝
．．
6、方程x－
＝1的解为
．
7、已知一次函数y＝5x＋b的图象不经过第二象限，那么b的取值范围是 ．
8、顶点是（－1，15），且经过点（2，－3）的二次函数解析式是 ．
9、将一批数据分成5组，列出频率分布表，如果前4组的频率之和为0.85，那么第5组的频率为
．
10、如图二，在△ABC中，CD⊥AB，如果CB
＝20厘米，CD＝12厘米，CA＝15厘米，那么AB
＝
厘米．
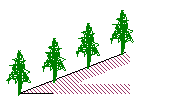
11、如图三，在一段坡度为1︰2的山坡上种树，要
求株距（即相邻两株树之间的水平距离）为6米，那么斜
坡上相邻两株树之间的坡面距离为 米．
  |
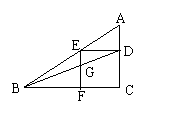12、如图四，在Rt△ABC中，点D、E、F分别在
AC、AB、BC边上，四边形CDEF是正方形，BD与EF
交于点G，如果AC＝9cm，BC＝18cm，那么EG的长
等于 cm．
13、两圆的圆心距为10厘米，一个圆的半径为15厘米．当两圆内切时，另一个圆的半径为 厘米．
14、先作半径为
的圆的内接正三角形，接着作这内接正三角形的内切圆，再作上述的内切圆的内接正三角形……则按以上规律作出的第七个圆的内接正三角形边长为
．
二、多项选择题（本大题共4小题，每小题3分，满分12分）：
[每题列出的四个答案中，至少有一个是正确的，把所有正确答案的代号填入括号内．错选或不选，得0分，否则每漏选一个扣1分，直至扣完为止．]
15、下列因式分解中，错误的是…………………………………………………（ ）
（A）2 x2－2xy－y2＝2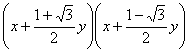
；
（B）4x2－4xy－y2＝（2x－y）2；
（C）m2－5m－6＝（m－2）（m－3）；
（D）4a2－4ab－2b2＝（2a－b＋
b）（2a－b－b）．
16、下列说法中，正确的是………………………………………………………（ ）
（A）函数y＝2x－5的图象不经过第二象限；
（B）函数y＝－5x－1的图象在第二、四象限内；
（C）函数y＝－x＋2的函数值随着x的减小而增大；
（D）函数y＝－8x－1的函数值随着x的增大而增大．
17、如图五，各“风车”型的平面图案中，是中心对称的有…………………（ ）
  |
18、下列说法中，正确的是………………………………………………………（ ）
（A）一组对边平行且一组对角相等的四边形是平行四边形；
（B）每组邻边都相等的四边形是菱形；
（C）三个角相等的四边形是矩形；
（D）对角线互相垂直的平行四边形是正方形．
三、（本大题共4小题，每小题7分，满分28分）：
19、计算：
＋（1＋）2－
＋
．
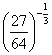20、解方程：
＋
＝14 ．
21、最近，金苹果中学九年级三个班级进行了一次统一测验，图六是各班的语文和数学考试平均分情况表，图七是三个班级学生人数统计表．
 |
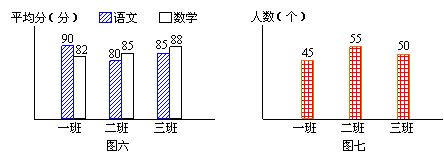（1）求语文考试班级平均分的中位数和数学考试班级平均分的中位数；
（2）求语文考试年级平均分和数学考试年级平均分；
（3）求语文考试班级平均分的方差和数学考试班级平均分的方差；
（4）用一、二句简单的话评论一下金苹果中学九年级三个班级所进行的这次统一测验的结果．
  |
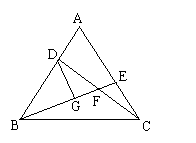22、已知：如图八，在等边△ABC中，点D、E
分别在AB、AC边上，AD＝CE，CD与BE交于点F，
DG⊥BE于点G．
求证：（1）BE＝CD；（2）DF＝2GF．
四、解答题（本大题共4小题，每小题10分，满分40分）：
23、昌盛商店了解到：有一种书包的批发价格是每个40元．当每个标价50元进行销售时，估计能卖出500个．但是售价每提高1元，销售量就会减少10个．另外，商店经营应按销售利润的10%交纳销售税．商店希望通过销售这种书包能净赚纳税后利润7200元．
（1）求每个书包的售价可以定价为多少元？
（2）因为同一个商店在同时同地销售同一件物品时，是不可能有两个定价的，所以如果你是昌盛商店的经理，这时，你会给每个书包定价为多少元（请用一句话说明理由）？并且商店应该批发购进多少个书包？
  |
24、已知：将两块三角板如图九放置，其中∠A＝
∠BCD＝90°，∠ABC＝45°，∠DBC＝30°，BC＝10，
求重叠部分△BCE的面积．
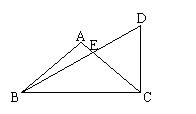
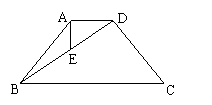25、已知：如图十，在梯形ABCD中，AD∥BC，
AB＝DC，AE⊥AD交BD于点E，∠BAE＝∠BDA，
（1）求证：△ADE∽△DBC；
（2）如果AE＝3，AD＝4，求：梯形ABCD的
周长．
26、抛物线y＝－x2＋（2m＋6）x－（2m2＋7m＋6）与x轴有两个交点A、B（点A在点B的左边），AB＝2，抛物线的顶点是点C，直线y＝kx＋b经过点B、C，与y轴交于点D．
求：（1）抛物线的解析式；（2）△ACD的面积．
五、（本大题满分12分）：
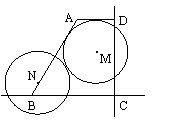27、已知：如图十一，在直角梯形ABCD中，
AD∥BC，∠D＝90°，∠B＝60°，AB＝10cm，
AD＝4cm，⊙M与∠BAD的两边相切，点N在射
线AB上，⊙N与⊙M是等圆，且两圆外切．
（1）如果AN＝xcm，⊙M的半径为ycm，，
求y关于x的函数关系式；
（2）当x为何值时，⊙M与CD相切？
（3）直线CD被⊙M所截得的弦与直线BC被⊙N所截得的弦的长是否可能相等？如果认为可以相等，请求出符合要求的x的值；如果认为不可能相等，请说明理由．
初中数学学科升学模拟练习卷
参考答案与评分标准
一、填空题（本题共14小题、每小题2分，满分28分）：
1、－16 x4y7 ． 2、2（a－
b）（a－
b）． 3、－3＜x≤5 ．
4、90 ． 5、2 ． 6、x＝4 ． 7、b≤0 ．
8、y＝－2（x＋1）2＋15 ． 9、0.15 ． 10、25 ．
11、3
． 12、2 ．
13、5或25 ．
14、
．
二、多项选择题（本大题共4小题，每小题3分，满分12分）：
[每题列出的四个答案中，至少有一个是正确的，把所有正确答案的代号填入括号内．错选或不选，得0分，否则每漏选一个扣1分，直至扣完为止．]
15、ABC． 16、ABC． 17、BD． 18、AB．
三、（本大题共4小题，每小题7分，满分28分）：
19、解：原式＝
＋（3＋2）－2（＋1）＋
…………………2＋1＋1＋2分
＝＋3＋2－2－2＋
＝4 ．……………………………………………………………………………1分
20、解：设y＝
，则原方程可以化为整式方程y2＋5y－14＝0，………………1分
可以解得y1＝2，y2＝－7 ………………………………………………………………2分
当y1＝2时，＝2，∴x1＝6；当y2＝－7时，＝－7，∴x2＝
．……3分
经检验知：x1＝6和x2＝都不是增根，∴原方程的解为x1＝6， x2＝．……1分
21、解：（1）各班的语文考试平均分的中位数是85分，各班的数学考试平均分的中位数是85分．…………………………………………………………………………………………2分
（2）
年级语文＝
＝
≈84.67；…………………………1分
年级数学＝
＝
＝85.1 ．…………………………………1分
（3）∵班级语文＝
＝85，
∴s2语文＝
[（90－85）2＋（80－85）2＋（85－85）2]＝
＝16.67，………………1分
∵班级数学＝
＝85，
∴s2数学＝[（82－85）2＋（85－85）2＋（88－85）2]＝6 ．…………………………1分
（4）这次统一测验的结果表明：数学的年级平均分较高，并且各班的数学学习情况较为稳定． ……………………………………………………………………………………………1分
22、证明：（1）∵△ABC是等边三角形，∴BC＝CA，∠BCE＝∠A＝60°，………1分
∵AD＝CE， ∴△BCE≌△CAD（SAS），……………………1分
∴BE＝CD．…………………………………………………………………………………1分
（2）∵△BCE≌△CAD， ∴∠BEC＝∠CDA， ……………………………1分
∵∠A＝60°， ∴∠ACD＋∠CDA＝120°，
∴∠ACD＋∠BEC＝120°，
∴∠DFG＝∠CFE＝60°，…………………………………………………………………2分
在△DFG中，∵DG⊥BE，∠FDG＝30°，∴DF＝2GF． ……………………………1分
四、解答题（本大题共4小题，每小题10分，满分40分）：
23、解：（1）设每个书包的售价应该定为x元，依题意得 ……………………………1分
（1－10%）（x－40）〔500－10（x－50）〕＝7200 ．………………………2分
整理，得 x2－140 x＋4800＝0 ．…………………………………1分
解得 x1＝60 ， x2＝80 ． …………………………………2分
答：每个书包的售价可以定价60元或80元． …………………………………………1分
（2）如果我是商店的经理，这时考虑到顾客希望便宜的心理，会给每个书包定价为60元． ………………………………………………………………………………………………1分
8000÷（60－40）＝400 ．…………………………………………1分
答：每个书包的定价为60元，商店应该批发购进400个书包．………………………1分
说明：本题答题开放．商品定价是由多种因素决定的，譬如季节、周围商店里的同种商品价格、顾客的从众心理等等．如果考虑到顾客的便宜无好货的心理而选取定价为60元，也是合理的，同样可以得分．这时
8000÷（80－40）＝200 ．
24、解：作EF⊥BC于点F（如图十二），………………………………………………1分
设EF＝x，则
∵∠A＝90°，∠ABC＝45°，∴∠BCA＝45°，
∴FC＝EF＝x，……………………………………2分
∵∠DBC＝30°，∴ctg∠DBC＝ctg30°＝
，
∴BF＝EF·ctg30°＝x………………………2分
即 ∵BC＝BF＋FC＝10，∴x＋x＝10，…………………………………………………1分
∴x＝5－5，即EF＝5－5…………………………………………………………2分
∴S△BCE＝
BC·EF＝×10（5－5）＝25－25 ．……………………………2分
25、解：（1）∵在梯形ABCD中，AD∥BC，AB＝DC，
∴∠BAD＝∠CDA，∠ADE＝∠DBC． …………………………………………………1分
∵∠BAE＝∠BDA，∴∠DAE＝∠BDC． ………………………………………………1分
∴△ADE∽△DBC． ………………………………………………………………………1分
（2）在△ABE和△DBA中，∵∠BAE＝∠BDA，∠ABE＝∠DBA，
∴△ABE∽△DBA， ………………………………………………………………………2分
∴
＝
＝
， ……………………………………………………………………1分
设AB＝x，BE＝y，在Rt△AED中，∵AE＝3，AD＝4，∴ED＝5，
∴
＝
＝
，可以解得：x＝
，y＝
，即AB＝，BE＝． ……2分
∴DC＝，BD＝BE＋ED＝
，
∵△ADE∽△DBC，∴AD︰BD＝DE︰BC，∴4︰＝5︰BC，∴BC＝
． …1分
∴梯形ABCD的周长为AB＋BC＋CD＋DA＝＋＋＋4＝
．………1分
26、解：（1）∵抛物线与x轴有两个交点A、B，若设A（x1，0）、B（x2，0），
∴x1＋x2＝2m＋6，x1x2＝2m2＋7m＋6，…………………………………………………1分
∵AB＝2，且（x1－x2）2＝（x1＋x2）2－4x1x2，
∴22＝（2m＋6）2－4（2m2＋7m＋6），即m2＋m－2＝0，……………………………1分
∴m 1＝1，m 2＝－2．………………………………………………………………………1分
∴当m 1＝1时，所求的抛物线是y＝－x2＋8x－15；……………………………………1分
当m 2＝－2时，所求的抛物线是y＝－x2＋2x．…………………………………………1分
（2）对于抛物线y＝－x2＋8x－15，可以求得：A（3，0）、B（5，0）、C（4，1），
∴经过点B、C的直线的解析式为y＝－x＋5，∴D（0，5），…………………………2分
∴S△ACD＝S△ABD－S△ABC＝×2×5－×2×1＝4；
…………………………………1分
对于抛物线y＝－x2＋2x，可以求得：A（0，0）、B（2，0）、C（1，1）．
则经过点B、C的直线的解析式为y＝－x＋2，∴D（0，2）．…………………………1分
∴S△ACD＝×2×1＝1 ．…………………………………………………………………1分
五、（本大题满分12分）：
27、解：（1）如图十三，连结AM、MN，作ME⊥AB于点E，
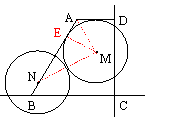∵⊙N与⊙M是等圆，且两圆外切，
∴在Rt△MNE中，MN＝2ME，∠ANM＝30°．…1分
∵⊙M与∠BAD的两边相切，
∴∠NAM＝60°， ∴∠AMN＝90°， …………1分
∴在Rt△AMN中AM＝AN，
当AN＝xcm时，∴AM＝AN＝xcm，
∵ME＝AMcos30°＝
xcm， 即 y＝x（x＞0）．……………………2分
（2）如图十四，当⊙M与CD相切时，作MF⊥AD于点F，MG⊥CD于点G，则
MF＝FD＝MG＝y，且
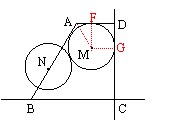AF＝MFtg30°＝
y＝·x＝
x，…1分
∵AD＝4cm，且AF ＋FD＝AD，
∴y＋y＝4，
即 x＋·x＝4， ………………………1分
∴x＝8（－1）．…………………………………………………………………………1分
（3）作NH⊥BC于点H，如果直线CD被⊙M所截得的弦与直线BC被⊙N所截得的弦的长相等，那么弦心距MG＝NH．
可能如图十五，∵AB＝10cm，∴BN＝（10－x）cm，
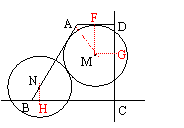∴NH＝BN cos30°＝
（10－x）cm，………………………………………………1分
FD＝MG＝NH＝（10－x）cm，
∵AF＝x，且AF＋FD＝AD，
∴x＋（10－x）＝4，………………………1分
∴x1＝
＝
．………………………………………………………1分
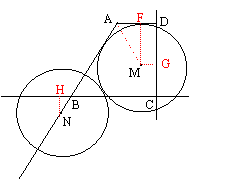又可能如图十六，NH＝BN cos30°＝（x－10）cm，
FD＝MG＝NH＝（x－10）cm，
∵AF＝x，且AF＋FD＝AD，
∴x＋（x－10）＝4，………………1分
∴x2＝＝
．………………………………………………………1分
因此，当x1＝．或x2＝时，直线CD被⊙M所截得的弦与直线BC被⊙N所截得的弦的长相等．