函数及其图象3课时

初三数学中考专题跟踪练习（五、函数及其图象3课时）

一、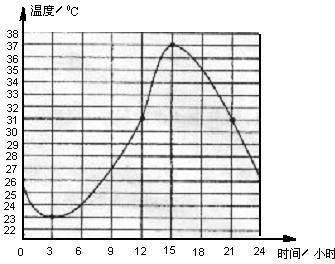填空题

1.　（海南03/17）用火柴棒按如图的方式搭一行三角形，搭一个三角形需3支火柴棒，搭2个三角形需5支火柴棒，搭3个三角形需7支火柴棒，照这样的规律搭下去，搭个三角形需要S支火柴棒，那么S关于的函数关系式是　　　　　　　　 (为正整数)

2.  （宁波03/12）已知抛物线经过点和，则的值是　　 。

3.　（杭州03改）把抛物线的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式是，则有b=　　　　 ，c=　　　　 。

4.　　 若一次函数的图象经过第一、二、四象限，则此函数的解析式为（写一个即可）： 　　　　　　　　　　　　　　

5.　试写出一个开口方向向上，对称轴为直线x = 2，且与y轴的交点坐标为(0,3)的抛物线的解析___________________________；

6.  （长沙03/24）如图：表示长沙市2003年6月份某一天的气温随时间变化的情况，请观察此图，回答下列问题：

（1）这天的最高气温是　　　　  度？

（2）这天共有　　　　  小时的气温在31度以上；

（3）这天有　　　　（时间）范围内温度在上升？

（4）请你预测一下，次日凌晨1点的气温是多少度？

　　　　  答：　　　　　　　　　　 。

二、 选择题

1.　　 （黄冈03/8）在直角坐标系中，点P（，）在第四象限，则的取值范围是（　　 ）A． 3＜＜5　 B．一3＜＜5 C． 一5＜＜ 3 D． 一5＜＜－3

2.　（哈尔滨03/6）若正比例函数的图像经过点A（，）和点B（，），当＜时＞，则的取值范围是（　　 ）

A．＜0　　　　　　　 B．＞0　　　　　　　　 C．＜　　　　　　　D．＞

3.　（桂林03/17）已知函数与的图像的交点在轴的负半轴上，那么的值为（　　）。A．±2 B．±4　C．2 D．－2

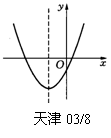
4.　（天津03/8）已知，如图为二次函数的图象，则一次函数的图象不经过第　（　　　）象限A．一 B．二　C．三 D．四

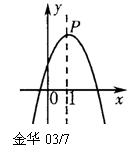
5.　　  （金华03/7）如图，抛物线顶点坐标是P（1，3），则函数y随自变量x的增大而减小的x的取值范围是（ 　）A．x＞3　　　　　　　　　　　　　　　 B．x＜3　C．x＞1　　　　　　　　　　　　　　　　　D．x＜1

6.　　　　 （宜昌03/10）函数y = kx + 1与函数在同一坐标系中的大致图象是（　　　）

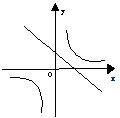
　　　A．　　　　　　　B．　　　　　　C．　　　　　　D．

7.　　　　 （广东03/2）如图，某个反比例函数的图像经过点P，则它的解析式（　　 ）

A．（＞0）　　　　　　　 　　　 B．（＞0）

C．（＜0　　　　　　　　　　　　　　　　　　　　　 D．（＜0

8.　　　　 （武汉03/28）一次函数y＝－kx＋4与反比例函数的图像有两个不同的交点，点（－，）、（－1，）、（，）是函数图像上的三个点，则、、的大小关系是（　　 ）

A．y₂＜y₃＜y₁　　　　　B．y₁＜y₂＜y₃ C．y₃＜y₁＜y₂　　 D．y₃＜y₂＜y₁．

三、简单解答题

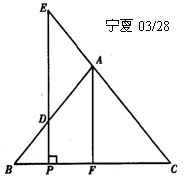
1.　　　　 （宁夏03/28）（10 分）如图，在△ABC中，AB＝AC＝5，BC＝6，F为BC的中点．P是BF上的一点，过点P作BC的垂线交AB于D，交CA的延长线于E．若设 BP＝x，那么，图中有些量（线段、面积等）可以看作x的函数，如，PC＝6－x，PF＝3－x等．除以上两例外，请你再写出一个关于x的函数解析式，并加以证明．（不要添加辅助线和其它字母）

2.　　  （上海03/23）已知：一条直线经过点A（0，4）、点B（2，0），如图，将这条直线向左平移与轴负半轴、轴负半轴分别交于点C．点D，使DB＝DC。求：以直线CD为图象的函数解析式。

3.　　　　 （厦门03/26）已知抛物线．（1）求证：此抛物线与x轴总有两个不同的交点；（2）设x₁、x₂是此抛物线与x轴两个交点的横坐标，且满足＝．　①求抛物线的解析式；②设点P（m₁，n₁）、Q（m₂，n₂）是抛物线上两个不同的点，且关于此抛物线的对称轴对称，求m₁＋m₂的值．

4.　　　　 （武汉03/40）已知：二次函数的图像与x轴交于A（，0）、B（，0），＜0＜，与y轴交于点C，且满足

⑴ 求这个二次函数的解析式；（5分）

⑵ 是否存在着直线y＝kx＋b与抛物线交于点P、Q，使y轴平分△CPQ的面积？若存在，求出k、b应满足的条件；若不存在，请说明理由．（5分）

5.　　　 （上海03/26）已知在平面直角坐标系内，O为坐标原点，A．B是轴正半轴上的两点，点A在点B的左侧，如图，二次函数（≠0）的图象经过点A．B，与轴相交于点C。　（1）、的符号之间有何关系？

　（2）如果线段OC的长度是线段OA．OB长度的比例中项，试证、互为倒数；

　（3）在（2）的条件下，如果＝－4，AB＝，求、的值。

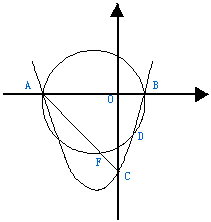
6.　　 如图，抛物线与x轴交于A．B两点，与y轴　交于点C，D是抛物线上一点，其坐标为()，B点坐标为(1,0)。⑴求抛物线的解析式；

⑵经过A．B．D三点的圆交AC于F，交直线y = x + 3于点E。试判断△ABC的形状，并加以证明。

7.　　　　 （广东03/20）某人从A城出发，前往离A城30千米的B城。现在有三种车供他选择：①自行车，其速度为15千米/时；②三轮车，其速度为10千米/时；③摩托车，其速度为40千米／小时。

（1）用哪些车能使他从A城到达B城的时间不超过2小时，请说明理由。

（2）设此人在行进途中离B城的路程为s千米，行进时间为小时，就（1）所选定的方案，试写出s与t的函数关系式（注明自变量t的取值范围），并在图7所给的平面直角坐标系中画出此函数的图像。