全国各地中考数学卷分类题解
函数及其图象
2004年北京升学
13.在函数y=中,自变量x的取值范围是________________.
16.我们学习过反比例函数.例如,当矩形面积S一定时,长a是宽b的反比例函数,其函数关系式可以写为a=(S为常数,S≠0).
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.
实例:______________________________________________________________________
__________________________________________________________________________;
函数关系式:_____________________________________________________________.
八、(本题满分8分)
25.已知:在平面直角坐标系xOy中,过点P(0,2)任作一条与抛物线y=ax2(a>0)交于两点的直线,设交点分别为A、B.若∠AOB=90°,
⑴ 判断A、B两点纵坐标的乘积是否为一个确定的值,并说明理由;
⑵ 确定抛物线y=ax2(a>0)的解析式;
⑶ 当ΔAOB的面积为4时,求直线AB的解析式.
郴州市2004年
12. 函数![]() 中,自变量x的取值范围是
(
)
中,自变量x的取值范围是
(
)
A. x < 1 B. x ≤ 1 C. x > 1 D. x ≥1
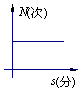
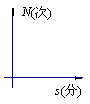
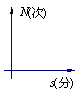
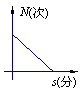 20. 一个正常人在做激烈运动时,心跳速度加快,当运动停止下来后,心跳次数N (次)与时间s(分)的函数关系图像大致是 ( )
20. 一个正常人在做激烈运动时,心跳速度加快,当运动停止下来后,心跳次数N (次)与时间s(分)的函数关系图像大致是 ( )
![]()
![]()
A B C D
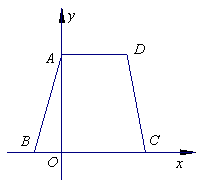 六、综合题(8分)26.已知:如图9,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=
六、综合题(8分)26.已知:如图9,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=![]() .
.
(1)求点B的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,
使得![]() ?若存在,请求出该点坐标,
?若存在,请求出该点坐标,
若不存在,请说明理由.
|
2004年大连市2、在平面直角坐标系中,点(-1,-2)所在的象限是 ( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限

6、如图2,直线![]() 与
与![]() 轴交于点(-4 , 0),则
轴交于点(-4 , 0),则![]() > 0时,
> 0时,
![]() 的取值范围是
(
)
的取值范围是
(
)
A、![]() >-4 B、
>-4 B、![]() >0
C、
>0
C、![]() <-4
D、
<-4
D、![]() <0
<0
9、函数![]() 中,自变量x的取值范围是___________________;
中,自变量x的取值范围是___________________;
12、大连市内与庄河两地之间的距离是160千米,若汽车以平均每小时80千米的速度从大连市内开往庄河,则汽车距庄河的路程y (千米)与行驶的时间x (小时)之间的函数关系式为_______________________________________;
15、反比例函数![]() 的图象经过点A(2 ,3),
的图象经过点A(2 ,3),
⑴求这个函数的解析式;
⑵请判断点B(1 ,6)是否在这个反比例函数的图象上,并说明理由。
四、解答题(本题共3小题,其中21题7分,22题8分,23题9分,共24分)
21、如图8,抛物线![]() 经过点A(1 ,0 ),与y轴交于点B。
经过点A(1 ,0 ),与y轴交于点B。
⑴求抛物线的解析式;
⑵P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标。

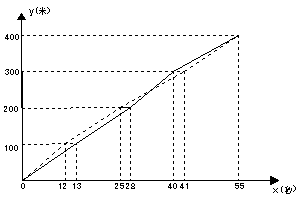 23、4×100米拉力赛是学校运动会最精彩的项目之一。图10中的实线和虚线分别是初三·一班和初三·班代表队在比赛时运动员所跑的路程y (米)与所用时间x (秒)的函数图象(假设每名运动员跑步速度不变,交接棒时间忽略不计)。
23、4×100米拉力赛是学校运动会最精彩的项目之一。图10中的实线和虚线分别是初三·一班和初三·班代表队在比赛时运动员所跑的路程y (米)与所用时间x (秒)的函数图象(假设每名运动员跑步速度不变,交接棒时间忽略不计)。
问题:
⑴初三·二班跑得最快的
是第_________接力棒的运动员;
⑵发令后经过多长时间两班运动员
第一次并列?
图10
 25、阅读材料,解答问题。
25、阅读材料,解答问题。
材料:“小聪设计的一个电子游戏是:一电子跳蚤从
这P1(-3 ,9)开始,按点的横坐标依次增加1的规律,
在抛物线![]() 上向右跳动,得到点
上向右跳动,得到点
P2、P3、P4、P5……(如图12所示)。过P1、P2、P3分别
作P1H1、P2H2、P3H3垂直于x轴,垂足为H1、H2、H3,则
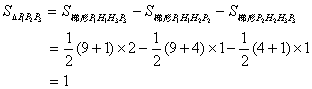
 即△P1P2P3的面积为1。”
即△P1P2P3的面积为1。”
问题:
⑴求四边形P1P2P3P4和P2P3P4P5的面积(要求:写
出其中一个四边形面积的求解过程,另一个直接写出答案);
⑵猜想四边形Pn-1PnPn+1Pn+2的面积,并说明理由(利用图13)
⑶若将抛物线![]() 改为抛物线
改为抛物线![]() ,其它
,其它
条件不变,猜想四边形Pn-1PnPn+1Pn+2的面积(直接写出答案)
云南省2004年
6、一组学生去春游,预计共需费用120元,后来又有2个参加进来,部费用不变,于是每人可少分摊3元,原来这组学生人数是( )
A、15人 B、 10人 C、 12人 D、8人
 7、若一次函数
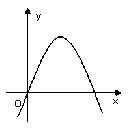
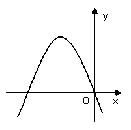
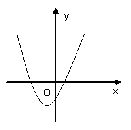
7、若一次函数![]() 的图象经过二、三、四象限,则二次函数
的图象经过二、三、四象限,则二次函数![]() 的图象只可能是( )
的图象只可能是( )
A、 B、 C、 D、
8、已知![]() 、
、![]() 、
、![]() 都是正数,且
都是正数,且![]() ,则下列四个点中,在正比例函数
,则下列四个点中,在正比例函数![]() 图象上的点的坐标是( )
图象上的点的坐标是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、如果![]() ,那么用
,那么用![]() 的代数式表示
的代数式表示![]() 为
;
为
;
19、(本小题满分7分)
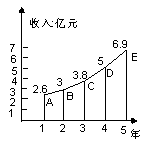
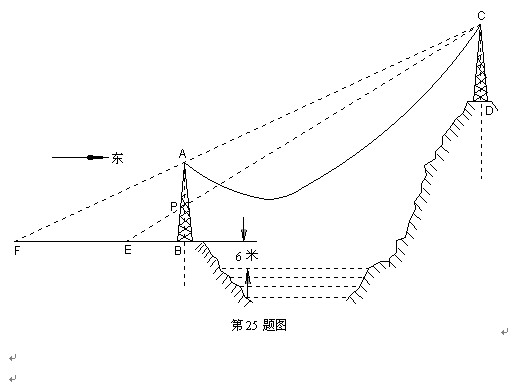
下图表示近5年来某市的财政收入情况。图中![]() 轴上1,2,…,5依次表示第1年,第2年,…,第5年,即1997年,1998年,…,2001年,可以看出,图中的折线近似于抛物线的一部分。
轴上1,2,…,5依次表示第1年,第2年,…,第5年,即1997年,1998年,…,2001年,可以看出,图中的折线近似于抛物线的一部分。
(1)请你求出过A、C、D三点的二次函数的解析式;
 (2)分别求出当
(2)分别求出当![]() 和
和![]() 时,(1)中的二次函数的函数值;并分别与B、E两点的纵坐标相比较;
时,(1)中的二次函数的函数值;并分别与B、E两点的纵坐标相比较;
(3)利用(1)中的二次函数的解析式预测今年该市的财政收入;
绍兴市2004年
3.函数![]() 的自变量x取值范围是( )
的自变量x取值范围是( )
A.x≥2 B.x>2 C.x≠2 D.x<2
4.已知正比例函数y=kx的图象经过点(1,2),则k的值为( )
A.![]() B.1
C.2 D.4
B.1
C.2 D.4
16.某城市自来水收费实行阶梯水价,收费标准如下表所示,用户5月份交水费45元,则所用水为 度.
| 月用水量 | 不超过12度的部分 | 超过12度不超过18度的部分 | 超过18度的部分 |
| 收费标准(元/度) | 2.00 | 2.50 | 3.00 |
泸州市2004年
14.抛物线![]() 的开口( )
的开口( )
A.向上 B.向下 C.不能确定 D.以上说法都不对
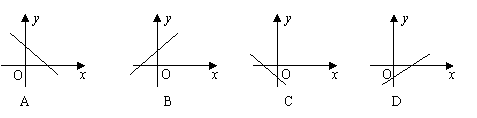 15.函数
15.函数![]() 的图象大致是( )
的图象大致是( )
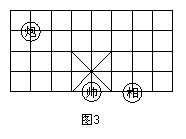 20.如图3所示的象棋盘上,若帅位于点(1,-2)上,相位于点(3,-2)上,则炮位于点( )
20.如图3所示的象棋盘上,若帅位于点(1,-2)上,相位于点(3,-2)上,则炮位于点( )
A. (-1,1) B. (-1,2)
C. (-2,1) D. (-2,2)
1.反比例函数![]() 经过点(1,3),则
经过点(1,3),则![]() ___.
___.
2.已知:![]() 、
、![]() 是方程
是方程![]() 的两根,则
的两根,则![]() =___.
=___.
3.牛顿发现“万有引力”定律据说来源于小时候在苹果树下看书,突然一个成熟的苹果掉下来正好落在他的头上,在疼痛这中,他想:为什么苹果往下掉,而不是“飞上天”呢?带着这样的疑问经过长期不断的学习、探索,终于发现了“万有引力”等定律,成为世界上著名的科学家这一。下面图象大致可反应苹果下落过程中速度V随时间t之间的变
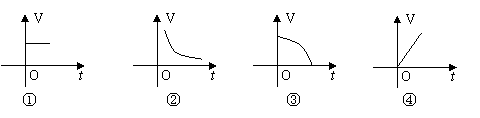 |
化情况的是___(填数字番号).
 |  | ||
4. 7.某企业在“蜀南竹海”收购毛竹进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元。由于受条件限制,每天只能采用一种方式加工,要求在一月内(30天)将这批毛竹全部销售。为此企业厂长召集职工开会,让职工讨论如何加工销售更合算?
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
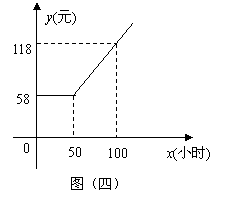
8.某广电局与长江证券公司联合推出广电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户交纳上网费的方式有:方式一,每月80元包干;方式二,每月上网时间x(小时)与上网费y(元)的函数关系用图(四)中的折线表示;方式三,以0小时为起点,每小时收费1.6元,月收费不超过120元。若设一用户每月上网x小时,月上网费为y元。
(1)根据图(四),写出方式二中y与x的函数关系式;
(2)试写出方式三中y与x的函数关系式;
(3)若此用户每月上网60小时,选用哪种方式上网,其费用最少?最少费用是多少?
 |
长春市2004年 6.反比例函数
![]() 的图像在______象限.
的图像在______象限.
14.一次函数y=ax+b的图像如图所示,则下面结论中正确的是( )
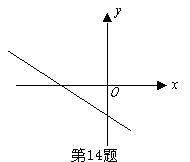
A.a<0,b<0 B.a<0,b>0
C.a>0,b>0 D.a>0,b<0
22.已知正比例函数 ![]() 的图像与一次函数
的图像与一次函数
![]() 的图像交于点P(3,-6).
的图像交于点P(3,-6).
(1)求k1、k2的值;
(2)如果一次函数 ![]() 的图像与x轴交于点A,求点A的坐标.
的图像与x轴交于点A,求点A的坐标.
北京市丰台区2004年 12. 在直角坐标系中,点P(1,-1)一定在( )
A. 抛物线![]() 上
B. 双曲线
上
B. 双曲线![]() 上
上
C. 直线![]() 上
D. 直线
上
D. 直线 ![]() 上
上
16. 如果b>0,c>0,那么二次函数![]() 的图象大致是( )
的图象大致是( )
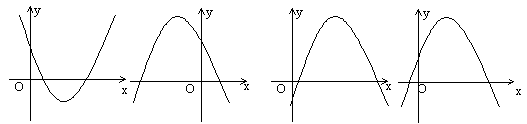
A. B. C. D.
北京市东城区2004年
2.抛物线![]() 的顶点坐标是( )
的顶点坐标是( )
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
10.如果反比例函数![]() 在其象限内,y随x的增大而减小,那么它的图象分布在( )
在其象限内,y随x的增大而减小,那么它的图象分布在( )
A.第一、二象限 B. 第一、三象限 C. 第二、三象限 D. 第二、四象限
11.函数![]() 的自变量x的取值范围是( )
的自变量x的取值范围是( )
A.x>2 B.x≤2 C.x<2 D. x<2且x≠0
17.直线![]() 不经过第___象限.
不经过第___象限.
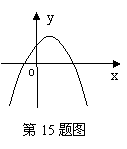 15.已知二次函数
15.已知二次函数![]() 的图象如图所示,则下列结论正确的是( )
的图象如图所示,则下列结论正确的是( )
A.![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
2004杭州
24. (本小题满分10分)
某航运公司年初用120万元购进一艘运输船,在投入运输后,每一年的总收入为72万元,需要支出的各种费用为40万元。
(1)问:该船运输几年后开始盈利(盈利即指总收入减去购船费及所有支出费用之差为正值)?
(2)若该船运输满15年要报废,报废时旧船卖出可收回20万元,求这15年的年平均盈利额(精确到0.1万元)。
25. (本小题满分10分)
二次函数![]() 的图象的一部分如右图,已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)。
的图象的一部分如右图,已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)。
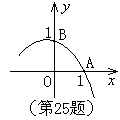 (1)请判断实数
(1)请判断实数![]() 的取值范围,并说明理由;
的取值范围,并说明理由;
(2)设此二次函数的图象与![]() 轴的另一个交点为C,当ΔAMC的面积为ΔABC面积的
轴的另一个交点为C,当ΔAMC的面积为ΔABC面积的![]() 倍时,求
倍时,求![]() 的值。
的值。
15. 甲、乙两人连续7年调查某县养鸡业的情况,提供了两方面的信息图(如图)。
甲调查表明:养鸡场的平均产鸡数从第1年的1万只上升到第7年的2.8万只;
乙调查表明:养鸡场的个数由第1年的46个减少到第7年的22个。
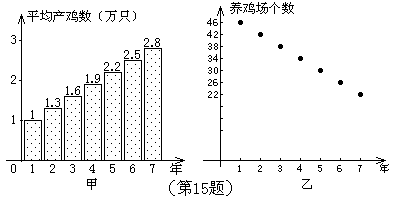
现给出下列四个判断:①该县第2年养鸡场产鸡的数量为1.3万只;②该县第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量;③该县这7年养鸡场产鸡的数量逐年增长;④这7年中,第5年该县养鸡场出产鸡的数量最多。根据甲、乙两人提供的信息,可知其中正确的判断有
(A)3个 (B)2个 (C)1个 (D)0个
2004河南
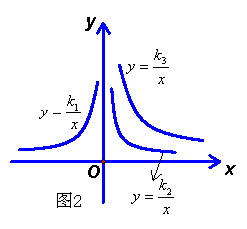 4.如图2是三个反比例函数
4.如图2是三个反比例函数![]() 在x轴上方的图象,由此观察得到
在x轴上方的图象,由此观察得到![]() 的大小关系为【 】
的大小关系为【 】
A.![]() >
>![]() >
>![]()
B.![]() >
>![]() >
>![]()
C.![]() >
>![]() >
>![]()
D.![]() >
>![]() >
>![]()
18.人在运动时的心跳速率通常和人的年龄有关.如果用a表示一个人的年龄,用b表示正常情况下这个人运动时所能承受的每分心跳的最高次数,那么b=0.8 (220-a).
(1)正常情况下,在运动时一个16岁的学生所能承受的每分心跳的最高次数是多少?
(2)一个50岁的人在运动时10秒心跳的次数为20次,他有危险吗?
23.某市今年来经济发展速度很快,根据统计:该市国内生产总值1990年为8.6亿元人民币,1995年为10.4亿元人民币.
经论证,上述数据适合一个二次函数关系.请根据这个函数关系,预测2005年该市国内生产总值将达到多少?
2004年锦州
10.苹果熟了,从树上落下所经过的路程s与下落的时间t满足s=![]() gt2(g是不为0的常数),则s与t的函数图象大致是( )
gt2(g是不为0的常数),则s与t的函数图象大致是( )
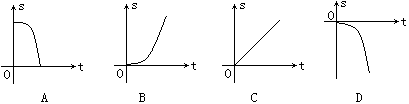
14.若点A(2,m)在函数y=x2-1的图象上,则点A关于x轴的对称点的坐标是_____.
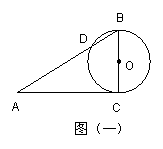
17.如图,点A在反比例函数y=![]() 的图象上,AB垂直于x轴,若S△AOB=4,那么这个反比例函数的解析式为_____.
的图象上,AB垂直于x轴,若S△AOB=4,那么这个反比例函数的解析式为_____.
22.某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年这种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线(部分)表示这种蔬菜销售价与月份之间的关系.观察图象,你能得到关于这种蔬菜销售情况的哪些信息?
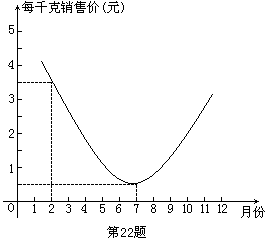
答题要求:(1)请提供四条信息;(2)不必求函数的解析式.
26.某食品批发部准备用10000元从厂家购进一批出厂价分别为16元和20元的甲、乙两种酸奶,然后将甲、乙两种酸奶分别加价20%和25%向外销售.如果设购进甲种酸奶为x(箱),全部售出这批酸奶所获销售利润为y(元).
(1)求所获销售利润y(元)与x(箱)之间的函数关系式;
(2)根据市场调查,甲、乙两种酸奶在保质期内销售量都不超过300箱,那么食品批发部怎样进货获利最大,最大销售利润是多少?
2004年辽宁省
2004浙江金华
1. (9分)已知x1、x2是关于x的方程x2-2x+t+2=0的两个不相等的实数根。
(1)求t的取值范围;(2)设S= x1+x2,求S关于t的函数关系式。
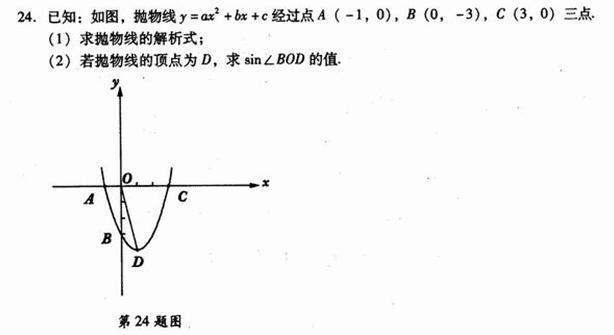
 22.(9分)如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点。(1)求此抛物线的解析式;(2)如果点D(1,m)在这条抛物线上,求m的值的点D关于这条抛物线对称轴的的对称点E的坐标,并求出tan∠ADE的值。
22.(9分)如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点。(1)求此抛物线的解析式;(2)如果点D(1,m)在这条抛物线上,求m的值的点D关于这条抛物线对称轴的的对称点E的坐标,并求出tan∠ADE的值。


2004年厦门
18、(本题满分10分)
(1) 甲品牌拖拉机开始工作时,油箱中有油30升.如果每小时耗油6
升,求油箱中的余油量y(升)与工作时间x(时)之间的函数关系式.
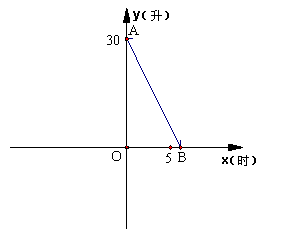 (2) 如图,线段AB表示乙品牌拖拉机在工作时油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象. 若甲、乙两种品牌的拖拉机在售价、质量、
(2) 如图,线段AB表示乙品牌拖拉机在工作时油箱中的余油量y(升)与工作时间x(时)之间的函数关系的图象. 若甲、乙两种品牌的拖拉机在售价、质量、
性能、售后服务等条件上都一样.根据图象提供的信息,你愿意
购买哪种品牌的拖拉机,并说明理由.
27、(本题满分10分)
已知抛物线y=ax2+(b-1)x+2.
(1)若抛物线经过点(1,4)、(-1,-2), 求此抛物线的解析式;
(2) 若此抛物线与直线y=x有两个不同的交点P、Q,且点P、Q关于原点对称.
① 求b的值;
② 请在横线上填上一个符合条件的a的值: a = ,并在此条件下画出该函数的图象.
2004龙岩
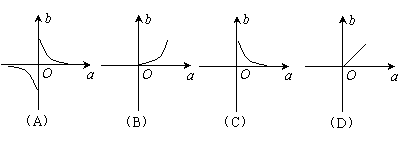
14. 若矩形的面积S为定值,矩形的长为a,宽为b,则b关于a的函数图象大致是
22. (10分)为加强公民节约用水,减少污水排放的环保意识,某城市制定了以下用水收费标准(含城市污水处理费):每户每月用水未超过8 m3时,按1.2元/ m3收费;每户每月用水超过8 m3时,其中的8 m3仍按原标准收费,超过部分按1.9元/m3收费.设某户每月用水量为x(m3),应交水费为y(元).
(1)分别写出用水未超过8m3和超过8m3时,y与x之间的函数关系式;
(2)某用户五月份共交水费13.4元,问该用户五月份用水多少m3.
2004福州

2004福州新校区
(五)(本题9分)
某工厂设门市部专卖某产品,该产品每件成本40元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
| 每件销售价(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
| 每天售出件数 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设当天定的售价是不变的,且每天销售情况均服从这种规律。
(1)观察这些统计数据,找出每天售出件数![]() 与每件售价
与每件售价![]() (元)之间的函数关系,并写出该函数关系式。
(元)之间的函数关系,并写出该函数关系式。
(2)门市部原设有两名营业员,但当销售量较大时,在每天售出量超过168件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为40元。
求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)
2004富阳
33、已知一个长方体的木箱高为80![]() ,底面的长比宽多10
,底面的长比宽多10![]() ,(1)求这个长方体的体积
,(1)求这个长方体的体积![]() (
(![]() )与长方体的宽
)与长方体的宽![]() (
(![]() )之间的函数关系式;(2)问当该木箱的体积为0.72
)之间的函数关系式;(2)问当该木箱的体积为0.72![]() 时,木箱底面的长与宽各为多少
时,木箱底面的长与宽各为多少![]() ?
?
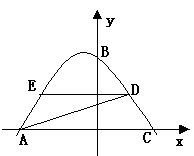
34、(8分)已知一个二次函数的图象经过A(-1,0),B(0,3),C(4,-5)三点.(1)求这个函数的解析式及其顶点D的坐标; (2)这个函数的图象与![]() 轴有两个交点,除点A外的另一个交点设为E,点O为坐标原点,在△AOB、△BOE、△ABE和△DBE这四个三角形中,是否有相似三角形?如果有,指出哪几对三角形相似,并加以证明;如果没有,请说明理由。
轴有两个交点,除点A外的另一个交点设为E,点O为坐标原点,在△AOB、△BOE、△ABE和△DBE这四个三角形中,是否有相似三角形?如果有,指出哪几对三角形相似,并加以证明;如果没有,请说明理由。