和圆有关的比例线段

和圆有关的比例线段

 

【同步达纲练习】(时间：45分钟，满分：100分)

一、填空题(8分×5=40分)

(1)⊙O内弦CD垂直于直径AB，E为垂足，且AE=4cm，BE=9cm，CD=_4　_.

(2)圆内两相交弦，一弦长3cm被交点平分，另一弦被交点分成1：4，则此弦长为______.

(3)已知圆的切线PT的长是6cm，割线PAB的长是9cm，则弦AB的长是______.

(4)在直径为2的圆外有一点P到圆的最近点的距离为3，则过这点的切线长是______.

(5)⊙O的割线PAB交⊙O于A、B两点，已知：PA=6cm,AB=7cm,PO=12cm,则⊙O的半径为______.

 

二、选择题(8分×5=40分)

(1)圆的两弦相交，一弦被分为12cm和8cm两段，另一弦被分为3：8，则另一弦长是(　　)

A．11cm　　　　　 B.9 cm　　　　　  C.22cm　　　　　  D.33cm

(2)圆内接正方形ABCD的边长为2,弦AK平分边BC,则AK的长为(　　)

A.　　　　　  B.　　　　  C.　　　　　　 D.

(3)从圆外一点向半径为9的圆作切线,已知切线长为18,则从这一点到圆的最短距离是(　　)

A.9　　　　　　 B.9-9　　　　C.9-9　　　　　 D.9

(4)已知⊙O外一定点P,P与O的距离为4cm,从P点向圆作切线,切线长与圆的半径之差为2cm,则圆的半径为(　　)

A.(1+)cm　　　　　　　　　　  B.(-1)cm或(1+)cm

C.(-1)cm或(1+)cm　　　　  D.(-1)cm

(5)已知PA是圆的切线,A为切点,PBC是圆的割线,与圆相交于B、C两点,若PB=3,BC=6,则PA的长为(　　)

A.6　　　　　　　 B.2　　　　　 C.3　　　　　 D.3

 

三、解答题：(10分×2=20分)

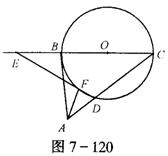
(1)如图7-120，BC是⊙O的直径，AB是⊙O的切线，B是切点，AB=BC，AC交⊙O于

D，E在CB的延长线上，BE=BC，DE交⊙O于F，求证AF⊥DE.

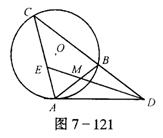
(2)如图7-121,M为弦AB的中点,C为圆上任意一点,切线AD交CB的延长线于D,连DM并延长交AC于E,求证AD²:BD²=CE:AE.

 

【素质优化训练】

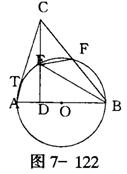
1.如图7-122,AB是⊙O的直径,CD⊥AB于D,CT切⊙O于T,求证:BE²+CT²=BC².

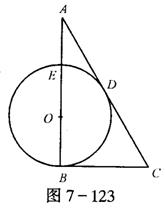
2.如图7-123,已知CB、CD切⊙O于B、D点,过B作直径交⊙O于E交CD的延长线于A,若AD=m·AE,且tg=,求m的值.

 

 

参考答案

【同步达纲练习】

一、(1)12cm　 (2)cm　 (3)5cm　 (4)　　(5)8cm

二、C　 B　 C　 C　 C

三、(1)连AE，△AEC为Rt△, AE²=EB·EC=EF·ED，∴AF⊥DE

(2)过B作BF∥DE交AC于F，则：AD²：BD²=CD：BD=CE：EF=CE：AE

 

【素质优化训练】

1．连AE、AF，则∠AEB=90°，△ABE ∽△EBD，∴BE²=AB·BD，又△AFB∽△CDB，∴AB·DB=BC·BF，∴BE²=BC·BF，又CT²=CF·BC，∴BE²+TC²=BC·BF+BC·CF=BC²

2．连OD、OC则：∠BCO=∠DCO=∠C，∵tg= ,= ,再证△ADO∽△ACB，∴ ，又∵OD=OB，∴，∴AB=3AD，由切割线定理知：AD²=AE· AB=AE· 3AD，  ∴AD=3AE，∴m=3