精华培训学校初三特训班数学测试题2（海淀）
（测试时间30分钟）
姓名 班级 学号 分数
一、填空题
1．二次函数
的图象在x轴上截得线段长为 。
2．若抛物线y＝x2＋bx＋8的顶点在x轴的正半轴上，则b的值为 。
3．二次函数y＝ax2＋bx＋c中，若a∶b∶c＝1∶4∶3，且该函数的最小值是－3，则解析式为 。
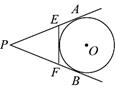4．如图，PA、PB分别与圆O相切于A、B两点，EF与圆O
相切于M，若PA长为2，则∆PEF的周长是 。
5．∆ABC内接于圆O，且AB＝AC，圆O的半径等于6cm，O点
到BC距离等于2cm，则AB长为 。
6．圆O是∆ABC的内切圆，∠C＝90°，∠BOC＝105°，BC＝20cm，则AC长为 。
二、选择题
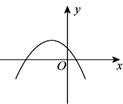
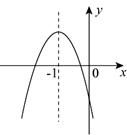
1．设二次函数y＝－x2＋(m－2)x＋3 (m＋1)的图象如图所示，则m的取值范围是（ ）
A．m＞－1
B．m＜2
C．－1＜m＜2
D．m＜－1或m＞2
2．两圆的直径分别为8cm、6cm，一条外公切线长为8cm，则这两个圆的位置关系是（ ）
A．外离 B．内切 C．外切 D．相交
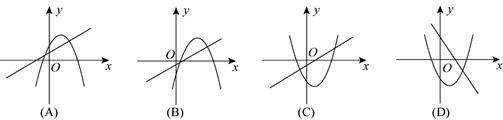
3．当b＜0时，一次函数y＝ax＋b和二次函数y＝ax2＋bx＋c在同一坐标系内图象可能是下面四个图中的（ ）
 |
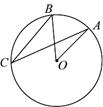
4．如图，A、B、C是圆O上三点，
的度数是50°，∠OBC＝40°，∠OAC等于（ ）
A．15°
B．25°
C．30°
D．40°
5．在∆ABC中，∠C＝90°，O是BC上一点，以OB为半径作圆O交AB于D，交AC于E，若∠A＝30°，BD＝6cm，则圆O的半径为（ ）
A．6cm B．12cm C．9cm D．3cm
6．y＝ax2＋bx＋c（a≠0）的图象如图所示，则下面六个代数式：abc；b2－4ac；a－b＋c；a＋b＋c；2a－b；9a－4b，值小于0的有（ ）
A．1个
B．2个
C．3个
D．4个
三、解答题
1．已知抛物线
与x轴交于不同的两点A（x1，0），B（x2，0），点A在点B的左边，抛物线与y轴交于点C，若A、B两点位于y轴异侧，且
，求抛物线的解析式。
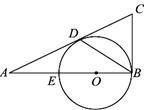2．已知：如图，Rt∆ABC，∠ABC＝90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于E，与AC切于D，且AD＝2，AE＝1。
求：（1）圆O直径的长
（2）BC的长
（3）sin∠DBA的值
精华培训学校初三特训班数学测试题答案（海淀）
一、填空题
1．6 2．
3．y＝3x2＋12x＋9
4．4 5．
6．
二、选择题
1．C 2．A 3．C 4．A 5．A 6．C
三、解答题
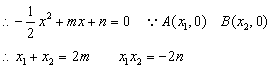1．解：∵图象与x轴有交点，∴令y＝0
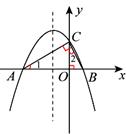
∵图象与y轴有交点，∴令x＝0
∴y＝n ∴C (0，n)
 |
∵∠ACB＝90°，CO⊥x轴 ∴OC2＝AO·OB
∵A、B两点在y轴异侧， ∴OA＝－x1，OB＝x2
即n2＝－(－2n) ∵n≠0 ∴n＝2 ∴OC＝2
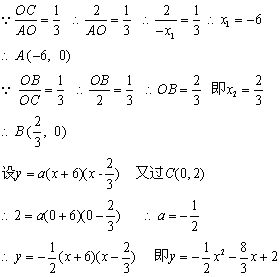
2．解：（1）∵AD是圆O的切线，AB是圆O的割线
∴AD2＝AE（AE＋EB）
即4＝1·（1＋BE）∴BE＝3，即圆O的直径长。
（2）∵OB是圆O的半径，且∠ABC＝90°，∴BC是圆O的切线
∵CD是圆O的切线 ∴DC＝BC 设BC＝x
Rt∆ABC x2＋42＝(2＋x)2 解之x＝3 即BC＝3
（3）连结DE，可证∆ADE∽∆ABD
 |
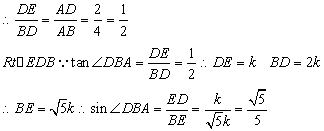