初三外省市招生数学试卷（第一次）
（本试卷满分100分，90分钟完成）
一、单项选择题：（本大题满分30分）本大题共有10个小题，每小题给出了代号为(A)、(B)、(C)、(D)四个答案，其中有且只有一个答案是正确的。请把正确答案的代号写在题后的圆括号内。每小题选对得3分；不选、错选或选出的代表字母超过一个（不论是否写在圆括号内），一律得零分。
1、
计算：
，得 ( D )
(A) 
(B) 1 (C) 
(D) 
2、 如果a>b，那么下列结论正确的是 ( B )
(A) ac2>bc2 (B) 3-a<4-b (C) a-3>b-2 (D) 
3、 已知等腰梯形的中位线长为12，一条对角线分中位线所成的两条线段之比是2∶1，则梯形的两底长分别为 ( A )
(A) 8，16 (B) 10，14 (C) 6，18 (D) 4，20
4、 如果两圆的公切线只有两条，那么这两个圆的位置关系是 ( A )
(A) 相交 (B) 外离 (C) 内切 (D) 外切
5、 设f(x)=x2-2004x+2004，（f(x)表示关于x的函数，如f(0)=02+2004·0+2004=2004，f(m)=m2-2004m+2004）若f(m)=f(n)，则f(m+n)= ( B )
(A) 0 (B) 2004 (C) -2004 (D) 1002
6、 若三角形的三个内角A、B、C的关系满足A>3B，C<2B，那么这个三角形是 ( A )
(A) 钝角三角形 (B) 直角三角形 (C) 等边三角形 (D) 非等边的锐角三角形
7、
如果∠A是锐角，且sinA=
，那么 ( C )
(A) 0°<∠A<30° (B) 30°<∠A<45° (C) 45°<∠A<60° (D) 60°<∠A<90°
8、
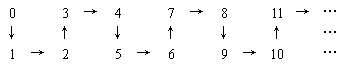观察右图，根据规律，从2002到2004，箭头方向依次为
(A) ↓→ (B) →↑ (C) ↑→ (D) →↓ ( C )
9、 已知一组数据6，8，10，x的中位数与平均数相等，这样x的有( C )
(A) 1个 (B) 2个 (C) 3个 (D) 4个以上（含4个）
10、 点P是矩形ABCD内一点，如果PA=3，PB=4，PC=5，则PD的长度是
(A) 
(B) 5
(C) 2
(D) 3 ( D )
二、填空题：（本大题满分36分）本大题共有12个小题，各小题只要求在横线上方填写最终、最准确的结果，每题填写正确得3分，否则一律得0分。
11、
若实数x满足
，则x5+x+2的值为____1___。
12、 在△ABC中，∠C=90°，如果
，那么∠B的余切cotB=__________。
13、
若方程│x2-1│=x+k恰有三解（相等实根算一解），则k的值是_1或
___。
14、 把抛物线y=-3(x-2)2向上平移k个单位，所得抛物线与x轴交于点A（x1，0）与B（x2，0），如果
，那么k的值为_____3______。
15、
某养鱼户为了估计鱼塘内鱼的条数和重量，先网出100条鱼，做上标记后全部放回鱼塘，过些时候捕捞出90条鱼，发现其中有4条鱼带有标记，估计该鱼塘内养鱼约有___2250___条。
16、 如图，四边形ABCD中，∠ADC和∠ABC都是直角，DE垂直于AB，AD边与CD边长度相等。已知四边形ABCD的面积为16，那么线段DE的长度是__4__。
17、 在△ABC中，D为BC的中点，E为AD的中点，如果延长BE交AC于F，那么AF∶FC=__1∶2___。
18、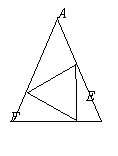 
如图，△ABC中，已知AB=AC，△DEF是△ABC的内接正三角形，α=∠BDF，β=∠CED，γ=∠AFE，则用β、γ表示α的关系式是____
_____。
19、 若扇形的圆心角是60°，则该扇形面积与其内切圆面积的比值是___3∶2_____。
20、 有红、白、绿、兰4种颜色的袜子各100只，在黑暗中至少要摸出__39____只袜子，才能保证摸出的袜子至少有18双（每两只同色袜子叫做一双）。
21、 在数集上定义运算a⊕b，规则是：当a≥b时，a⊕b=b3；当a<b时，a⊕b=b2。根据这个规则，方程4⊕x=64的解是___4或8___。
22、 小于1000的自然数中，不能被5和7整除的数有__686__个。
三、解答题：（本大题满分34分）本大题共3题，解答下列各题必须写出必要的步骤。
23、 （本题满分10分）本题共有3个小题，第1小题满分3分，第2小题满分3分，第3小题满分4分。
如图，在Rt△ABC中，∠ABC=90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，且AD=2，AE=1。求：
（1）⊙O的直径的长；
（2）求BC的长；
（3）求∠DBA的正切tan∠DBA。
解：设⊙O的半径为r，
（1）由切割线定理，得AE·AB=AD2，即1·(1+2r)=22=4。
∴2r=3，∴⊙O的直径为3。
（2）易有，△ODA∽△CBA，∴
，∴BC=
=
=3。
（3）tan∠DBA=tan∠OCB=
=
=
。▋
24、 （本题满分12分）本题共有3个小题，第1小题满分4分，第2小题满分4分，第3小题满分4分。
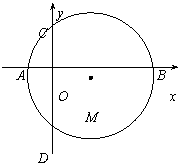已知圆M与x轴交于A、B两点，与y轴交于C、D两点，若A、B、C三点的坐标分别是A(-2，0)、B(12，0)、C(0，4)，
（1）求点D的坐标；
（2）求圆心M的坐标；
（3）若一抛物线过A、B、C，另一抛物线过A、B、D，求两条抛物线顶点间的距离。
解：（1）根据相交弦定理，OA·OB=OC·OD，
∴OD=
=
=6，
∴点D的坐标为(0，-6)。
（2）x=
=5，y=
=-1。
∴圆心M的坐标为(5，-1)。
（3）设过A、B两点的抛物线方程为y=a(x+2)(x-12)，
∵抛物线y=a1(x+2)(x-12)过点C(0，4)，∴a1=
=
，
∴过A、B、C三点的抛物线为y=(x+2)(x-12)；
∵抛物线y=a2(x+2)(x-12)过点D(0，-6)，∴a2=
=
，
∴过A、B、D三点的抛物线为y=(x+2)(x-12)；
∵它们的顶点的横坐标都为5，
∴两条抛物线顶点间的距离
d=∣(5+2)(5-12)-(5+2)(5-12)∣=(+
)·7·7=
。▋
25、 （本题满分12分）
求证：不存在这样的正整数，把它的首位数字移到末位之后，得到的数是原来数的两倍。
证明：假设存在这样的数，设它的首位数字为A（0<A<10）。
则该数可写成：A·10k+x（0<x<10k）。
∴2(A·10k+x)=x·10+A，∴8x=(2·10k-1)·A。
∵(8，2·10k-1)=1，∴8│A，又∵0<A<10，∴A=8。
∴x=2·10k-1，与0<x<10k矛盾。
∴没有满足要求的整数。▋