初中毕业、升学数学考试
本试卷分1、2两卷，其中1卷100分，2卷70分．考试时间120分钟．
1 卷
一、选择题（本大题共10题，每题只有一个正确答案，每题4分，共40分）
1．中央电视台新闻报道：国家财政部设立专项基金20个亿（人民币），用于“非典型性肺炎”的防治工作．用科学记数法可表示为（ ）元．
（A）0.2
（B）2
（C）2
（D）20
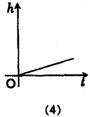
2．已知：如图，小明在打网球时，要使球恰好能打过网，而且落在离网5米的位置上，则球拍击球的高度h应为( )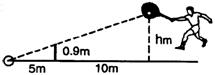 
（A）2.7m （B）1.8m （C）0.9m （D）6m
3．∵
……………………①
……………………②
∴
……………………………………③
∴2＝－2……………………………………………④
以上推导中的错误在第（ ）步．
（A）①（B）②（C）③（D）④
4． 已知：如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC＝30°，则∠CAD等于（ ）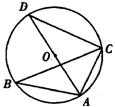
（A）30°（B）40°（C）50°（D）60°
5．200年2月24日，新疆伽师、巴楚发生6.8级的强烈地震．如图，若以乌鲁木齐为坐标原点建立平面直角坐标系，则震中应位于（ ）
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
6．以下各组字母和汉字中，既是轴对称又是中心对称的一组是（ ）
（A）W．O．E．申 （B）A．M．O．干 （C）H．O．X．田 （D）N．H．O．中
7．下列函数中，图像一定经过原点的函数是（ ）
（A）y＝3x－2 （B）
（C）
（D）
8．某人到瓷砖商店去购买一种正多边形形状的瓷砖，铺设无缝地板，他购买的瓷砖形状不可以是（ ）
（A）正三角形 （B）正四边形 （C）正六边形 （D）正八边形
9．某种冰淇淋纸筒为圆锥形，其底面半径为3cm，母线长为8cm，则制作这种纸筒所需纸片的面积（不计加工余料）为（ ）
（A）24π
（B）48π（C）30π（D）36π
10．一班学生检查视力，结果如下：
从上述数据上看出，全班视力数据的众数是（ ）
（A）0.9（B）1.0（C）20％（D）65％
二、填空题（本大题共5题，每题4分，共20分）
11．右图是由16个边长为1的小正方形拼成的，任意连结这些小正方形的若干个顶点，可得到一些线段，试分别画出一条长度是有理数的线段和一条长度是无理数的线段．
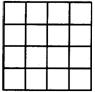
12．自行车在同一平面内两个圆形车轮的公切线有 条。
13．不解方程，判别方程5（
－1）－x＝0的根的情况是
。
14．乌鲁木齐至库尔勒的铁路长约600千米，火车从乌鲁木齐出发，其平均速度为58千米/小时，则火车离库尔勒的距离S（千米）与行驶时间t（小时）的函数关系式是 。
15．在△ABC和△ADC中，下列三个论断①AB＝AD、②∠BAC＝∠DAC、③BC＝DC，将其中的两个论断作为条件，另一个论断作为结论写出一个真命题 。
三、解答题（本大题共5题．每题8分，共40分）
16．用配方法解方程 
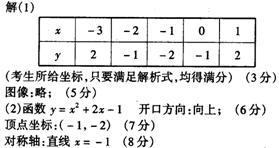
17．已知二次函数
（1）求出函数图像上5个点的坐标，并画出函数的图像；
（2）指出该函数的开口方向，顶点坐标及对称轴。
解：（1）列表
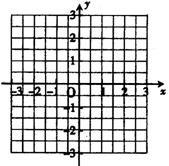
（2）
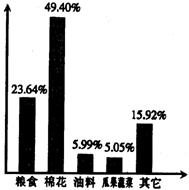
18．已知：下图是兵团2001年农作物种植面积分布统计图（数据来源：《兵团2002年统计年鉴》）．
（1）图中各个小长方形的面积分别表示什么？所有小长方形的面积之和等于多少？
（2）已知2001年农作物种植总面积为916.25千公顷，请你算出图中各类作物的种植面积（保留四位有效数字）．
19．已知：如图，AB是⊙O的直径，CD是弦，AE⊥CD，垂足是E，BF⊥CD，垂足是F，求证：CE＝DF．小明同学是这样证明的：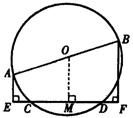
证明：∵ OM⊥CD
订正：
？
∴ CM＝MD
∵ AE∥OM∥BF
？
∴ ME＝MF
？
∴ ME－CM＝MF－MD
即 CE＝DF
横线及问号是老师给他的批注，老师还写了如下评语：“你的解题思路很清晰．但证明过程欠完整，相信你再思考一下，一定能写出完整的证明过程”．请你帮助小明订正此题，好吗？
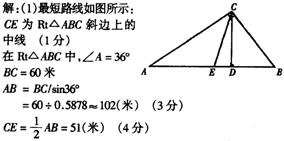
20. 某校把一块形状相似于直角三角形的废地开辟为生物园，如图所示，∠ACB＝90°、BC＝60米、∠A＝36°．
（1）若入口E在边AB上，且与A、B等距离，请你在图中画出入口E到C点的最短路线，并求出最短路线CE的长（保留整数）．
（2）若线段CD是一条水渠，并且D点在边AB上，已知水渠造价为50元/米；水渠路线应如何设计才能使造价最低，请你画出水渠路线，并求出最低造价．
2卷
一、填空题（本大题有5题、每题4分．共20分）
21. 已知方程
的两根的倒数和是
，则k＝ 。
22．请你写出函数
与
具有的一个共同性质 。
23．为估计新疆巴音布鲁克草原天鹅湖中天鹅的数量，先捕捉10只，全部做上标记后放飞；过一段时间后，重新捕捉40只，数一数带有标记的天鹅有2只．据此可估算出该地区大约有天鹅 只。
24．在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻，当甲带球冲到A点时，乙已跟随冲到B点．从数学角度看，此时甲是自己射门好，还是将球传给乙，让乙射门好？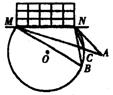
答： 简述理由：
。
25．四个容量相等的容器形状如下：
（A） （B） （C）
（D）
以同一流量的水管分别注水到这四个容器，所需时间都相同，下列图像显示注水时，容器水位（h）与时间（t）的关系． 请把适当的图像序号与相应容器形状的字母代号用线段相连接．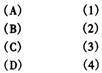
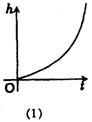
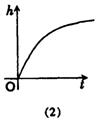
二、解答题（本大题共5题，第26、28、30题每题10分，第27题12分，第29题8分，共50分）
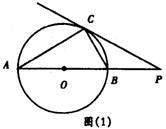
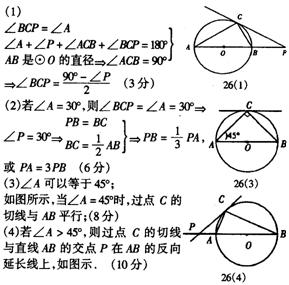
26．已知：如图（1），点P在⊙O外，PC是⊙O的切线、切点为C，直线PO与⊙O相交于点A、B．
（1）试探求∠BCP与∠P的数量关系；
（2）若∠A＝30°，则PB与PA有什么数量关系？
（3）∠A可能等于45°吗？若∠A＝45°，则过点C的切线与AB有怎样的位置关系？（图（2）供你解题使用）
（4）若∠A＞45°，则过点c的切线与直线AB的交点P的位置将在哪里？（图（3）供你解题使用）
27. 二次函数
的图像与x轴交于B、C两点，与y轴交于A点．
（1）根据图像确定a、b、c的符号，并说明理由；
（2）如果点A的坐标为（0，－3），∠ABC＝45°，∠ACB＝60°，求这个二次函数的解析式．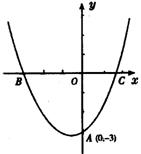
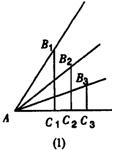
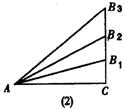
28．（1）如图（1）、（2），锐角的正弦值和余弦值都随着锐角的确定而确定，变化而变化．试探索随着锐角度数的增大．它的正弦值和余弦值变化的规律．
（2）根据你探索到的规律，试比较18°，34°，50°，62°，88°，这些锐角的正弦值的大小和余弦值的大小。
（3）比较大小（在空格处填写“＜”，或“＞”，或“＝” 号）：
若a＝45°，则sinα cosα；若α＜45°，则sinα cosα；
若α＞45°，则sinα cosα。
（4）利用互为余角的两个角的正弦和余弦的关系，试比较下列正弦值和余弦值的大小．sin10° 、cos30°、sin50° 、cos70°
29. 已知：如图，正方形ABCD的周长为4a，四边形EFGH的四个顶点E、F、G、H分别在AB、BC、CD、DA上滑动，在滑动过程中，始终有EH∥BD∥FG，且EH＝FG，那么四边形EFGH的周长是否可求？若能求出，它的周长是多少？若不能求出，请说明理由．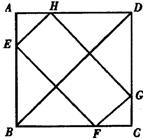
30．一位投资者有两种选择：①中国银行发行五年期国债，年利率为2．63％．②中国人寿保险公司乌鲁木齐市分公司推出的一种保险一一鸿泰分红保险，投资者一次性交保费10000元（10份），保险期为5年，5年后可得本息和10489.60元，一般还可再分得一些红利，但分红的金额不固定，有时可能多，有时可能少．
（1）写出购买国债的金额x（元）与5年后银行支付的本息和
（元）的函数关系式；
（2）求鸿泰分红保险的年利率，并写出支付保费x（元）与5年后保险公司还付的本息和
（元）的函数关系式（红利除外）；
（3）请你帮助投资者分析两种投资的利弊．
答案：
16..
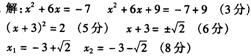
17.
18.
(1)图中各小长方形的面积分别表示该种农作物占种植总面积的百分比；（答百分率，频率均可）（2分）所有小长方形的面积之和等于1（或100％）．（3分）
(2)粮食种植面积约为216．6千公顷；（4分）
棉花种植面积约为452．6千公顷；（5分）
油料种植面积约为54．88千公顷；（6分）
瓜果蔬菜种植面积约为46．27千公顷；（7分）
其它作物种植面积约为145．9千公顷；（8分）
19.
20.
21. 
22.
23. 200，
24.
25.
26.
27.
28.
29.
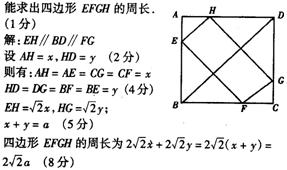
30.
