新课标(北师大版)中考数学第一轮综合练习卷
一、选择题(每小题4分，共40分)
1、下列左边的主视图和俯视图对应右边的哪个物体（ B ）
 |
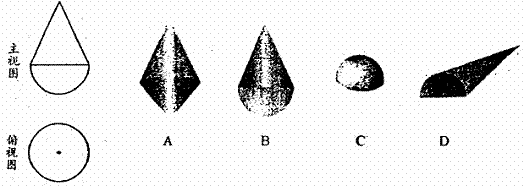2、把a3－ab2分解因式的正确结果是（ C ）
A. (a+ab)(a－ab)
B. a (a2－b2) C. a(a+b)(a－b) D. a(a－b)2
3、不等式组
的解集是（ C ）
A．x＞3 B．x＜2 C．2＜x＜3 D．x＞3 或x＜2
4、抛物线y＝x2＋2x－2的顶点坐标是（ D ）
A.（2，－2） B.（1，－2） C.（1，－3） D.（－1，－3）
5、如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（ B ）
A.30° B.36° C.45° D.70°
6、下列模拟掷硬币的实验不正确的是（ D ）
A．用计算器随机地取数，取奇数相当地正面朝上，取偶数相当于硬币正面朝下
B．在袋中装两个小球，分别标上1和2，随机地摸，摸出1表示硬币正面朝上
C．有没有大小王的扑克中随机地抽一张牌，抽到红色牌表示硬币正面朝上
D．将1、2、3、4、5分别写在5张纸上，并搓成团，每次随机地取一张，取到奇数号表示硬币正面朝上
7、在银行存款准备金不变的情况下，银行的可贷款总量与存款准备金率成反比例关系.当存款准备金率为7.5%时，某银行可贷款总量为400亿元；如果存款准备金率上调到8%时，该银行可贷款总量将减少（ B ） ( ).
A.20亿 B.25亿 C.30亿 D.35亿
8、小明要制作一个圆锥模型，其侧面是由一个半径为9cm，圆心角为240°的扇形纸板制成的，还需要一块圆形纸板做底面，那么这块圆形纸板的直径为（ B ）
A．15cm B．12cm C．10cm D．9cm
9、(针孔成像问题)根据图中(AB∥A/B/)尺寸，那么物像长y(A/B/ 的长)物长x(AB的长)之间函数关系的图象大致是（ C ）
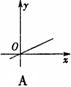
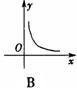
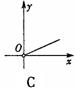
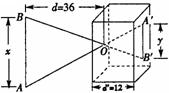
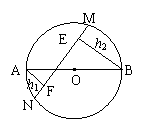10、如图，AB是⊙O的直径，且AB=10，弦MN的长为8，若弦MN的两端在圆周上滑动时，始终与AB相交，记点A、B到MN的距离分别为h1、h2，则│h1-h2│等于（ B ）
A.5 B.6 C.7 D.8
二、填空题(每小题4分，共40分)
11、如图，两条直线a、b被第三条直线c所截，如果a∥b，∠1=70°，那么∠2= 110° .
 |
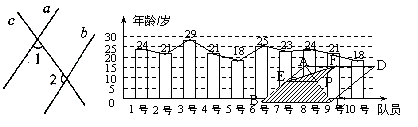(第11题图) (第12题图) (第13题图)
12、如图是2003年~2004赛季青岛足球队1号~10号队员的年龄统计图，根据统计图可知，这10名队员年龄的众数是 21 岁，中位数是 22 岁.
13、如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是__2.5_____.
14、某落地钟钟摆的摆长为0.5米，来回摆动的最大夹角为20º。已知在钟摆的摆动过程中，摆锤离地面的最低高度为a米，最大高度为b米，则b-a=_
(1-cos10°)_____米(不取近似值).
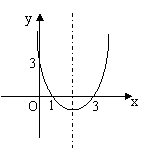
15.抛物线y=ax2+bx+c如右图所示,则它关于y轴对称
的抛物线的解析式是__y=x2+4x+3________.
三、(每小题8分，共16分)
16、计算：
3-
17、下表是某校初三(1)班20名学生某次数学测试的成绩统计表：
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数82分，求x、y的值；
(2)在(1)的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a、b的值.
(1)x=5，y=7；(2)a=90，b=80.
四、(每小题9分，共18分)
18、图1是海口市年生产总值统计图，根据此图完成下列各题：
(1)2003年我市的生产总值达到 亿元，约是建省前的1987年的 倍(倍数由四舍五入法精确到个位)；
(2)小王把图1的折线统计图改为条形统计图，但尚未完成(如图2)，请你帮他完成该条形图；
(3)2003年我市年生产总值与2002年相比，增长率是 %(结果保留三个有效数字)；
(4)已知2003年我市的总人口是139.19万，那么该年我市人均生产总值约是 元(结果保留整数).
(1)238.18, 19 (2)作图(略) (3) 13.0, (4) 17112元
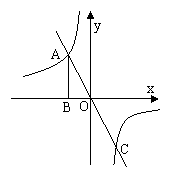19、如图，Rt△ABO的顶点A是双曲线y=
与直线y=kx在第二象限的交点，AB⊥x轴于B且S△ABO=1.
（1）求这两个函数的解析式
（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
(1)y=
y=-2x (2)x<-1或0<x<1
五、(每小题10分，共20分)
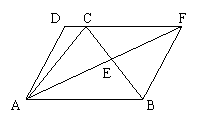
20、如图，梯形ABCD，AB//DC，E是BC的中点，AE、DC的延长线相交于点F，连接AC、BF.
(1)求证：AB=CF；
(2)四边形ABFC是什么四边形？请说明理由.
(1)略 (2)四边形ABFC是平行四边形 理由略
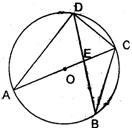
21、如图，AC是⊙O的直径，弦BD交AC于点E．
(1)求证：△ADE∽△BCE；
(2)若CD=OC，求sinB的值．
(1)略 (2)
六、(本题12分)
22、据统计，连云港港口2002年、2003年的内外贸吞吐总量分别为3300万吨和3760万吨，其中2003年外贸和内贸吞吐量分别较2002年增长10%和20%．
（1）试确定2002年的外贸和内贸吞吐量；
（2）2004年港口内外贸吞吐量的目标是：总量不低于4200万吨，其中外贸吞吐量所占比重不低于60%．预计2004年的内贸吞吐量较2003年增长10%，则为完成上述目标，2004年的外贸吞吐量较2003年至少应增加多少万吨？
(1) 2002年内贸、外贸吞吐量分别为1300万吨和2000万吨．（2）2004外贸吞吐量较2003年至少应增加374万吨
七、(本题12分)
23、(1)在2004年6月的日历中(见下左图)，任意圈出一竖列上相邻的三个数，设中间的一个数为a ，则用含a的代数式表示这三个数(从小到大排列)分别是 .
 |
(2)现将连续自然数1至2005按图中的方式排成一个长方形阵列，用一个正方形框出16个数(如上右图)
①图中框出的16个数的和是 ；
②在上右图中，要使一个正方形框出的16个数之和分别等于2000，2005，是否可能？若不可能，试说明理由，若有可能，请求出该正方形框出的16个数中的最小数和最大数.
(1)a-7，a，a+7 (2)①352 ②框出的16个数之和等于2000是可能的，这时方框中最小的数是113，最大数是137；框出的16个数之和不可能等于2005.
八、(本题12分)
24、如图，矩形ABCD中，AB=6，BC=4.
(1)画出以矩形的两条对称轴为坐标轴(x轴平行于AB)平面直角坐标系，并写出点A，BC的中点E，DC的中点F的坐标；
(2)求过点A、E、F三点的抛物线的解析式，并写出此抛物线的顶点坐标.
 |
(1)图略，A(-3，-2)，E(3，0)，F(0，2)
(2)y= -
x2+x+2，顶点(，
)