中考数学模拟考试（2）
班级 学号 姓名 成绩
一、选择题（本题有17小题,每小题3分，共51分）下列各题所附的四个选项中，有且只有一个是正确的,请把正确选项前面的字母填在表内，否则不给分
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 答案 |
1．
的倒数是（ ）
A．2 B．－2 C． D．－
2．化简:
等于（ ）
A．2
B．
C．
D．
3．2003年3月末,我国城乡居民储蓄存款余额达94600亿元，用科学记数法表示为（ ）
A．94.6×102 亿元 B．9.46×103亿元
C．9.46×104亿元 D．0.946×105亿元
4．若点(－1,2)是反比例函数
图象上一点,则k的值是（ ）
A．－ B． C．－2 D．2
5．翰林汇 数轴上所有的点表示的数是 ( )
(A)自然数； (B)实数； (C)无理数； (D)有理数。
6、如果梯形一底边长为6,中位线长为8,那么另一底边长为（ ）
A．4 B．7 C．10 D．14
7.若圆的一条弦把圆分成度数的比为1∶3的两条弧，则劣弧所对的圆周角等于（ ）
（A）45° （B）90° （C）135° （D）270°
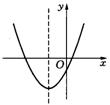8.已知，如图为二次函数
的图象，则一次函数
的图象不经过（ ）
（A）第一象限 （B）第二象限
（C）第三象限 （D）第四象限
9.在下列图形中（每个小四边形皆为全等的正方形），可以是一个正方体表面展开的是（
）
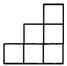
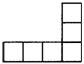
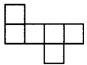
A B C D
10顺次连结等腰梯形各边中点所得的四边形一定是
A．菱形 B．矩形 C．梯形 D．正方形
11．已知⊙O1与⊙O2内切，它们的半径分别为2和3，则这两圆的圆心距d满足（ ）
A、d=5 B、d=1 C、1<d<5 D、d>5
12．下面给出的是一些产品的图案，从几何图形的角度看，这些图案既是中心对称图形又是轴对称图形的是（ ）
A、
B、
C、
D、
13翰林14、一个正多边形的外角和与内角和的度数的比为1:2, 则这个正多边形的边数为( )
(A)6 (B)8 (C)10 (D)12
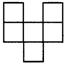
14．如图中的图象（折线ABCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为
千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有（ ）
A、1个 B、2个 C、3个 D、4个
翰林汇15、 已知方程mx2-(1-m)x+m=0有实根，则m满足的条件是 ( )
(A)-1＜m＜
，且m≠0 (B)-1≤m＜，且m≠0
(C)-1≤m≤，且m≠0 (D)m＜-1，m＞
翰林汇16、已知一组数据-2,2,3,-2,x,-1的平均数为0.5,则这组数据的中位数与众数
分别是( ).
(A) 3和-2,-2 (B)0.5,-2 (C)-1和 2,3 (D)0.5,-2和-2
翰林汇17、若函数y1=
,y2=
,则函数y=y1
y2中自变量x的取值范围
为( ).
(A) x
7且x8 (B) x
5且x-7
(C) x5
(D) x5且x-8
二．填空题（ 每空4分，共40分）
1．点（1，2）关于原点的对称点的坐标为 .
2．设x1、x2是方程
的两实数根，则
x1+x2= ， x1·x2= .
3．写出
的一个同类项：
.
4．如图，已知a∥b，∠2=140°，则∠1= °.
5、写出一个以（-2，3）顶点、开口向下的抛物线解析式 .
6、若等腰梯形一底角为
，面积为
，中位线长为
，则此梯形的周长
为 
7、已知圆锥的母线长是5㎝，底面半径是2㎝，则这个圆锥的侧面积是 ㎝2
8、如图，□ABCD中，AE、CF分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是 （只需写出一个即可，图中不能再添加别的“点”和“线”） .
9、根据某市去年7月份中某21天的各天最高气温（℃）记录，制作了如图的统计图，由图中信息可知，记录的这些最高气温的众数是 ℃，其中最高气温达到35℃以上（包括35℃）的天数有 天.
 |
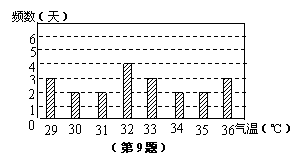10、 在△ABC中，∠C＝90°，若tanA＝
，则sinA＝
；
三、解答题：（每题5分，共20分）
1、计算：
2、分解因式：
3、用换元法解方程：
4、解不等式组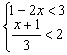
四、解答题：（每题6分，共12分）
1、已知：如图，□ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F.
求证：BE=DF.
 |
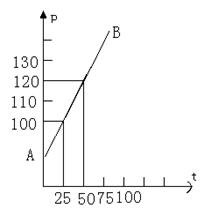
2、、科学家通过实验探究出一定质量的某气体在体积不变的情况下，压强P（千帕）随温度t（
）变化的函数关系式是P=kt+b，其图象是如图所示的射线AB.
（1）根据图象求出上述气体的压强与温度t的函数关系式
（2）求出当压强P为200千帕时，上述气体的温度
五、解答题：（每题6分，共12分）
1、阅读下面的例题：解方程
解：（1）当x≥0时，原方程化为
，解得：
＝2，
＝－1（不合题意，舍去）．
（2）当x＜0时，原方程化为
，解得：＝1（不合题意，舍去），＝－2．
∴ 原方程的根是＝2，＝－2．
请参照例题解方程
，
2、已知：如图，四边形ABCD内接于⊙O，过点A的切线与CD的延长线交于E，且∠ADE=∠BDC.
（1）求证：△ABC为等腰三角形；
（2）若AE =6，BC=12，CD=5，求AD的长.
六、解答题：（第1题7分，第2题8分，共15分）
1、已知，⊙O与直线l相切于点C，直径AB∥l，P是l上C点左边（不包括C点）一动点，AP交⊙O于D，BP交⊙O于E，DE的延长线交l于F．
（1）当PC＜AO时，如图1，线段PF与FC的大小关系是 。结合图1，证明你的结论．
（2）当 PC＞AO时，AP的反向延长线交⊙O于D，其它条件不变，如图2，（1）中所得结论是否仍然成立？
答：
。（不证明）
（3）如图2，当tan∠APB＝，tan∠ABE＝，AP＝
时，求PF的长．
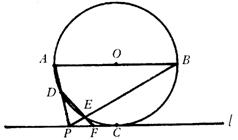
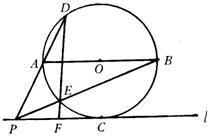
图1 图2
2、
已知，如图，Rt△ABC中，∠B=90°，∠A=30°，
BC=6㎝. 点O从A点出发，沿AB以每秒
㎝的速度
向B点方向运动，当点O运动了t秒（t>0）时，
以O点为圆心的圆与边AC相切于点D，与边AB相交于E、F两点.
过E作EG⊥DE交射线BC于G.
（1）若E与B不重合，问t为何值时，△BEG与△DEG相似？
（2）问：当t在什么范围内时，点G在线段BC上？当t在什么范围内时，点G在线段BC的延长线上？
（3）当点G在线段BC上（不包括端点B、C）时，求四边形CDEG的面积S
（㎝2）关于时间t（秒）的函数关系式，并问点O运动了几秒种时，S取得最大值？最大值为多少？
六题答案：
1、题：
2题：
（1）当t=
或
时，△BEG与△DEG相似.
（2）当
时，点G在线段BC上；当
时，点G在线段BC的延长线上.
（3）当点O运动了秒时，S取得最大值
㎝2.