中考数学模拟试卷4

中考数学模拟试卷4

时间:120分钟　　　满分:120分一、选择题（每小题4分共48分）

1	2	3	4	5	6	7	8	9	10	11	12

　　

　　

　　

1、下列式子结果是负数的是（　　）

（A）－(－3）（B）－　　 （C）　　 （D）

2、2003年10月15日中国“神舟”五号载人飞船成功发射，圆了中国人千年飞天梦想，航天员杨利伟乘飞船在约21小时内环绕地球14圈，每圈长度约42179km，那么飞船环绕地球14圈的长度约为（　　）

（A）5.91×m　 （B）5.91×m　（C）5.91×m　（D）5.91×m

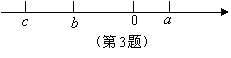3、已知实数、、在数轴上对应的点如图所示，则下列关系式中成立的是（　 ）

（A）＋＞＋　　 （B）＜　　 

（C）－＜－　　 （D）＞　

4、三条边长分别为2、3、8的等腰梯形的周长是（　 ）

（A）15　　　　　　　　 （B）16　　

（C）21　　　　　　　　 （D）15或16或21

5、为测量一河岸相对两建筑物A、B的距离，如图所示，有三位

同学分别测量出了以下三组数据

①AC、∠ACB；

②CD、∠ACB、∠ADB；

③EF、DE、AD.

能根据所测数据，求出A、B间距离的共有（　　 ）

（A）3组　　 （B）2组　　 （C）1 组　　 （D）0组

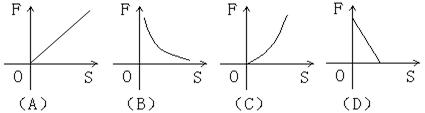
6．已知力F做的功是15焦，则力F与物体在力的方向上通过的距离S的图象大致是图

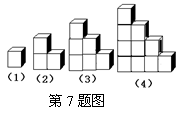
7．如图是由棱长为1的小立方体叠放而成的一组几何体，图（1）中有一个立方体，图（2）中有3个立方体，图（3）中有6个立方体，图（4）中有10个立方体，按此规律叠放下去，则第10个图中的立方体的个数是

A、35　B、45　C、55　D、65

　　　　　　　　　 

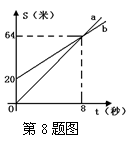
8．小明、小强两人进行百米赛跑，小明比小强跑得快，如果两人同时跑，小明肯定赢，现在小明让小强先跑若干米，图中的射线a、b分别表示两人跑的路程与小明追赶时间的关系，根据图象判断：小明的速度比小强的速度每秒快

 A、1米　B、1.5米  C、2米　D、2.5米

9.下列图形中既是轴对称图形又是中心对称图形的是

A　　　　　　　　　 　B　　　　　　　　　C　　　　　　　　　　　　D

10.某中学新科技馆铺设地面，已有正三角形形状的地砖，现打算购买另一种不同形状的正多边形地砖，与正三角形地砖在同一顶点处作平面镶嵌，则该学校不应该购买的地砖形状是

A、正方形　　　　　　 B、正六边形　　　　 C、正八边形　　　　D、正十二边形

11.设一元二次方程x²+4x—2=0的两个实数根为x₁，x₂，那么的值等于

A、—2　B 、2　 C、—　D、

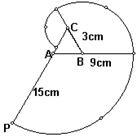
12．如图，有一个边长为6cm的正三角形木块ABC，点P是CA延长线上的一点，在A、P之间拉一条长为15cm细丝，握住点P，拉直细线，把它全部紧紧绕在△ABC木块上（缠绕时木块不动），则点P运动的路线长为（π取3.14，精确到0.1cm）

A、28.3cm　 B、28.2cm　 C、56.5cm　 D、56.6cm　

二、填空题（每小题4分共20分）

13．分解因式：a²－2ab+b²－9=　　　　　　  ；

14．已知a＞0，化简+－a²的

结果是　　　　 ；

15．如图，在圆内接△ABC中，D是BC边的中点，E是AB边的中点，F是AC边是中点，连结DE、DF，要使四边形AEDF为菱形，应补充的一个条件是　　　　　　　  。（只要填上一个你认为恰当的条件即可）

16．小张利用计算机设计了一个计算程序,输入和输出的数据如下表:

输入	…	1	2	3	4	5	…
输出	…						…

　 那么，当输入数据是8时，输出数据是　　　　　　　  .

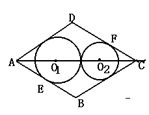
17．如图，已知菱形ABCD，且AB=3，∠B=120°，O₁、O₂是对角线AC上的两个动点，⊙O₁与AB相切于E，⊙O₂与CD相切于F，并且⊙O₁与⊙O₂外切，设⊙O₁的半径为R，设⊙O₂的半径为r，则R+r的值为　　　　  。

三、解答题（共52分）

18．（5分）计算：（－）⁰+（－）^－1+2cos30°－

19.（本小题6分）

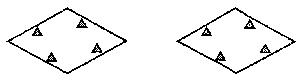
如图，菱形公园内有四个景点，请你用两种不同的方法，按下列要求设计成四个部分：⑴用直线分割；⑵每个部分内各有一个景点；⑶各部分的面积相等。（可用铅笔画，只要求画图正确，不写画法）

20．（6分）解方程：

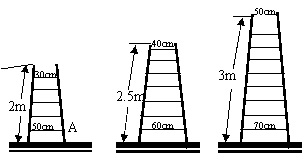21. （8分）有三把梯子，分别是五步梯、七步梯、九步梯，每攀沿一步阶梯上升的高度是一致的。每把梯子的扶杆长（即梯长）、顶档宽、底档宽如图所示，并把横档与扶杆榫合处称作联结点（如点A）。

（1）　　　 通过计算，补充填写下表：

楼梯 种类	两扶杆总长（米）	横档总长（米）	联结点数（个）
五步梯	4	2．0	10
七步梯
九步梯

（2）　　　 一把梯子的成本由材料费和加工费组成，假定加工费以每个个联结点1元计算，而材料费中扶杆的单价与横档的单价不相等（材料损耗及其它因素忽略不计）。现已知一把五步梯、七步梯的成本分别是26元、36元，试求出一把九步梯的成本。

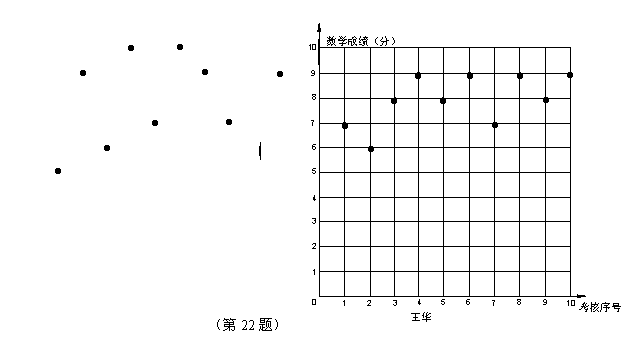
22． （8分）某市初中考核成绩采用“十分制“，刘鹏与王华在上学期的10次数学考核中的成绩（成绩均为整数）分别如下图所示.

(1)利用图中信息,完成下表:

	平均数	中位数	众数	方差
刘鹏	8	8.5	9	2.6
王华

(2)根据图中

信息,应用所学的统计知识,对两人的数学成绩作出评价.

(3)对这两个人分别作出学习建议.

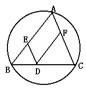
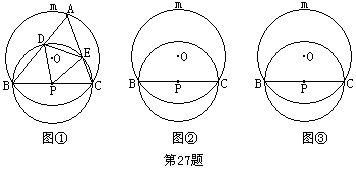
23.（9分）如图，⊙O与⊙P相交于B、C两点，BC是⊙P的直径，且把⊙O分成度数的比为1:2的两条弧，A是上的动点(不与B、C重合)，连结AB、AC分别交⊙P于D、E两点.

　　(1)当△ABC是锐角三角形(图①)时，判断△PDE的形状，并证明你的结论；

　　(2)当△ABC是直角三角形、钝角三角形时，请你分别在图②、图③中画出相应的图形(不要求尺规作图)，并按图①标记字母；

　　(3)在你所画的图形中，(1)的结论是否成立？请就钝角的情况加以证明.

　　

24．（10分）如图：△OAB是边长为的等边三角形，其中O是坐标原点，顶点B在y 轴的正方向上，将△OAB折叠，使点A落在边OB上的A^/点，折痕为EF。

（1）求当A^/E∥x轴时，点A^/和E的坐标；

（2）求当A^/E∥x 轴，且抛物线经过点A^/和E时，该抛物线与x轴的交点的坐标；

（3）当点A^/在OB上运动但不与O、B重合时，△A^/EF能否成为直角三角形？若能，请求出此时点A^/的坐标；若不能，请说明理由。

 

答案

1——12：　 BACCA　BCDDC　BC

13、(a－b＋3)(a－b－3); 14、a;　　15、AB=AC等；　 16、；　 17、；

18、－3；

19、答案不唯一，如

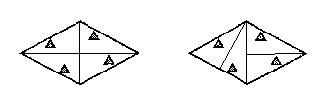
20、x₁=2,　 x₂=;

21、解：（1）七步梯、九步梯的扶杆长分别是5米、6米；横档总长分别是3.5米、3.5米；联结点个数分别是14个、18个。（3分）

　　（2）设扶杆单价为x元/米，横档单价为y元/米。依题意得：即，解得。 故九步梯的成本为6×3+5.4×2+1×18=46.8(元) (9^/).

答:一把九步梯的成本为46.8元。（5分）

22、（1）王华平均数为8,中位数为8,众数为9,方差为1. （3分）

(2)就平均数和众数而言,两人的数学成绩一样好；就中位数而言,刘鹏的成绩比王华的成绩好；就方差而言,王华的10次成绩波动性小,比较稳定. （3分）

(3)略　（2分）

23、(1)△PDE是等边三角形.　　　　　（4分）

　　证明：连DC.∵弦BC把⊙O分成度数的比为1:2的两条弧，∴的度数为120°.

　　　　　　∴∠BAC=60°.∴∠ABC+∠ACB=120°.

　　　　　　又∵PB=PD=PC=PE，∴∠BDP=∠ABC，∠CEP=∠ACB.

　　　　　　∴∠BDP+∠CEP=120°.∴∠BPD+∠CPE=120°.

　　　　　　∴∠DPE=60°.

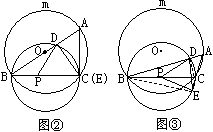　　　　　　又PD=PE，∴△PDE是等边三角形.

　　(2)如图②、图③即为所画图形. （2分）

　　(3)图②和图③中△PDE仍为等边三角形. （3分）

　　　 证明：如图③.连结BE、DC.

　　　　　　 ∵BC为⊙P的直径，∴∠BDC=90°.

　　　　　　 又∵∠A=60°，∴∠ACD=30°.

　　24、（1）当A^/E平行于x轴时∠EA^/O=90°所以∠A^/OE=60°，∠A^/EO=30°，A^/O=EO。设OA^/= a，则OE=2a，AE=A^/E=a，所以a+2 a=2+，a=1，A^/（0，1）、E（，1）（4分）

（2）（交点为：（2，0）和（－，0）（3分）

（3）不能，分三种可能分别简要说明。（3分）