
![]()
![]() 中考数学模拟题(120分钟)
中考数学模拟题(120分钟)
一、选择题:(13×3` = 39`)
1.下列计算中,正确的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
2.在3,2. 3561……,![]() ,(3. 14-π)0四个数中,有理数( )个.
,(3. 14-π)0四个数中,有理数( )个.
A、1 B、2 C、3 D、4
3.下列说法中,正确的是( )
A、2-1与2互为相反数 B、![]() +
+![]() 与
与![]() -
-![]() 互为倒数
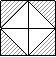
互为倒数
C、关于x的方程x2 = -a无解 D、x2+2x+3 = 0的两根和是-2
4.“世界银行全球扶贫大会”于2005年5月26日在上海开幕.从会上获知,我国国民生产总值达到11.69万亿元,人民生活总体上达到小康水平,其中11.69万亿用科学记数法表示应为( )
A、11.69×![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.已知α、β是两个钝角,计算![]() 的值,甲、乙、丙、丁四位
的值,甲、乙、丙、丁四位
同学算出了四种不同的答案分别为240、480、760、860,其中只有一个答案是正确的,则正确的答案是( )
A、860 B、760 C、480 D、240
6.张师傅下岗再就业,做起了小商品生意,第一次进货时,他以每件a元的价格购进了20件甲种小商品,每件b元的价格购进了30件乙种小
商品(a>b);回来后,根据市场行情,他将这两种小商品都以每件![]()
元的价格批发给李老板,在这次买卖中,张师傅是( )
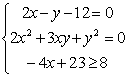 A、不赚不赔 B、赔钱 C、赚钱 D、无法确定赚和赔
A、不赚不赔 B、赔钱 C、赚钱 D、无法确定赚和赔
7、计算:解方程(不等式)组 的结果是( )
A、这是错题,无解
B、有两组解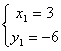 和
和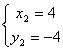
C、有一组解![]() D、有一组解
D、有一组解![]()
8. 一列列车自2004年全国铁路第5次大提速后,速度提高了26千米/时,现在该列车从甲站到乙站所用的时间比原来减少了1小时,已知甲、乙两站的路程是312千米,若设列车提速前的速度是x千米,则根据题意所列方程正确的是( )
A、![]() B、
B、![]()
 C、
C、![]() D、
D、![]()
9.如图2,在菱形ABCD中,∠ABC=60°.
AC=4.则菱形ABCD的内切圆半径为( )
(A)2![]() (B)
(B)![]() (C)
(C)![]() (D)2
(D)2
10.已知一元二次方程x2-3x-6=0有两个实数根x1、x2,则经过点A(x1+x2,x1x2)的反比例解析式为( )
A、y = ![]() B、y =
B、y = ![]() C、y =
C、y =![]() D、y=
D、y=![]()
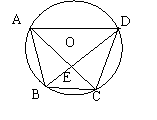 11.
如图,已知四边形ABCD是⊙O的内接四边形,
11.
如图,已知四边形ABCD是⊙O的内接四边形,
且AB=CD=5,AC=7,BE=3,下列命题错误的是( )
A、 图中全等的三角形共有2对 B、∠AEB=90º
C、∠BDA=45º D、△AED∽△BEC
12.有一块缺角矩形地皮ABCDE(如图4),其中AB=110m,BC=80m,CD=90m,∠EDC=135°.现准备用此块地建一座地基为长方形(图中用阴影部分表
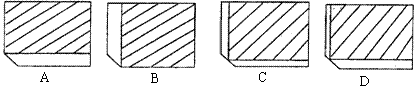
 示)的教学大楼,以下四个方案中,地基面积最大的是( )
示)的教学大楼,以下四个方案中,地基面积最大的是( )
13.如图:向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度![]() 与注水时间
与注水时间![]() 之间的函数关系大致是下列图象中的(
)
之间的函数关系大致是下列图象中的(
)
 |

二、填空题:(7×3` = 21`)
14.已知二次函数y = x2+mx+n与x轴有两个交点A(-2,0)、B(1,0)。分解因式:x2+mx+n= .
15.函数![]() 的自变量x的取值范围是__________.
的自变量x的取值范围是__________.
 16.已知x =
16.已知x =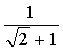 ,则
,则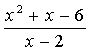 +
+![]() 的值为 。
的值为 。
17.边长为1的三个正方形,组成如图的方格形图,图中共
有8个格点,任取其中三个能组成面积为1的等腰直角三角形 个。
18.做一做:用四块如图1的瓷砖设计正方形拼图方案:使拼成的图案在图2只成轴对称图形,在图3中只成中心对称图形,在图4中既成轴对称图形又成中心对称图形(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示).
 |
19.若⊙O的半径为2㎝,其中一条弦长为2![]() ㎝,则这条弦所对的弧度数
㎝,则这条弦所对的弧度数
是________;
20.观察下列数表:
![]() 1 2 3 4 … 第一行
1 2 3 4 … 第一行
2 3 4 5 … 第二行
3 4 5 6 … 第三行
![]()
![]()
![]()
![]() 4 5 6 7 … 第四行
4 5 6 7 … 第四行
根据数表所反映的规律,第n行第n列交叉点上的数应为
三、解答题:(共90`)
21.(12`)计算:![]()
22.(12`)已知![]() , (1) 求x2 -x 的值(2)求x 的值
, (1) 求x2 -x 的值(2)求x 的值
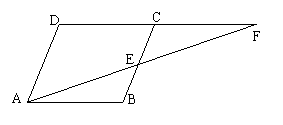
![]() 23.(14`)已知:如图,
23.(14`)已知:如图,![]() ABCD中,E是BC的中点,直线AE交DC的延长线于点F。(1)图中有
对相似三角形,有 对全等三角形。并任选一对进行证明。
ABCD中,E是BC的中点,直线AE交DC的延长线于点F。(1)图中有
对相似三角形,有 对全等三角形。并任选一对进行证明。
(2)若AF =26,BC=10,AB=12,求把△ABE以AB为轴旋转一周所得的立体图的表面积。
 |
24.(14`)江油市教体局为了了解本市中小学实施素质教育的情况,抽查了某校初一年级甲、乙两个班的部分学生,了解他们在一周内(星期一至星期五)参加课外活动的次数情况,抽查结果统计如下图:
(1)在这次抽查中,甲、乙班被抽查了多少人?
(2)在被抽查的学生中,甲、乙班学生参加课外活动的平均次数分别是多少次?根据以上信息,用你学过的知识,估计甲、乙两班在开展课外活动方面哪个班级更好一些?
(3)在被抽查的学生中,甲、乙两班学生参加课外活动的平均次数又是多少?已知全江油市有中小学生10000人,江油市教体局想把每周参加5次课外活动的爱动手动脑的学生组织起来搞一个主题活动,你估计有多少这样的学生?江油市教体局向全体学生进行问卷调查发现:每周参加5次课外活动的学生有273人,你的估计与这个数据一致吗?如果不一致,问题在哪里?
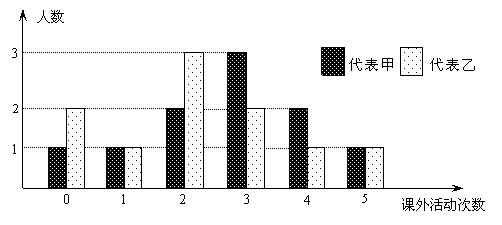 |
25.(10`)如图,已知测速站F到公路L的距离FO为40米,一辆汽车在公路L上行驶,测得此车从点A行驶到点B所用的时间为2秒,并测得∠AFO=600,
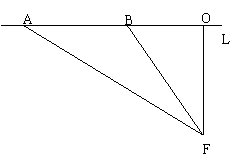 ∠BFO=300,计算此车从A到B的平均速度为每秒多少米(结果保留四个有效数字),并判断此车是否超过了每秒22米的限制速度。(资料:
∠BFO=300,计算此车从A到B的平均速度为每秒多少米(结果保留四个有效数字),并判断此车是否超过了每秒22米的限制速度。(资料:![]() =1.414,
=1.414,![]() =1.732,
=1.732,![]() =2.236,
=2.236,![]() =2.449, ……)
=2.449, ……)
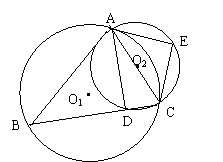 26.(14`)已知:如图,△ABC内接于⊙O1,以AC为直径的⊙O2交BC于点D,AE切⊙O1于点A,交⊙O2于点E.连AD、CE,若AC=7,AD=3
26.(14`)已知:如图,△ABC内接于⊙O1,以AC为直径的⊙O2交BC于点D,AE切⊙O1于点A,交⊙O2于点E.连AD、CE,若AC=7,AD=3![]() ,
,
tanB=![]()
![]() .求BC的长.
.求BC的长.
![]() 27.(14`)在举世关注牲畜口蹄疫战争中,某医药厂接受了生产一批高质
27.(14`)在举世关注牲畜口蹄疫战争中,某医药厂接受了生产一批高质
量医用疫苗针剂的任务。要求在8天之内(含8天)生产A型和B型两种
型号的疫苗针剂共5万只,其中A型疫苗针剂不得少于1.8万只,该厂的
生产能力是:生产A型疫苗针剂的生产线每天能生产0.6万只,生产B型
疫苗针剂的生产线每天能生产0.8万只,已知生产一只A型疫苗针剂可获
利0. 5元,生产一只B型疫苗针剂可获利0. 3元。问:(1)设该厂在这次
任务中生产了A型疫苗针剂x万只。该厂生产A型疫苗针剂可获利润____
万元,生产B型疫苗针剂可获利润____万元,全部生产A型疫苗针剂需要
天,全部生产B型疫苗针剂需要 天。
设该厂这次生产疫苗针剂的总利润是y万元,试写出y关于x的函数关系
式,并写出自变量x的取值范围
(2)如果你是该厂厂长:①在完成任务的前提下,你如何安排生产A型和
B型疫苗针剂的只数,使获得的总利润最大?最大利润是多少?
②若要在最短时间内完成任务, 最短时间是多少?你又如何来安排生产A型
和B型疫苗针剂的只数?
数学模拟题供参考答案
一.ABBCA CDCBD ABB
二.14.(x+2)(x-1) 15.X≤5且x≠2
16.4 17、6

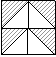 18.图2:
或其它;图2:
或其它;图2:
或其它;
18.图2:
或其它;图2:
或其它;图2:
或其它;
19.90°和270° 20、2n-1
三.21、解:原式 = -![]() ×2×4-
×2×4-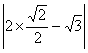 -
-![]() +
+![]() …………6`
…………6`
=-2-(![]() )-2
)-2![]() +2
+2![]() +2 ……………………4`
+2 ……………………4`
=![]() ………………………………………………………2`
………………………………………………………2`
22.解:(1)![]()
去分母得:(x2-x)2+3(x2-x)-4=0…………………………………2`
(x2-x+3)(x2-x-1)=0…………………………………2`
∵x2-x+3=(x-![]() )2+
)2+![]() >0…………………1`
>0…………………1`
∴x2-x-1=0
∴x2-x =1……………………………………………………3`
(2)由(1)x2-x-1=0 解得x =![]() =
=![]() …………4`
…………4`
23.(1)填空:3;1………………………………………2`
求证:略……………………………………1`
证明:略……………………………………3`
(2)在![]() ABCD中,AB∥DF,则
ABCD中,AB∥DF,则![]() =
=![]()
∵E是BC的中点,即![]() = 1
= 1
∴BE =![]() BC =
BC =![]() ×10 = 5, AE =
×10 = 5, AE =![]() AF =
AF =![]() ×26 =13……………………2`
×26 =13……………………2`
∴AE2 =132 =169,AB2+BE2 =122+52 =169
∴△ABE是以AE为斜边的直角三角形………………………………2`
∴把△ABE以AB为轴旋转一周所得的立体图是底面半径r =5,高h =12,母线长为13的圆锥。………………………………………………………1`
圆锥表面积S =52π+![]() ×13×2π·5 =90π…………………………3`
×13×2π·5 =90π…………………………3`
24.解(1)甲班抽查的人数为:1+1+2+3+2+1 =10(人)……2`
乙班抽查的人数为:2+1+3+2+1+1 =10(人)………………2`
(2)![]() =
=![]() (1×0+1×1+2×2+3×3+2×4+1×5)= 2.7 (次/人)……2`
(1×0+1×1+2×2+3×3+2×4+1×5)= 2.7 (次/人)……2`
![]() =
=![]() (2×0+1×1+3×2+2×3+1×4+1×5)= 2.2 (次/人)……2`
(2×0+1×1+3×2+2×3+1×4+1×5)= 2.2 (次/人)……2`
∴甲班在开展课外活动方面比乙班好些.…………………………………2`
(3) ![]() =
=![]() (27+22) = 2.45 (次/人)…………………………2`
(27+22) = 2.45 (次/人)…………………………2`
10000人学生中每周参加5次课外活动的学生估计有10000×![]() =1000(人)
=1000(人)
∵10000人>273人,估计与实际情况相差很多,原因是样本中的班级和人数都太少,不能反映总体情况。……2`
(本题可有其它解法,理由充分有说服力可酌情给分)
25.解:在Rt△BOF中,∠BFO=300,FO = 40,
则BO =![]() OF =
OF = ![]() (米)…………………2`
(米)…………………2`
在Rt△AOF中,∠AFO=600,FO = 40,则AO =![]() OF =
OF = ![]() (米)……2`
(米)……2`
∴AB =AO-BO =![]() -
-![]() =
= ![]() (米)……………………2`
(米)……………………2`
∴此车从A到B的平均速度为![]() ÷2 =
÷2 =![]() ……………………2`
……………………2`
≈23.09(米/秒)…………1`
∵平均速度23.09米/秒>22米/秒,则超过了限时速度。……………1`
26. 8
27. 略。