数学中考模拟考
数 学 试 卷
班级________ _ 姓名_____ ____学号__________成绩____________
| 题号 | 一 | 二 | 三 | 四 | 五 | 总分 |
| 得分 |
一、填空题：(本题共14小题，每小题3分，满分42分）
1、
________；
2、
____________；
3、不等式
的解是______________；
4、在实数范围内因式分解：
_____________________；
5、若
，则 x =
6、函数
的自变量x的取值范围是____________________；
7、抛物线
的顶点坐标为（ ， ）；
8、如图，已知BC=CD=DE=EA,∠A=20°,那么∠B的度数是 度；
9、三角形三边中点连线组成的三角形周长为12，则原三角形周长为__________；
10、已知α为一锐角，且cosα = sin60º，则α = 度；
11、在⊙O中，弦AB= 8cm，弦心距OC= 3cm，则该圆的半径为________cm；
12、一元二次方程
有一个根为1，那么a+b+c的值为 ；
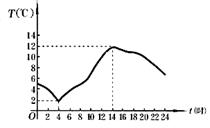
13、 右图是上海某日的气温随时间变化的图象，根据
图象可知，在这一天中最高气温是 度
达到最高气温的时刻分别是__________________.；
14、如下图，由小正方形组成的L形图中，请你用三种方法分别在下图中添画一个小正方形使它成为轴对称图形：
方法一 方法二 方法三
二、单项选择题：【每题列出的四个答案中，只有一个是正确的，把正确答案的代号填入括号内】（本题共4小题，每小题3分，满分12分）
15、已知方程
，如果设
，那么原方程可变形为
（ ）
A、
B、
C、
D、
16、在Rt△ABC中，∠C＝90º，c=5，a=4，则sinA的值为 ( )
A、
B、
C、
D、
17、函数y=(2m－1)x是正比例函数，且y随自变量x的增大而增大，则m的取值范围是 ( )
A、m<
B、m>
C、m≥
D、m≤
18、三角形的外心恰好在它的一条边上，则这个三角形一定是 ( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、斜三角形
三、简答题：（本题共3小题，每小题8分，满分24分）
19、计算： 
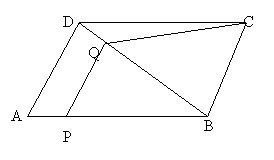
20、如图，已知四边形ABCD中，P为对角线AC上一点，若AD＝AB，PD＝PB，求证：AC平分∠BCD。
D
A P C
B
21、部分学生参加了一项科技竞赛，已知竞赛成绩分数都是整数，试题满分为140分，参赛学生的成绩分数分布情况如下：
| 分数段 | 0－19 | 20－39 | 40－59 | 60－79 | 80－99 | 100－119 | 120－140 |
| 人 数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
请根据以上信息解答下列问题：
(1) 共有多少人参加本次科技竞赛？最低分和最高分在什么分数范围？
(2) 经竞赛组委会评定，竞赛成绩在60分以上 (含60分)的考生均可获得不同等级的奖励，求参加本次竞赛考生的获奖比例；
(3) 竞赛成绩分数的中位数落在哪个分数段内？
| |
| |
四、解答题：（本题共3小题，每小题10分，满分30分）
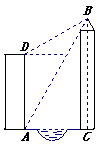
22、如图，在△ABC中，已知∠ABC＝90°，AB上一点E，以BE为直径的⊙O恰与AC相切于D，若AE＝2cm，AD＝4cm。
求：(1)⊙O的直径BE的长；
(2)
△ABC的面积。
 |
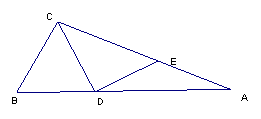
23、如图，小丽的家住在锦江河畔的电梯公寓AD内，她家的河对岸新建了一座大厦BC。为了测得大厦的高度，小丽在她家的楼底A处测得大厦顶部B的仰角为60º，爬上楼顶D处测得大厦的顶部B的仰角为30º。已知小丽所住的电梯公寓高82米，请你帮助小丽计算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。（计算结果保留根号）
24、已知：如图，开口向下的抛物线 
与x轴交于A、B两点（点A在点B的左侧），抛物线上另有一点C在第一象限，且使△OCA∽△OBC。
（1）求点A和点B的坐标；
（2）求线段OC的长及 
的值；
（3）设直线BC与y轴交于点P，当C是BP的中点时，求直线BP的解析式和抛物线的解析式。
y
P
C
O A B x
五、综合题（本题共3小题，第1小题3分，第2小题6分，第3小题3分，满分12分）
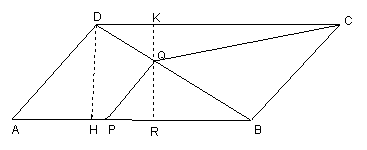
25、在平行四边形ABCD中，AB=5，AD=3，sinA=
，点P是AB上一动点，（点P不与点A、点B重合），过点P作PQ∥AD交BD于Q，连结CQ，设AP
的长为x，四边形QPBC的面积为y。
（1）计算平行四边形ABCD的面积；
（2）写出y关于x的函数解析式，并指出自变量x的取值范围；
（3）是否存在实数x，使得
？如果存在，求出x的值；如果不存在，请说明理由。
 |
中考模拟考数学试卷
参考答案及评分说明
一、 填空题：（本题共14小题，每小题3分，满分42分）
⑴ 4； ⑵ x12； ⑶ x＞
； ⑷ (x＋1)(x＋2)； ⑸ x＝1或x＝0；
⑹ ⑺ （1，3） ⑻ 60； ⑼ 24； ⑽ 30； ⑾ 5；
⑿ 0； ⒀ 12，14时（或下午2时）（错一格不给分） ⒁ 略。（每个方法1分）
二、 单项选择题：（本题共4小题，每小题3分，满分12分）
⒂ B； ⒃ B； ⒄ B； ⒅ B
三、
简答题：（本题共3小题，每小题8分，满分24分）
⒆ 解：原式＝ （每项1分，共4分）
 |
 |
（每项1分，共2分）
⒇ 证明： 在△ADP和△ABP中
AD＝AB （已知）
∵ AP＝AP （公共边）
DP＝PB （已知）
∴ △ADP≌△ABP （S，S，S） （3分）
∴ ∠DAP＝∠BAP （1分）
在△ADC和△ABC中
∵ AD＝AB （已知）
∠DAC＝∠BAC （已证）
AC＝AC （公共边）
∴ △ADC≌△ABC （S，A，S） （3分）
∴ ∠ACD＝∠ACB
∴ AC平分∠BCD （1分）
(21) 答：⑴共有300名学生参加了本次科技竞赛，最低分在20—39分之间，最高分
在120—140分之间。 （3分）
⑵本次竞赛共 195人获奖，获奖率为65％ （2分）
⑶竞赛成绩分数的中位数落在60—79分分数段内 （1分）
⑷如“120分以上有12人；60分至79分分数段的人数最多；……”等 （2分）
四、解答题：（本题共3小题，每小题10分，满分30分）
(22) 解：⑴ 连接OD， ∵ AC切⊙O于D
∴ OD⊥AC （1分）
设⊙O的半径为r，在Rt△AOD中
(r＋2)2＝42＋r2 （1分）
解得 r＝3 （1分）
∴⊙O的直径BE的长为6cm （1分）
⑵ 在Rt△ADO和Rt△ABC中 AB＝AE＋EB＝8cm （1分）
∵ ∠A＝∠A （公共角）
∴ Rt△ADO∽△Rt △ABC (1分)
∴ （1分）
∴
（1分）
∴ （2分）
（数值1分，单位1分）
(23) 过D作DE⊥BC垂足为E （1分）
解：设BE＝x米
在Rt△BDE中，∠BDE＝30°，BE＝x
∴ DE＝
（2分）
在Rt△ABC中，∠BAC＝60°，BC＝82＋x
∴
（2分）
∵ DE＝AC ∴ （1分）
∴ x＝41 （1分）
∴ BC＝82＋41＝123（米） （1分）
AC＝ （米） （1分）
答：大厦高度BC为123米，大厦和电梯公寓的距离AC＝ 米 （1分）
(24) 解⑴令 ax2－8ax＋12a＝0 （1分）
x2－8x＋12＝0 解得 x1＝2，x2＝6
∴ A(2，0)，B(6，0) （1分）
⑵ ∵ △OCA∽△OBC
∴
∴ OC2＝OB·OA＝12 ∴
（1分）
又
（1分）
⑶ ∵
C是BP的中点 ∴在Rt△OPB中 OC＝BC＝PC＝
∴ C点的横坐标 x＝3，由OC＝
得y= ∴C（3， ） （2分）
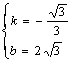
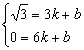∵ C点在直线BP上，BP的直线方程为y＝kx＋b
∴
∴
（2分）
∵ C点在抛物线上， ∴
∴
抛物线解析式为 （2分）
四、
综合题：（本题共3小题，第1小题3分，第2小题6分，第3小题3分，满分12分）
（25）⑴ 作DH⊥AB垂足为H （1分）
∵ 在Rt△ADH中
∴ DH ＝AD·sinA＝2 （1分）
∴ S ABCD＝AB·DH＝5·2＝10 （1分）
⑵ ∵ PQ∥AD ∴
∴
（1分）
过Q作直线KR∥DH交AB于R，交CD于K，在平行四边形ABCD
∵ DH⊥AB ∴ KR⊥AB，KR⊥CD
∵ ∠QPB＝∠A ∴ sin∠QPB＝
∴
（1分）
∴
（1分）
（1分）
（1分）
∴
∴
（0＜x＜5）
（1分）
 |
⑶ 当 （1分）
解得 x1＝0或x2＝5 （1分）
∵ 0＜x＜5
∴ 不存在实数x，使S△BPQ＝S△BCQ （1分）