同步——圆（一）

同步——圆（一）

---------圆的有关性质

复习阅读精要

1、  概念：圆；同心圆；等圆；弦、直径；弦心距；弧、半圆、优弧、劣弧；弓形（及弓形高）；等弧；三角形的外接圆和外心；圆内接多边形；圆心角；圆周角。

2、  点、圆位置关系判定公式：设圆的半径为R，点和圆的距离为d，则

d>Ró点在圆外；　　　　　　　 d=Ró点在圆上；　　　　　　　 d<Ró点在圆内。

3、  相关定理与性质：垂径定理（P₇₆）及推论（_­P₇₈）；圆心角、弧、弦、弦心距之间的关系定理及推论（P₈₇）；圆周角与圆心角关系定理（P₉₁）与推论（P_93-94）；圆内接三角形与四边形的性质（P₉₇）。

练习

一、填空：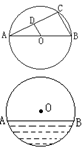

1、  已知圆内一弦AB的长为24，弦AB的弦心距为5，则这个圆的半径等于_________。

2、  如图，已知AB为⊙O的直径，AC为弦，OD∥BC，BC=6cm，则OD=_________。

3、  一个水平放着的圆柱形水管的截面如图所示，如果水管直径40cm，水面的高为10cm，那么水面宽AB=_______。

二、选择：

1、在⊙O中，弦AB的为8cm，AB弦的弦心距的长为3cm，则⊙O的半径长为（　 ）

A、 cm　 B、5 cm　 C、7 cm　 D、cm

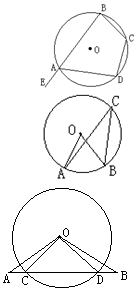
2、已知，如图，∠EAD是圆内接四边形ABCD的一个外角度，则（　 ）

A、∠AED=∠B 　 B、∠EAD=∠D

C、∠EAD=∠C　　D、∠EAD=∠B+∠C

3、如图，圆心角∠AOB=60°，则圆周角∠ACB的度数是（　 ）

A、120°　B、60°　C、30°　D、20°

三、解答题：

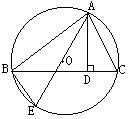
1、  已知：如图，在⊙O中，CD为弦，A、B两点在CD的两端延长线上，且AC=BD。求证：△OAB为等腰三角形。

证明：

2、如图，AD是△ABC的高，AE是△ABC的外接圆直径。求证：△ABE∽△ADC。

证明：

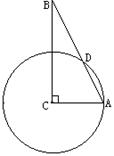3\已知，如图，在△ABC中，∠ACB=90°，∠B=25°，以C为圆心，CA为半径的圆交AB于D。求：弧AD的度数。

解：