新课标(北师大版)中考数学第一轮复习测试卷
第七单元 统计
一、选择题(每小题4分，共40分)
1、下列调查，比较容易用普查方式的是（ B ）
A.了解合肥市居民年人均收入 B.了解合肥市初中生体育中考的成绩
C.了解合肥市中小学生的近视率 D.了解某一天离开合肥市的人口流量
2、若数据2，x，4，8的平均数是4，则这组数据的中位数和众数是（ A ）
A. 3和2 B. 2和3 C. 2和2 D. 2和4
3、9位学生的鞋号由小到大是：20，21，21，22，22，22，22，23，23．这组数据的平均数、中位数和众数中，鞋厂最感兴趣的是（ C ）
A.平均数 B.中位数 C.众数 D.平均数和中位数
4、下表是两个商场 1至 6 月份销售“椰树牌天然椰子汁”的情况（单位：箱）
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | |
| 甲商场 | 450 | 440 | 480 | 420 | 576 | 550 |
| 乙商场 | 480 | 440 | 470 | 490 | 520 | 516 |
根据以上信息可知（ D ）
A.甲比乙的月平均销售量大 B.甲比乙的月平均销售量小
C.甲比乙的销售量稳定 D.乙比甲的销售量稳定
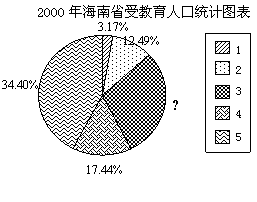5、第五次全国人口普查资料显示，2000年海南省总人口为786.75万，图中表示该省2000年接受初中教育这一类别的数据丢失了，那么结合图中信息，可推知2000年海南省接受初中教育的人数为（ B ）
A.24.94万 B.255.69万
C.270.64万 D.137.21万
6、要了解全市九年级学生身高在某一范围内的学生所占比的大小需知道相应样本的( D )
A.平均数 B.方差
C.众数 D.频数分布
7、对某班60名同学的一次数学测验成绩进行统计，如果频数分布直方图中80.5～90.5分这一组的频数是18，那么这个班的学生这次数学测验成绩在80.5～90.5分之间的频率是( C )
A. 18 B．0.4 C. 0.3 D．0.35
8、人数相等的甲、乙两班学生参加了同一次数学测验, 班级平均分和方差如下：平均分都为110，甲、乙两班方差分别为340、280，则成绩较为稳定的班级为( B )
A．甲班 B．乙班 C. 两班成绩一样稳定 D．无法确定
9、一组数据13，14，15，16，17的标准差是( A )
A.
B.10 C.0 D.2
10、如果将所给定的数据组中的每个数都减去一个非零常数, 那么该数组的( A )
A．平均数改变, 方差不变 B．平均数改变，方差改变
C．平均数不变，方差改变 D．平均数不变，方差不变
二、填空题(每小题4分，共40分)
11、下表是食品营养成分表的一部分(每100克食品中克食部分营养成分的含量).
| 蔬菜种类 | 绿豆芽 | 白菜 | 油菜 | 卷心菜 | 菠菜 | 韭菜 | 胡萝卜 (红) |
| 碳水化合物(克) | 4 | 3 | 4 | 4 | 2 | 4 | 7 |
在表中提供的碳水化合物的克数所组成的数据中，中位数是 4 ，平均数是 4 .
12、在一块试验田里抽取1 000个小麦穗，考察它的长度(单位：厘米)，从频数分布表中看到数据落在5.75～6.05之间的频数为360，于是可以估计这块试验田里长度在5.75～6.05厘米之间的麦穗约占 36% .
一组数据4，0，1，-2，2的标准差是 .
13、某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别做上标记，然后放还．待有标记的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，发现其中两只有标记．从而估计这个地区有黄羊 400 只．
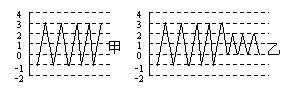
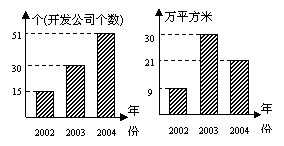14、不通过计算，比较下图中甲、乙两组数据的标准差的大小：s甲 > s乙.
 |
(第14题图) (第15题图)
15、某市对旧城区规划改建，根据2001年至2003年发展情况调查，制作了房地产开发公司个数的条形图和各年度每个房地产开发公司平均建筑面积情况的条形图。利用统计图提供的信息计算这3年中该市平均每年的建筑面积是 702 万平方米.
三、(每小题8分，共16分)
16、某瓜农采用大棚栽培技术种植了一亩地的良种西瓜，这亩地产西瓜约800个，在西瓜上市前该瓜农随机摘下了10个成熟的西瓜，称重如下：
| 西瓜质量（单位：千克） | 5.5 | 5.4 | 5.0 | 4.9 | 4.6 | 4.3 |
| 西瓜数量（单位：个） | 1 | 2 | 3 | 2 | 1 | 1 |
(1)在这个问题中，总体、个体、样本各指什么？
(2)在这个样本中，其众数、中位数、平均数各是什么？
(3)试估计这亩地的西瓜产量约是多少千克。
(1)总体是800个西瓜的质量，个体是每个西瓜的质量，样本是所抽取的10个西瓜的质量. （2）5.0，5.0，5 （3）4000 .
17、某公司员工的月工资如下：
| 员工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E |
| 月工资(元) | 6000 | 3500 | 1500 | 1500 | 1500 | 1100 | 1000 |
(1)该公司员工月工资的中位数是 ，众数是 .
(2)该公司员工月工资的平均数是多少？
(3)用平均数还是用中位数和众数描述该公司员工月工资的一般水平比较恰当？
(1)中位数1500，众数1500 (2)该公司员工月工资的平均数为2300(元) (3)用中位数和众数比较恰当.
四、(每小题9分，共18分)
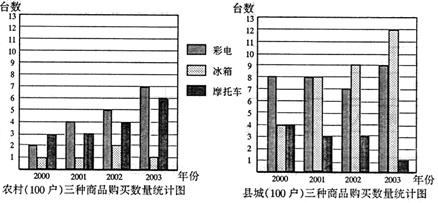
18、下面是统计部门对某地农村、县城近四年彩电、冰箱、摩托车三种商品购买情况的抽样
|
（1）分别对农村、县城三种商品购买的趋势作出大致判断（填“上升”、“下降”、“基本
平衡”）.（3分）
农村购买趋势：彩电 ，冰箱 ，摩托车 .
县城购买趋势：彩电 ，冰箱 ，摩托车 .
（2）若2003年农村购买的彩电平均价格每台1500元，冰箱每台2000元，摩托车每台
4000元；县城购买的彩电平均价格每台2500元，冰箱每台3000元，摩托车每台
6000元. 求出农村、县城2003年三种商品消费总值的比.（3分）
19、某区从参加数学质量检测的8000名学生中，随机抽取了部分学生的成绩作为样本，为了节省时间,先将样本分成甲、乙两组,分别进行分析，得到表一;随后汇总整个样本数据，得到部分结果,如表二.
表一 表二
 |
请根据表一、表二所示信息回答下列问题:
(1) 样本中,学生数学成绩平均分为 分(结果精确到0.1);
(2) 样本中,数学成绩在[84，96）分数段的频数为 ,等第为A的人数占抽样学生总人数的百分比为 ,中位数所在的分数段为 ;
(3) 估计这 8000名学生数学成绩的平均分约为 分(结果精确到0.1).
(1)92.2 (2)72,35% (3)[84,96) (4)92.2
五、(每小题10分，共20分)
20、某教育部门为了研究城市独生子女人格发展状况，随机抽取了某地区300名中学和学生和300名中学生家长进行调查.下面是收集有关数据汇总后绘制的两个统计图：
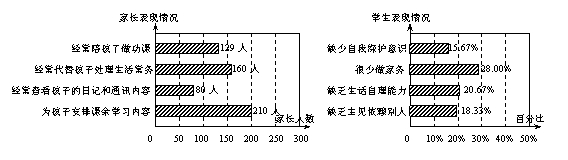
观察上面的统计图，回答下面问题：
(1)在被调查的300名学生中，有多少人“缺乏生话自理能力”？(结果取整数)
“经常陪孩子做功课”的家长占被调查的300名家长的百分比是多少？
(2)若该地区独生子女家长有10万人，请估计有多少家长“为孩子安排课余学习内容”？
(3)从上面的两个统计图中，你还能发现哪些信息，根据你发现的信息提出一个问题.(不解答)
21、某学校对初中毕业班经过比较后，决定从初三(1)(4)(8)班这三个班中推荐一个班为市级先进班集体的侯选班。现对这三个班进行综合素质考评，下表是它们五项素质考评的得分表(以分为单位，每项满分为10分)：
| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 初三(1)班 | 10 | 10 | 6 | 10 | 7 |
| 初三(4)班 | 10 | 8 | 8 | 9 | 8 |
| 初三(8)班 | 9 | 10 | 9 | 6 | 9 |
(1)请问各班五项考评分的平均数、中位数和众数中哪个统计量不能反映三个班的考评结果的差异？并从中选择一个能反映差异的统计量将他们得分进行排序；
(2)根据你对表中五个项目的重要程度的认识，设定一个各项考评内容的占分比例(比例的各项须满足：均为整数；总和为10；不全相同)，按这个比例对各项的得分重新计算，比较出大小关系，并从中推荐一个得分最高的班级作为是级先进班集体的侯选班.
(1)初三(1)班考评分的平均数为8.6分，中位数为10分，众数为10分；初三(4)班考评分的平均数为8.6分，中位数为8分，众数为8分；初三(8)班考评分的平均数为8.6分，中位数为9分，众数为9分；平均数不能反映这3个班的考评结果的差异，而用中位数(或众数)能反映差异.（2）略.
六、(本题12分)
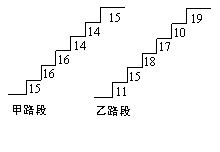
22、在某旅游景区上山的一条小路上，有一些断断续续的台
阶.如图是其中的甲、乙段台阶路的示意图.
请你用所学过的有关统计知识（平均数、中位数、方差
和极差）回答下列问题：
（1）两段台阶路有哪些相同点和不同点？
（2）哪段台阶路走起来更舒服？为什么？
（3）为方便游客行走，需要重新整修上山的小路.对于
这两段台阶路，在台阶数不娈的情况下，请你提出
合理的整修建议.
（1）
∴相同点：两段台阶路高度的平均数相同.
不同点：两段台阶路高度的中位数、方差和极差均不相同.
（2）甲路段走起来更舒服一些，因为它的台阶高度的方差小.
（3）每个台阶高度均为15cm（原平均数），使得方差为0.
七、(本题12分)
23、为了从甲、乙两名学生中选拔一人参加今年六月份的全县中学生数学竞赛，每个月对他们的学习水平进行一次测验，图（4）是两人赛前5次测验成绩的折线统计图.
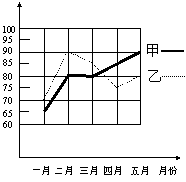(1)别求出甲、乙两名学生 5次测验成绩的平均数及方差.
(2)如果你是他们的辅导教师，应选派哪一名学生参加这次数学竞赛.请结合所学统计知识说明理由.
(1)
甲=80,
乙=80,S2甲=70,
S2乙=50；(2)甲最近2次的成绩不低于乙；甲最近3次的成绩直线上升，而乙的成绩有所下降，所以应选甲参加数学竞赛.
八、(本题12分)
24、某校八年级(5)班分甲、乙两组各选10名学生进行英语抢答，共有10道选择题，答对8道题(含8道题)以上为优秀，各组选手答对题数统计如下：
| 答对题数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数 | 众数 | 中位数 | 方差 | 优秀率 |
| 甲组选手 | 1 | 0 | 1 | 5 | 2 | 1 | 8 | 8 | 8 | 1.6 | 80% |
| 乙组选手 | 0 | 0 | 4 | 3 | 2 | 1 |
请你完成上表，再根据所学的统计知识，从不同方面评价甲、乙两组选手的成绩。
乙的平均数为8，众数为7，中位数为8，方差为1 ，优秀率为60％
故可从以下四个方面作出评价：
(1)从平均数、中位数看都是8道题，成绩均等；
(2)从众数上看，甲组8道题，乙组7道题，所以甲组成绩较好；
(3)从方差上看，甲组成绩差距大，乙组相对稳定、差距不大；
(4)从优秀率看，甲组优秀生比乙组多。