相似形

新课标(北师大版)中考数学第一轮复习测试卷

第十三单元　相似形

一、选择题(每小题4分，共40分)

1、已知，则的值为（　C　 ）

A.　　 B.　　 C.　　 D.

2、在比例尺是1∶8000的南京市城区地图上，太平南路的长度约为25 cm，它的实际长度约为（　 D 　）

A. 320 cm　　　　 B. 320 m　　　　　  C. 2000 cm　　　　D. 2000 m

3、如图，∠1＝∠2＝∠3，则图中相似三角形共有（　D　 ）

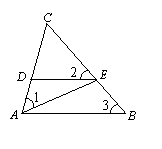A.1对　 　 　B.2对　　 　C.3对　　　　D.4对

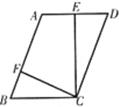
(第3题图)　　　　　　　　  (第4题图)　　　　　　　　  (第5题图)

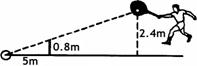
4、小明在打网球时，为使球恰好能过网（网高为0.8m），且落在对方区域离网5m的位置上，已知他击球的高度是2.4m，则她应站在离网的（　 B　 ）

A.15m处　　　B.10m处　　　 C.8m处　 　　 D.7.5m处

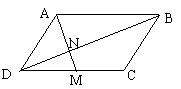
5、如图，在□ABCD中，如果M为CD中点，AM与BD相交于点 N，那么S_△DMN∶S_□ABCD为 （　A　 ）

A、1∶12　　　 　　　B、1∶9　　　　C、1∶8　　 　　　D、1∶6

6、如图是一束平行的阳光从感教室窗户射入的平面示意图，光线与地面所成角AMC=30°，在教室地面的影长MN=2米。若窗户的下檐到教室地面的距离BC=1米，则窗户的上檐到教室地面的距离AC为（　B　 ）

A.2米　　 B.3米　　 C.3.2米　　 D.米

(第6题图)　　　　　　　　 (第7题图)　　　　　　　  (第8题图)

7、如图，在□ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使△CBF∽△CDE，则BF的长是（ D　　）

A.5　　 B.8.2　　 C.6.4　　 D.1.8

8、如图，已知等腰中，顶角∠A=36°，BD为∠ABC的平分线，则的值等于（　B　）

A.　　  B.　　  C. 1 　　　　　D.

9、用作位似图形的方法，可以将一个图形放大或缩小，位似中心位置可选在（  D  ）

A、原图形的外部　　　　　　　 B、原图形的内部

C、原图形的边上　　　　　　　 D、任意位置

10、以下各图放置的小正方形的边长都相同，分别以小正方形的顶点为顶点画三角形，则与△ABC相似的三角形图形为（　 A　 ）

　　　　　　　　　　　　　　　  A　　　　 B　　　　　 C　　　　 D

二、填空题(每小题4分，共20分)

11、科学家研究表明，当人的下肢长与身高之比为黄金比时，看起来最美，某成年女士身高为153cm，下肢长为92cm，该女士穿的高跟鞋鞋跟的最佳高度约为_____2.6_______cm。（精确到0.1cm）

12、如图，D、E分别是△ABC的边AB、AC上的点(DE与BC不平行)，

请你添加一个条件，使△ABC与△AED相似。你添加的条件是　　　　 .

∠ADE=∠C或∠AED=∠B或AD·AB=AE·AC

13、在△ABC中，点D、E分别在边AB、AC上，DE∥BC，AD=1，

BD=2，则S_△ADE∶S_△ABC=　　1∶9　　　 .

14、张明同学想利用树影测量校园内的树高.他在某一时刻测得小树高为1.5米时，其影长为1.2米，当他测量教学楼旁的一棵大树影长时，因大树靠近教学楼，有一部分影子在墙上.经测量，地面部分影长为6.4米，墙上影长为1.4米，那么这棵大树高约___9.4_____米.

15、矩形ABCD中，M是BC边上且与B、C不重合的点，点P是射线AM上的点，若以A、P、D为顶点的三角形与△ABM相似,则这样的点有　　 2　　　个.

三、(每小题8分，共16分)

16、如图，在△ABC中，D是BC上一点，∠CAD=∠B，BD=5，CD=4，求AC的长.

AC=6

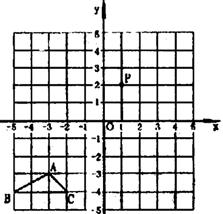
17、如图，在平面直角坐标系中，已知△ABC，点P（1，2）.

（1）作△PQR，使△PQR与△ABC相似（不要求写出作法）；

（2）在第（1）小题所作的图形中，求△PQR与△ABC的周长比.

略

四、(每小题9分，共18分)

18、如图在四边形ABCD中，DE∥BC，交AB于点E，点F在AB上，请你再添加一个条件（不再标注或使用其他字母），使△FCB∽△ADE，并给出出证明。

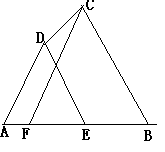你添加的条件是：　　　　　　　　　  。

证明：

添加的条件例举：FC∥AD，∠CFB=∠A，∠FCB=∠ADE，等　证明略.

19、如图，AD是Rt△ABC斜边上的高，DE⊥DF，且DE和DF分别交AB、AC于E、F.

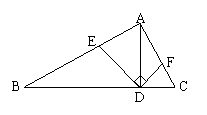求证：.

证明略

五、(每小题10分，共20分)

20、如图，已知△ABC、△DEF均为正三角形，D、E分别在AB、BC上。请找出一个与△DBE相似的三角形并证明。

△DBE、△ADG、△FHC都与△ECH相似 证明略

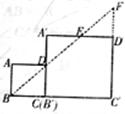
21、已知：如图，现有两个边长比为1∶2的正方形ABCD与A′B′C′D′，点B、C、B′、C′在同一直线上，且点C与点B′重合，请利用这两个正方形，通过截割、平移、旋转的方法，拼出两个相似比为1∶3的三角形.

要求：(1)借助原图拼图；(2)简要说明方法；(3)指明相似的两个三角形.

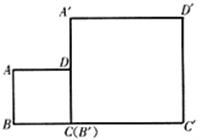方法：①连结BD并延长交A′D′于点E，交C′D′的延长线于点F；②将△DA′E绕点E旋转至△FD′E位置。则△BAD∽△FC′B，且相似比为1∶3.

六、(本题12分)

22、如图，△ABC中，D为AC上一点，CD＝2DA,∠BAC=45°，∠BDC=60°，CEBD，E为垂足，连接AE.

(1)写出图中所有相等的线段，并加以证明；

(2)图中有无相似三角形?若有，请写出一对；若没有，请说明理由；

(3)求△BEC与△BEA的面积之比.

(1)EC=EA=EB，DE=DA

(2)△ADE∽△CEA或△BCD∽△ACB

(3)2

七、(本题12分)

23、如图，△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC、CE、EG在同一直线上，且AB=，BC=1，连结BF，分别交AC、DC、DE于点P、Q、R.

（1）求证：△BFG∽△FEG，并求出BF的长；

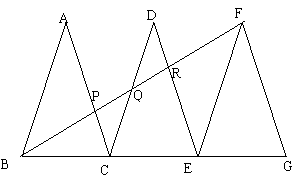（2）观察图形，请你提出一个与点P相关的问题，并解答（根据提出问题的层次和解答过程进行评分）。

(1)BF=3；

(2)A层次问题(较浅显的，仅用到了1个知识点)

例如：①求证：∠PCB=∠REC(或问∠PCB与∠REC是否相等？)等；

　　　②求证：PC∥RE(或问线段PC与RE是否平行？)等；

B层次问题(有一定思考，用到2~3个知识点)

例如：①求证：∠BPC=∠BFG(或BP=PR)等；②求证：△ABP∽△CQP等，△BPC∽△BRE等；③求证：△ABP∽△DQR等；④求BP∶PF的值等.

C层次问题(有深刻思考的，用到4个或4个以上知识点、或用到(1)中结论)

例如：①求证：△ABP≌△ERF；②求证：PQ=RQ等；③求证：△BPC是等腰三角形；④求证：△PCQ≌△RDQ等；⑤求AP∶PC的值等；⑥求BP的长；⑦求PC的长等.

证明略

八、(本题12分)

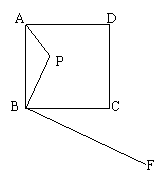24、如图，已知点P是边长为4的正方形ABCD内一点，且PB=3，BF⊥BP，垂足是B．请在射线BF上找一点M，使以点B、M、C为顶点的三角形与△ABP相似(请注意：全等图形是相似图形的特例) ．

在射线BF上取BM₁=或BM₂=3时，M₁，M₂都为符合条件的M．