海门实验学校九年级(下)数学期中试卷
考试时间：120分钟 总分：130分 命题人：许树荣
一．选择题（本大题共12题，每小题3分，共36分）下列各题的四个结论中只有一个是正确的 ，请将正确答案填入下表。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
1．sin30°的值是 （ ）
A．
B．
C．
D．1
2．抛物线y=(x–2)2的顶点坐标是 ( )
A．（2，0） B．（-2，0） C．（0，2） D．（0，-2）
3．如果⊙O1和⊙O2的半径分别为3cm和1cm，且O1O2=2cm．
则⊙O1和⊙O2位置关系是 ( )
A．外离 B．外切 C．相交 D．内切
4．二次函数y =x2的图像向上平移2个单位，得到新的图像的
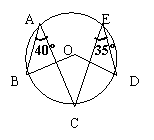二次函数表达式是
（ ）
A．y=x2–2 B． y=(x–2)2
C．y=x2+2 D． y=(x+2)2
5．图中∠BOD的度数是 ( )
A．75° B．80°
C．135° D．150°
6．半径为8的半圆是一个圆锥的侧面展开图，
那么这个圆锥的底面半径是（ ） (第5题图)
A．16 B．8 C．4 D．2
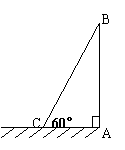
7．如图，一电线杆AB的高为10米，当太阳光线
与地面的夹角为60度时，其影子AC约为 （ ）
（
取1.732,结果保留3个有效数字）
A． 5.00米 B．8.66米
C．17.3米 D．5.77米 (第7题图)
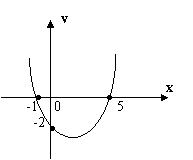
8．已知抛物线y =ax2+bx+c（a≠0）的图象如图所示，
则下列结论： （ ）
① a、b同号；
② 当x=1和x=3时，函数值相等；
初三数学第1页（共8页）
③ 4a+b = 0 ；
④ 当y = -2时，x的值只能取0
其中正确的个数是 （ ）
A． 1个 B． 2个 C． 3个 D． 4个
 |
|
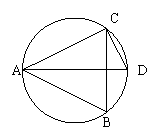
9．如图，已知AD是△ABC的外接圆的直径，AD=13cm，cosB= ，
则AC的长等于 （ ）
A．5cm B．6cm C． 10cm D．12cm
10．已知一次函数y =ax+c与二次函数y =ax2+bx+c，它们在同一坐标系内的大致图像是 （ ）
 |
A． B． C． D．
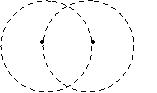
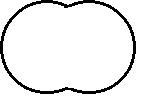
11．如图，实线部分是半径为9 m的两条等弧组成的游泳池。若每条弧所在的圆都经过另一个圆的圆心，则游泳池的周长为 （ ）
A．12πm B．18πm C．20πm D．24πm
 |
(第11题图) (第12题图)
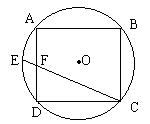
12．如图，⊙O是正方形ABCD的外接圆，F是AD的中点，CF的延长线交⊙O于E，那么CF∶EF的值是 （ ）
A．3∶1 B． 4∶1 C．5∶1 D．6∶1
初三数学第2页（共8页）
二．填空题（本大题共8题，每小题3分，共24分）
13．在Rt△ABC中，∠C=90°，tanA=, 则∠B=
．
14．抛物线y = x 2-4 x +5的对称轴是 ．
|
16．在Rt△ABC中，∠C=90°，AB=5，AC=3，则sinB=
．
(第15题图) (第17题图)
17．如图，⊙O的半径为1，PA切⊙O于点A，
且PA=2，则tan∠APO的值为 ．
18．一元钱硬币的直径约为24 mm，则它完全能
覆盖住的等边三角形的边长最大不能
超过 mm．（保留根号）
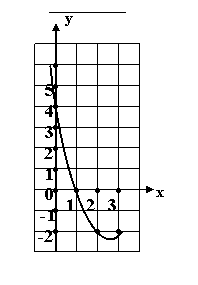
19．如图是某抛物线y =ax2+bx+c的部分图象，
有图象可知一元二次方程ax2+bx+c＝0的 (第19题图)
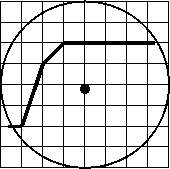两个解分别是 和
．
20．如图所示，圆被一条折线（图中粗线）
所分成的两部分面积之差为 ．
（网格由边长为1的正方形构成）
三．解答题（本题共10小题，共70分）
21．（本小题4分）计算：
cos30°+ sin45°
sin60°- cos45°
(第20题图)
22. （本小题6分）
已知圆锥侧面展开图的面积是15πcm2，母线的长是5cm．
⑴ 这个圆锥的底面半径是多少？
⑵ 在这个圆锥的底面上，有一点P，它到中心O的距离是1cm．
请找出过这一点到边缘两端的最长弦和最短弦的长
．
初三数学第3页（共8页）
23. （本小题6分）
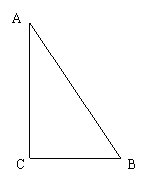
海门校服厂里有大量的剩余的三角形边角布料，现找出其中一种，测得AC=8cm,BC=6cm,AB=10cm（如图），现在要从这种三角形边角布料中剪出最大的圆，绣成海门实验学校的校徽．
⑴ 请你在下面备用的三角形中，设计出符合要求的圆的示意图．
（要求：尺规作图 ，不写作法，保留作图痕迹，作垂线可以用三角尺．）
⑵ 计算出这种布料绣成的校徽面积．（答案可带π）
 |
24. （本小题6分）
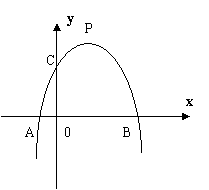
如图，抛物线y = - x2 +3x - n 经过点C（0，4），与x轴交于两点A、B．
⑴ 求抛物线的解析式；
⑵ 若点P是抛物线上位于x轴上方的一个动点，求△ABP面积的最大值．
 |
初三数学第4页（共8页）
25．（本小题6分）
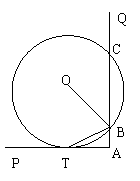
如图，∠PAQ是直角，半径为5的⊙O与AP相切与点T，与AQ交于两点B、C．
⑴ BT是否平分∠OBA？证明你的结论；
⑵ 若已知AT = 4，试求AB的长．
 |
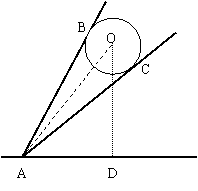
26. （本小题7分）
如图，挂着“庆祝海门实验学校建校三周年”条幅的氢气球升在校园上空，已知气球的直径为4m,在地面A点测得气球中心O的仰角为∠OAD=60°，测得气球的视角∠BAC=2°（AB、AC为⊙O的切线，B、C为切点）．
求气球中心O离地面的高度OD．
（精确到1m，参考数据：sin1°=0.0175,sin2°=0.0349,
tan1°=0.0175, tan2°=0.0350, =1.732 )
 |
初三数学第5页（共8页）
27．（本小题8分）
如图（单位：m），等腰直角三角形ABC以2m／s的速度沿直线L向正方形移动，直到AB与CD重合.设xs时，三角形与正方形重叠部分的面积为ym2.
⑴ 写出y与x的关系表达式.
⑵ 当x=2s，3.5s时，y分别是多少？
⑶ 当重叠部分的面积是正方形面积的一半时，三角形移动了
多长时间？
 |
28. （本小题8分）
有一圆弧形桥拱，水面AB宽32米，当水面上升4米后水面CD宽24米，此时上游洪水以每小时0.25米的速度上升，再通过几小时，洪水将会漫过桥面？
 |
初三数学第6页（共8页）
29．（本题9分）
某果园有100棵橙子树，每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵所接受的阳光就会减少。根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。假设果园增种x棵橙子树，果园橙子的总产量为y个．
⑴ 求果园增种橙子树x（棵）与果园橙子总产量y（个）的函数关系式．
⑵ 在上述问题中，果园要种多少棵橙子树，就可以使果园橙子的总产量为最多？
⑶ 增种多少棵橙子树时，可以使果园橙子的总产量在60420个以上？从计算结果和数学的角度看，你有什么感想（不超过30字）？
初三数学第7页（共8页）
30．（本题10分）
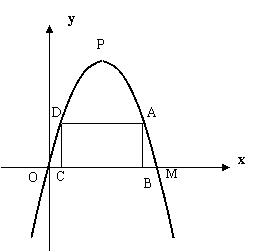
如图所示，在平面直角坐标系中，抛物线的顶点P到x轴的距离是4，抛物线与x轴相交于O、M两点，OM=4；矩形ABCD的边BC 在线段OM上，点A、D在抛物线上．
⑴ 请写出P、M两点的坐标，并求这条抛物线的解析式．
⑵ 设矩形ABCD的周长为L
① 当BC=2时，求矩形ABCD的周长；
② 矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值．
⑶ 连结OP、PM，则△PMO为等腰三角形，请判断在抛物线上是否还存在点Q（除点M外），使得△OPQ也是等腰三角形？若有，请在图上用尺规作图方法作出。
 |
初三数学第8页（共8页）