分类讨类思想
一：与线段有关的问题
1，线段AB=7cm，在直线上画线段BC=3cm，则线段AC=----
2，A，B两点到直线L的距离分别为m,n(m<n),则AB中点C到L的距离为----------------
二：与等腰三角形有关的问题
1．等腰三角形（直角三角形）的边角不确定性：
（1）．小芳要画-个有两边长分别为5cm和6cm的等腰三角形，则这个等腰三角形的周长是 ( )
（2）．等腰三角形的一个内角为70°，那么另两角是-------
（3）．等腰三角形的一个内角为70°，那么一腰上的高与底边所成的角等于--------
（4）．等腰ΔABC的底边BC=8且｜AC－ＢC｜=2，则腰AC的长为（ ）
A．10，6 B，10 C. 6 D.8, 6
（5）直角三角形的两边为3，4，则第三边为----------------
（6）.直角三角形的两条边长分别为6和8,那么这个三角形的外接圆半径等于 .
2．三角形高的位置
（1）等腰三角形一腰上的高与腰长之比为1：2，则等腰三角形的顶角为-------------
（2）等腰三角形一腰上的高等于该三角形某一条边长的一半，则其顶角度数为------------
二，与相似三角形有关的问题
（1）已知，ΔABC中，AB=8，AC=6，D点在AC上且AD=2，若在AE上找一点E，使ΔADE与原三角形相似，则AE=---
（2）RtΔABC中，∠C=90º ，BC=8，AC=6，则其内接正方形的边长为------------
（3）已知 ∠ABC= ∠CDB=90 º ，AC=a，BC =b，当BD与a, b间满足关系式----------------时，ΔABC与ΔCDB相似?
(4)△ABC是一块直角三角形余料，∠C＝90°．工人师傅要把它加工成一个正方形零件，使正方形的四个顶点在△ABC三边上．试画出你的设计方案，若AC＝80厘米，BC＝120厘米，请你计算出符合条件的最大正方形的边长．
三，与圆有关的问题
1一条弦所对的弧有两条，所对圆周角有2个。
1）
已知⊙o半径为6 cm, ⊙o的弦AB= cm,则弦AB所对的圆周角度数为------------
2） A,B是⊙o上两点，且∠AOB=70°,C是⊙o上不与A,B重合的任一点，则∠ACB=-------------------
3）
弦长是半径的 倍的弦所对的圆周角为------------
4）
如果圆中一条弦长与半径相等，那么此弦所对的圆周角的度数为____________________
5） ⊙o直径AB=4,弦AC= , AD= ,则∠DAC=---
6）
在⊙o中，弦AB将其分成3:7两部分，则该弦所对的圆周角度数为--------------
7）
若⊙o直径AB为2 ，弦AC为 ，弦AD为 ，则S扇形OCD（其中2S扇形OCD＜S扇形⊙o）为-----------
2点与圆的位置不同
1)点到⊙o的最长距离为5，最短距离为1，则圆的半径为—
2)⊙o和不在⊙o上的一点P，过点P的直线交⊙o于A,B两点，若PA·PB=24,OP=5,则⊙o半径为--------
3）如图：⊙O的直径为10cm，弦AB为8cm，P是弦AB上一点，若OP的长为整数，则满足条件的点P有（ ）个
3 弦和圆心的位置（圆内两条平行弦或相交两圆不同形式）
1） ⊙o半径为10cm，弦AB∥CD,AB=12cmCD=16cm,则AB和CD的距离为------cm，
2） 已知圆半径为10cm，它的内接梯形上下底分别为12cm和16cm，求梯形的高
3） 已知梯形ABCD内接于⊙o，AB∥CD，⊙o半径为5cm，AB=6cm，CD=8cm,则梯形ABCD的面积为------
4） ⊙o半径为5 cm，AB为直径，CD弦，CD⊥AB，垂足为E，若CD=6cm，则AE长为------------
5）
已知半径为4和 的两圆相交，公共弦长为4，则两圆的圆心距为-----
6） 已知⊙O1和⊙O2相交于A,B, 两圆的半径为 和 ,公共弦AB长为12，则∠O1AO2=---------------
4弓形的高
在半径为10的弓形中，弦长为12，则此弦长所对的弧所组成的弓形的高为-------
5圆周角与圆心角的位置
AB,AC与⊙o相切于B,C，∠A=50°,点P是圆上异于B,C的一动点，则∠BPC度数是-----
6两圆相切的不同形式或公切线的不同形式
1）点P在⊙o外，OP=13cm,PA切⊙o于A，PA=12cm以点P为圆心作⊙P与⊙o相切，则⊙P的半径为------
2）已知⊙O1和⊙O2外切, ⊙o1半径R=2,设⊙o2半径为r ,如果⊙O1和⊙O2公切线中有两条互相垂直，并且r=R,则r=----------
3）以O为圆心的两个同心圆的半径分别为11cm和9cm，若⊙P与这两个圆都相切，则⊙P的半径为------cm.
4）相切的两圆半径分别为3cm和2cm则两圆的圆心距为----
7利用旋转轴不同
1） 已知矩形两边长分别为5cm和2cm，求以一边所在直线为周旋转一周所得圆柱的表面积------------
2） 将两边分别为4cm和6cm的矩形，以其边所在的直线为轴旋转一周，所得圆柱表面积为--------
五．代数中的多解
1．比例中没讲谁前谁后 2． 参数方程的有解
3统计数据的不确定性
4 函数中的距离没有方向（上下或左右）
（1）一次函数y=x+b与x轴,y轴的交点分别为A,B，若ΔOAB的周长为 （O为坐标原点）,求b值
（2）已知直线y=x+3图象与x轴,y轴交于A,B两点，直线L经过原点,与线段AB交于点C,，把ΔAOB的面积分为2:1的两部分，求直线L的解析式。
（3）当m=-----时,函数y=(m+3)x2m+1+4x－５（x≠0）是一个一次函数
（4）直角坐标系中，有两点A(4,0).B(0,2)，如果点C在X轴上(C与A不重合)，当点C坐标为-----或------时，使得由B.O,C组成的三角形与ΔAOB相似。
（5）关于x的方程(m－2)x2－2有解，那么m的取值范围是------
（6）若二次三项式 m2—2(n+1)m+n+7是一个完全平方式，则n的值为------------------
(7)若方程kx2+x=3x2+1是一元二次方程,则k=---------
（8）一组数据5，7，7，x的中位数与平均数相等，则x=-----5,9-
(9) 如果四个整数数据中的三个分别是2、4、6，且它们的中位数也是整数，那么它们的中位数是 ．
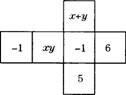
(10) 把如图折叠成正方体，如果相对面的值相等，则一组x、y的值是
（11）足球比赛的记分规则为：胜一场得3分，平一场得1分，输一场得0分.甲队比赛了5场后共得7分, 则甲队平了--------场。1，4
（12）某超市推出如下优惠方案：
1）一次性购物不超过100元不享受优惠。
2）一次性购物超过100元但不超过300元一律九折。
3）一次性购物超过300元一律八折。
王波两次购物分别付款80元，252元，如果王波一次性购买与上两次相同的商品，则应付款（ ）元。
（13）一次函数y=kx+b，当－３≤x≤１时，对应的 y值为１≤y≤９则kb的值为（ ）
A, 14 B.－６ Ｃ,－４或２１ Ｄ,－６或１４
（14） 若抛物线y=x2---(a+2)x+9的顶点在坐标轴上，求 a的值