中考模拟考试数学卷2

中考模拟考试数学卷2

数　学　试　卷

　　　　　　　  (说明：全卷共8页。考试时间为90分钟，满分120分。)

得分	评卷人

　　　　　

一、选择题（本题共5小题，每小题3分，共15分。每小题给出的4个选项中只有一个是正确的，请将所选选项的字母写在题目后面的括号内）

1. 我国现有人口约为，用科学记数法表示并将结果保留3位有效数字为　　 （　　　）.

A. 1.29×10¹⁰  B. 1.3×10¹⁰

 C. 1.30×10¹⁰ D. 1.30×10⁹

2.  下列运算正确的是　　　　　　　　　　　　　　　　　　　　　　  （　　　 ）.

A.  B. 

 C.　 D.　

3. 下列各数中，互为相反数的是　　　　　　　　　　　　　　　　　　　 （　　　）.

A. B. 

 C D.　

4. 如图O为圆心，∠AOB=130°，C是AB弧上任意一点，则∠ACB=　　　　　　　 （　　　）.

A.  135°　　　　　　　　　　　　 

B.  130°　　　　

C.  115°　　　　

第4题图

D.　 50°

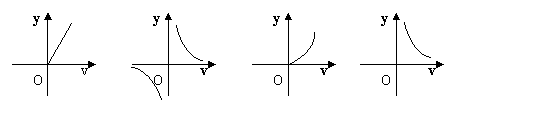
5. 已知甲、乙两地相距120千米，汽车从甲地匀速行驶到乙地。如果每小时耗油为5升，那么从甲地到乙地汽车总耗油量y（升）与汽车行驶的速度v（千米/时）的函数关系的图象为　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　）.

B

D

A

C

得分	评卷人

二、填空题 （本题共5小题，每小题4分，共20分。请将下列各题的正确答案填写在横线上）

6. 函数中自变量x的取值范围是　　　　　　 。

7. 请你写出一个二次项系数为1，两实根之和为3的一元二次方程　　　　　　　  。

8. 已知⊙O₁、⊙O₂的半径分别为4和2，且⊙O₁与⊙O₂相切，则O₁O₂的长为　　　　 。

9. 如图⊙O₁、⊙O₂是半径为1的两等圆，O₁在⊙O₂上，图中阴影部分的面积为　　　 。

　

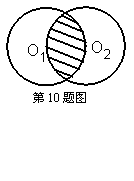10. 观察下列顺序排列的等式：，…猜想：第n个等式（n为正整数）应为　　　　　　　　　　　　  。

得分	评卷人

三、解答题 （本题共5小题，每小题6分，共30分）

11. 先将化简，然后自选一个合理的值代入求值。

12. 解不等式组，并将解集在数轴上表示出来

　　　

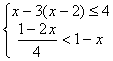
13. 解方程组：

　　　

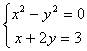
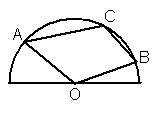
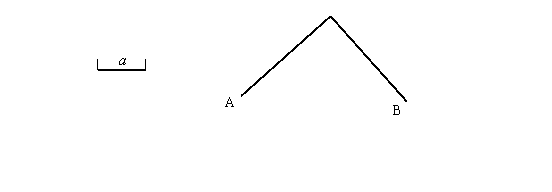
14. 如图：AO、BO是两条互相垂直的公路，为方便汽车行驶，计划修一段半径为的圆弧弯道将它们连接起来。请你用直尺和圆规在图中画出圆弧弯道。（不写作法和证明，但要保留作图痕迹）　　　　　　　

O

15. 已知二次函数经过（1，0），（0，3）两点

（1）求此二次函数解析式；

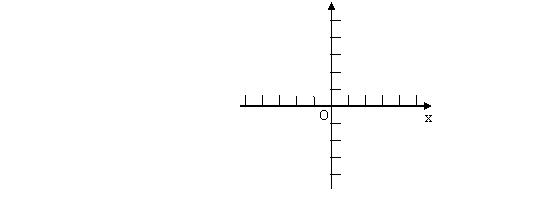
（2）在所给的直角坐标系中画出此二次函数当时的图象。

　　　　　　　　　　　　　　  　　　　　　　　　 

y

　　　　　　　　　　　　　　　　　　　　　  　　　 　　　 　　　 　　　

得分	评卷人

四、解答题 （本题共4小题，每小题7分，共28分）

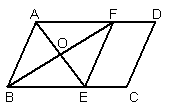
16. 如图：在□ABCD中，E为BC上一点，O为AE的中点，BO的延长线交AD于F

　　（1）求证：△AOF≌△EOB；

　　（2）若∠ABF=∠EBF，试判断四边形ABEF的形状，并加以证明。

第16题图

　　

17. 在某中学举办的电脑知识竞赛中，将初三年级学生成绩（得分均为整数）抽样并对其整理后分成五组，绘制出如图所示的频率分布直方图。已知图中从左到右的第1、第3、第4、第5组的频率分别是0.30、0.15、0.10、0.05，第2组的频数是40

分数

99.5

89.5

49.5

59.5

69.5

79.5

　

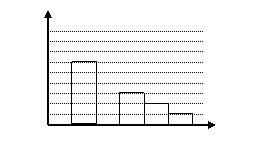
（1）第2组的频率为　　　，在此问题中样本容量为　　　　，样本的中位数落在第　　　组；

（2）在图中补全频率分布直方图；

（3）若得分在80分以上（含80分）为优秀，试估计全校600名初三学生中成绩优秀的有多少人？

18. 一列火车已经晚点6分钟，如果将速度每小时加快10千米，那么火车继续行驶20千米便可正点运行，求火车原来的速度。

.

.

19. 如图1，将射线Ox按逆时针方向旋转α角，得到射线Oy，如果点P为射线Oy上一点，且OP=a，那么我们就规定用（a，α）表示点P在平面内的位置，并记作P（a，α）。例如，如图2中，如果OM=8，∠xOM=100°，那么点M在平面的位置记为M（8，100°）。

根据上面的材料解答下列问题：

M(8，100°)

图4

O

O

O

图3

图2

图1

A(4，45°)

x

x

x

O

x

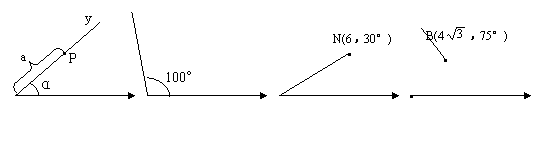
（1）在图3中，如果点N在平面内的位置记为（6，30°），那么ON=　　　　，

∠xON=　　　　 。

（2）在图4中，如果点A、B在平面的位置分别记为A（4，45°）、B（75°），

试求A、B两点的距离.

得分	评卷人

五、解答题 （本题共3小题，每小题9分，共27分）

20.已知关于x的方程。

（1）求证：此方程一定有两个不相等的实数根；

（2）若是方程的两实数根，且，求k的值。

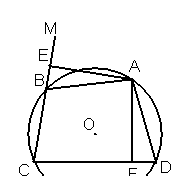
21. 如图：四边形ABCD内接于⊙O，AD=AB，E为CB延长线BM上一点.

（1）　　　 如果AE⊥BM，过A作AF⊥CD，垂足为F①求证：BE=DF；②设CD=21，AD=AB=10，BC=9，求对角线AC的长.

（2）　　　 如果题设条件不变，当E点在BM上运动到某一位置满足一定条件时，就有AB·DA=BE·CD成立.问该结论成立的条件是什么？请注明条件，并给出证明。

　　　

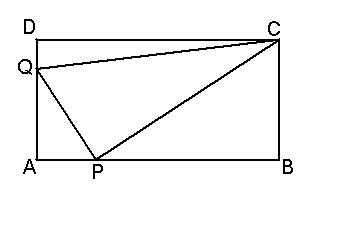
22. 如图：在矩形ABCD中，AB=12，BC=6，点P沿AB从点A开始向点B以每秒2个单位长度的速度移动，点Q沿DA从点D开始向点A以每秒1个单位长度的速度移动。若P、Q同时出发，用t（秒）表示移动时间（0≤t≤6）

（1）　　　 设△PQC的面积为S，求S与t的函数关系式；

（2）　　　 在P、Q移动过程中，是否存在t ，使△PQC为直角三角形？若存在，求出此时的t ；若不存在，说明理由。

（3）　　　 若P移动到B ，Q移动到A后立即返回，且0≤t≤12。在此过程中，使△PQC为直角三角形的t值有几个？请直接写出t 值的个数 ，不需说明理由。