北师大版九年级数学《二次函数》测试
姓名 班级
（时间：100分钟，总分：100分）
一、填空题(每小题2分，共16分)
1、抛物线y=
(x+3)2的开口方向
，顶点坐标是______.
2、已知抛物线y=－2(x+1)2－3，如果y随x的增大而减小，那么x的取值范围是______.
3、如图1所示的抛物线：当x<－2或x>0时， y_____0；当x在_____范围内时，y>0。
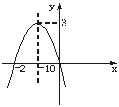
图1
4、已知函数y=
，当k=______时，它的图象是开口向下的抛物线；此时当x______时，y随x的增大而减小.
5、二次函数y=－
x2，当x1<x2<0时，y1与y2的大小为______.
6、在边长为6 cm的正方形中间剪去一个边长为x cm(x<6)的小正方形，剩下的四方框形的面积为y，y与x之间的函数关系是______.
7、写出一个开口向上，顶点是坐标原点的二次函数的表达式：______.
8、小立存入银行人民币500元，年利率为x%，两年到期，本息和为y元(不含利息税)，y与x之间的函数关系是_______，若年利率为6%，两年到期的本利共______元.
二、选择题(每小题2分，共24分)
9、抛物线y=x2+1的图象大致是
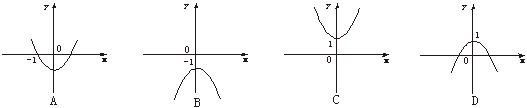
10、函数y=x2+2x+1写成y=a(x－h)2+k的形式是
A.y=(x－1)2+2 B.y=(x－1)2+
C.y=(x－1)2－3 D.y=(x+2)2－1
11、若函数y=4x2+1的函数值为5，则自变量x的值应为
A.1
B.－1 C.±1
D.
12、抛物线y=－2x2－x+1的顶点在第_____象限
A.一 B.二 C.三 D.四
13、抛物线y=x2向左平移3个单位，再向下平移2个单位后，所得的抛物线表达式是
A.y=(x+3)2－2
B.y=(x－3)2+2
C.y=(x－3)2－2
D.y=(x+3)2+2
14、二次函数y=(3－m)x2－2mx－m的图象如图2所示，则m的取值范围是
A.m>0 B.m<0 C.m<3 D.0<m<3
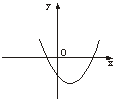
图2
15、不论m取任何实数，抛物线y=a(x+m)2+m(a≠0)的顶点都
A.在y=x直线上 B.在直线y=－x上
C.在x轴上 D.在y轴上
16、下列函数中，具有过原点，且当x>0时，y随x增大而减小这两个特征的有
①y=－ax2(a>0) ②y=(a－1)x2(a<1) ③y=－2x+a2(a≠0) ④y=
x－a
A.1个 B.2个 C.3个 D.4个
17、下列说法错误的是
A.二次函数y=3x2中，当x>0时，y随x的增大而增大
B.二次函数y=－6x2中，当x=0时，y有最大值0
C.a越大图象开口越小，a越小图象开口越大
D.不论a是正数还是负数，抛物线y=ax2(a≠0)的顶点一定是坐标原点
18、在同一坐标系中，作y=x2，y=－x2，y=
x2的图象，它们的共同特点是
A.抛物线的开口方向向上
B.都是关于x轴对称的抛物线，且y随x的增大而增大
C.都是关于y轴对称的抛物线，且y随x的增大而减小
D.都是关于y轴对称的抛物线，有公共的顶点
19、如图3，函数y=－a(x+a)与y=－ax2(a≠0)在同一坐标系上的图象是
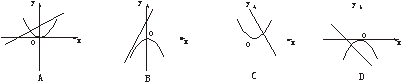
图3
20、已知a<－1，点(a－1，y1)，(a，y2)(a+1，y3)都在函数y=x2的图象上，则
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
三、解答题(共16分)
21、(5分)已知一次函数y=－2x+c与二次函数y=ax2+bx－4的图象都经过点A(1，－1)，二次函数的对称轴直线是x=－1，请求出一次函数和二次函数的表达式.
22、(5分)正方形的边长为1 cm，假设边长增加x cm时，正方形的面积增加y cm2.
(1)请写出y与x之间的关系表达式;
(2)当正方形边长分别增加1
cm，
cm，2 cm时，正方形的面积增加多少？
23、(6分)二次函数y=ax2与直线y=2x－1的图象交于点P(1，m).
(1)求a、m的值;
(2)写出二次函数的表达式，并指出x取何值时，该表达式的y随x的增大而增大.
四、生活中的数学(共28分)
24、(6分)当一枚火箭被竖直向上发射后，它的高度h(m)与时间t(s)的关系可以用公式h=－5t2+150t+10表示.经过多长时间，火箭到达它的最高点？最高点的高度是多少？
25、(7分)把8米长的钢筋，焊成一个如图4所示的框架，使其下部为矩形，上部为半圆形.请你写出钢筋所焊成框架的面积y(平方米)与半圆的半径x(米)之间的函数关系式
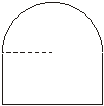
图4
26.(7分)影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数.有研究表明，晴天在某段公路上行驶时，速度v(km/h)的汽车的刹车距离s(m)可以由公式s=
v2确定；雨天行驶时，这一公式为s=
v2.
(1)如果行车速度是70 km/h，那么在雨天行驶和在晴天行驶相比，刹车距离相差多 少米？
(2)如果行车速度分别是60 km/h与80 km/h，那么同在雨天行驶(相同的路面)相比，刹车距离相差多少？
(3)根据上述两点分析，你想对司机师傅说些什么？
27、(8分)有一座抛物线形拱桥，桥下面在正常水位时AB宽20米，水位上升3米就达到警戒线CD，这时水面宽度为10米;
(1)在如图5的坐标系中，求抛物线的表达式.
(2)若洪水到来时，再持续多少小时才能到拱桥顶？(水位以每小时0.2米的速度上升)
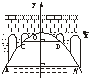
图5
五、探究拓展与应用(共16分)
28、(6分)观察图6中正六边形“蜘蛛网”的变化规律：
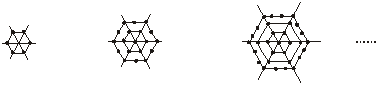
图6
(1)完成下表：
| 边上的小点数 | 1 | 2 | 3 | 4 | 5 |
| 小点的总数 |
(2)如果用n表示六边形边上的小点数，m表示这个正多边形中小点的总数，那么m和n的关系是什么？
29、(10分)如图7，直线AB过x轴上的点A(2，0)，且与抛物线y=ax2相交于B、C两点，B点坐标为(1，1).
(1)求直线和抛物线所表示的函数表达式;
(2)在抛物线上是否存在一点D，使得S△OAD=S△OBC，若不存在，说明理由；若存在，请求出点D的坐标。.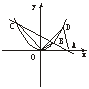 
图7