九年级数学第一学期期末试卷3
一、填空题(每空3分，共24分)
1.
代数式：
中， 是分式
2.
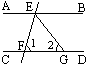两地实际距离时45000米，在地图上的距离是5cm，则这张地图的比例尺是
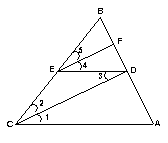
3. 如图，AB∥CD，直线EF分别交AB、CD于E、F，EG平分∠BEF,若∠1=720，则∠2=
4. 已知一个样本容量为40，把它分成六组，第一组到第四组的频数分别为10、5、7、6，第五组的频率是0.10，则第六组的频率是
5. 如图，△ABC∽△ACD,若AD=5,BD=4,则△ACD与△ABC的相似比为
6.
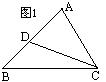已知不等式组
的整数解是
7.
但m= 时，方程
产生增根
8.
样本
的方差为
，则
的方差为
二、 选择题(每小题3分，共30分)
1.
把多项式
分解因式 ( )
A.
； B.
； C.
； D.
2. 能使△ABC∽△DEF的条件是 ( )
A. ∠C=980
, ∠B=980 , 
B. AB=1, AC=1.5, BC=2, EF=8, DE=10, FD=16
C. ∠A=∠F=900, AC=5, BC=13, DF=10, EF=26 D. ∠A=460, ∠B=540, ∠E=540, ∠F=800
3.
化简
的结果是 (
)
A. 
B. 
C.
D.
4.
样本
的方差是 ( )
A. 2
B. 4
C. 
D.
5
5. 已知线段AB=1, 点C、D是线段AB上的两个黄金分割点，则CD的长是：( )
A.
B.
C.
D. 
6. 下列语句中正确的是 ( )
A.三角形的外角大于它的内角； B. 三角形的一个外角等于它的两个内角和
C. 三角形的一个内角小于和它不相连的外角 D. 三角形的外角和等于1800
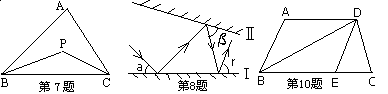
7. 如图，P是△ABC的内角平分线的交点，∠BPC=1200, 则∠A= ( )
A. 300 B. 450 C. 600 D. 700
8.
如图所示，光线L照射到平面镜Ⅰ上，然后再平面镜Ⅰ、Ⅱ之间来回反射，已知
，则
的度数为 ( )
A. 500 B. 550 C. 600 D. 650
10. 如图，在梯形ABCD中，AD∥BC, ∠ADB=∠CDE, 且BD : DE=2 : 1，则△BDE的面积与△DEC的面积比为 ( ) A. 2:1 B. 5:2 C. 3:1 D. 4:1
三、解方程或化简(每题6分，共18分)
⑴ 
⑵ 
⑶ 
四、解不等式(组)并把它们的解集在数轴上表示出来(每题8分，共16分)
⑴ 
≥
⑵
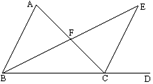五、证明题(10分) 如图，∠ACD是△ABC的外角，BE平分∠ABC,
CE平分∠ACD,且BE、CE相交于E。求证：
=
六、(10分)甲、乙两班举行电脑汉字输入速度比赛，各选10名学生参加，各班参赛学生每分钟输入汉字个数统计如下表：
| 输入汉字(个) | 132 | 133 | 134 | 135 | 136 | 137 | 众数 | 中位数 | 平均数 | 方差 |
| 甲班学生(人) | 1 | 0 | 1 | 5 | 2 | 1 | 135 | 135 | 135 | 1.6 |
| 乙班学生(人) | 0 | 1 | 4 | 1 | 2 | 2 |
请你填写表格中乙班学生的相关数据，再根据所学统计知识，从不同方面评价甲、乙两班学生的比赛成绩（至少从两个方面进行评价）
七、(12分)
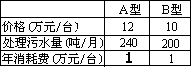
为了保护环境，某企业决定购买10台污水处理设备，现有A、B两种型号的设备，其中每台价格，月处理污水量极消耗费如下表：
经预算，该企业购买设备的资金不高于105万元
⑴ 请你为企业设计几种购买方案
⑵ 若企业每月产生污水2040吨，为了节约资金，应选那种方案？
24、看图填空：
（1） 
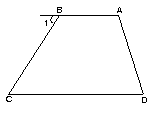如图，∠A＋∠D＝180º（已知）
∴ ∥ （ ）
∴∠1＝ （ ）
∵∠1＝65º（已知）
∴∠C＝65º（ ）
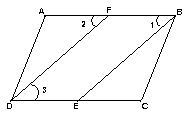
（2）如图，已知，∠ADC＝∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2，求证：∠A=∠C.
证明：∵BE、DF分别平分∠ABC、∠ADC（已知）
∴ ∠1＝
∠ABC，∠3＝∠ADC（ ）
∵∠ABC＝∠ADC（已知）
∴∠ABC＝∠ADC（
）
∴∠1＝∠3（ ）
∵∠1＝∠2（已知）
∴∠2＝∠3（ ）
∴（ ）∥（ ）（ ）
∴∠A＋∠ ＝180º ，∠C＋∠ ＝180º（ ）
∴∠A＝∠C（ ）
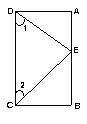
25、如图：已知CB⊥AB，CE平分∠BCD，DE平分∠ADC，∠1＋∠2＝90º
求证：AB∥CD
26、如图，已知：AC∥DE，DC∥EF，CD平分∠BCA
求证：EF平分∠BED.
