九年级数学期末测试
1、为了充分利用我国丰富的水力资源，国家计划在四川省境内的长江上游修建一系列大型水力发电站，这些水力发电站的年发电总量相当于是10座三峡电站.因此，四川省境内的这些水力发电站的年 发电总量可达到千瓦时，把它用科学记数法表示为（ ）.
A、8.47×1011千瓦时 B、847×109千瓦时
C、8.47×1010千瓦时 D、0.847×1012千瓦时
2、下列各式中运算正确的是（ ）
（A）=x3 （B）= （C）= 0 （D）=1
3、 如果分式的值为零，那么x的值为（ ）.
（A）0 （B）±1 （C） -1 （D）1
4、下列分式一定有意义的是（ ）.
（A） （B） （C） （D）
5、（7）下列各式中正确的是（ ）
（A）
（B）
（C）
（D）
6. 如果分式 的值是正数，那么a的取值范围是（ ）
（A）a>2 （B）a≧ （C）a＜ （D）a>
7、方程
的根的情况是：
A. 有两个不相等的实数 B. 有两个相等的实数 C.没有实数根
8、已知关于x的方程
有实数根，则k的取值范围是：
A. 
B.
C.
D.
9、下列一元二次方程中，两个实数根的和为3的方程是：
A.
B.
C.
D.
10、某商场的的营业额1998年比1997年上升10%，1999年比1998年上升10%，而2000年和2001年连续两年平均每年比上一年降低10%，那么2001年的营业额比1997年的营业额（ ）
A．降低了2% B.没有变化 C.上升了2% D.降低了1.99%
二、填空
1、 当x= 时，分式没有意义.
2、当m 时，关于x的一元二次方程x2－2x+m=0有两个实数根
3、以2+
和2－为两根的一元二次方程是
4、某工厂第一季度平均每月增产率10%,已知一月份的产值是a万元,第一季度的总产值是 万元。
5、方程
有两个正实根，则数m的取值范围
三，计算
1、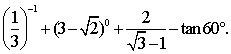
（本题4分）
2、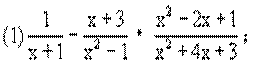
3、已知一元二次方程
，求当k为何值时，方程有两个不相等的实数根？（本题5分）
4、已知关于x的一元二次方程
(1)求证:不论k为何值,方程总有两个不相等的实数根
(2)设x1,x2是方程的两根,且
求k的
5、
三、应用题
1、华联商场销售部经理“老夫子”在设计促销方案。“老夫子”提出了Ａ、Ｂ、Ｃ三个方案，购物满２００元，可以掷两次骰子，根据两次骰子的总点数决定送礼券多少。
Ａ方案：总点数是几就送礼券几十元。
Ｂ方案：总点数为中间数７时的礼券最多，为１２０元；以此为基准，总点数每减少或增加１，礼券减少２０元。
Ｃ方案：总点数为２和１２时的礼券最多，都为１２０元；点数从２到７递增或从１２到７递减时，礼券都依次减少２０元。
你选择哪一个方案，可以使赠送的金额比较诱人，但顾客拿走的机会又比较小。请说明理由。（本题4分）
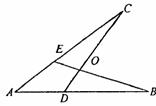
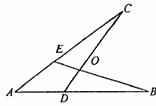2、如图，下面四个条件中，请你以其中两个为已知条件，第三个为结论，推出一个正确的命题（只需写出一种情况）.①AE = AD ②AB = AC ③OB = OC ④∠B=∠C（本题4分）
