九年级数学期末考试试题
数 学 试 卷
(考试时间120分钟 满分120分)
一．填空题（本大题10小题，每小题2分，共20分）
1. 
.
2. 因式分解：
3. 在△ABC中，∠B＝25°，AD是BC边上的高，并且
，则∠BCA的度数为_______65°或115°_____
4. 不等式组
的解集是____
________
5. 甲、乙两人进行射击比赛，在相同条件下各射击 10 次他们的平均成绩均为 7 环10 次射击成绩的方差分别是：
，
．成绩较为稳定的是____乙______．（填“甲”或“乙” ）
6. 在函数
中，自变量x的取值范围是______
______
7. 若关于x的一元二次方程
有实数根，则k的取值范围是D___________
8. 张老师在一次“探究性学习”课中，设计了如下数表：
| n | 2 | 3 | 4 | 5 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | … |
| b | 4 | 6 | 8 | 10 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | … |
（1） 请你分别观察a、b、c与n之间的关系，并用含自然数n (n>1)的代数式表示：
a = ，b = ，c = .
9. 某同学在电脑中打出如下排列的若干个圆（图中●表示实心圆，○表示空心圆）：
● ○●●○●●●○●●●●○●●●●●○●●●●●●○
若将上面一组圆依此规律复制得到一系列圆，那么前2005个圆中有 个空心圆
 |
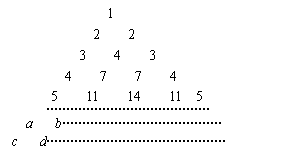10. 右图是与杨辉三角有类似性质的三角形数垒，
是相邻两行的前四个数（如图所
示）．那么当
时，
．
．
二．选择题（本大题8小题，每小题3分，共24分）每小题都给出代号为A，B，C，D的四个结论，其中只有一个是正确的，选择正确结论的代号填在括号内。
11. 分式
计算的结果是（ ）
(A)
(B)
(C)
(D)
12. 中央电视台“开心辞典”栏目有这么一道题：小兰从镜子中看到
挂在她背后墙上的四个时钟如下图所示，其中时间最接近四点钟
的是（ ）
 |
(A) (B) (C) (D)
13. 足球比赛的计分规则为：胜一场得3分，平一场得1分，负一场得0分，一个队进行了14场比赛，得分不低于20分，那么该队至少胜了几场（ A ）
A.3 B.4 C.5 D.6
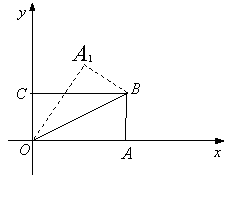14. 如图，在直角坐标系中，将矩形
沿
对折，使点
落在点
处已知
,
，则点的坐标是（ A ）．
A．（
，
） B．（，3）
C．（，） D．（
，）
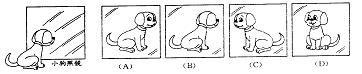
15. 一只小狗正在平面镜前欣赏自己的全身像（如图所示），此时，它所看到的全身像是( A )
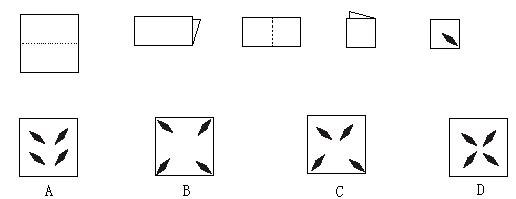
16. 如图，将一张正方形纸片经两次对折，并剪出一个菱形小洞后展开铺平，得到的图形是（ ）
17. 根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
|
| －0.06 | －0.02 | 0.03 | 0.09 |
判断方程
(a≠0，a，b，c为常数)一个解x的范围是（ C ）
A、3＜x＜3.23 B、3.23＜x＜3.24
C、3.24＜x＜3.25 D、3.25 ＜x＜3.26
18. 我们从不同的方向观察同一物体时，可以看到不同的平面图形，如图，从图的左面看这个几何体的左视图是B
 | |||||||||
 |  | ||||||||
 | |||||||||
 | |||||||||
A B C D
三．（本大题共2小题，每小题8分，满分16分）
19．计算：
20．解方程：
四、（本题Ａ类题满分７分，Ｂ类题满分10分）
21．本题有Ａ、Ｂ两类题．Ａ类题满分7分，Ｂ类题满分10分．请你选择其中一类证明．
（Ａ类）如图９，
．垂足分别为
．请你从下面三个条件
中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题（只需写出一种情
况）．
①
②
③
已知：，垂足分别为， ＝ ， ＝ ．
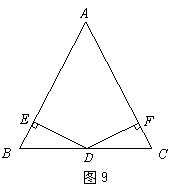求证：
证明：
（Ｂ类）如图10，
，请你从下面三个条件中，再选两个作为已知条件，另
一个为结论，推出一个正确的命题（只需写出一种情况）．
① ②
③
已知：， ＝ ， ＝ ．
求证：
证明：
五、（本大题共4小题，每小题10分，共40分）
22．如图11，石头和石头
相距80cm，且关于竹竿l对称，一只电动青蛙在距竹竿30cm，
|
|
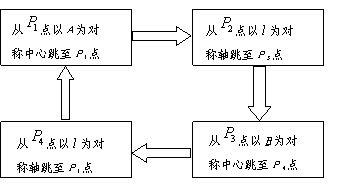距石头Ａ为60cm的
处，按如下顺序循环跳跃：
 | |||||
 | |||||
 | |||||
（１）
|
（２）
青蛙跳跃25次后停下，此时它与石头相距
cm，与竹竿
相距 cm．
23．南宁市是广西最大的罗非鱼养殖产区，被国家农业部列为罗非鱼养殖优势区域．某养
殖场计划下半年养殖无公害标准化罗非鱼和草鱼，要求这两个品种总产量
（吨）满
| 品种 | 单价（万元/吨） |
| 罗非鱼 | 0.45 |
| 草鱼 | 0.85 |
足：
，总产值为1000万元．
已知相关数据如右表所示．
求：该养殖场下半年罗非鱼的产量应控制在什么
范围？（产值＝产量
单价）
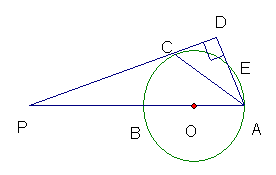24. 已知，AB为⊙O 的直径，点E 为弧AB 任意一点，如图，AC平分∠BAE,交⊙O于C ,过点C作CD⊥AE于D,与AB的延长线交于P
⑴ 求证：PC是⊙O的切线。
⑵ 若∠BAE=60°，求线段PB与AB的数量关系。
25. 某市城建部门经过长期市场调查发现，该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x；年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=
―10；
(1)如果年新建商品房的面积与年新房销售面积相等，求市场新房均价和年新房销售总额；
(2)在(1)的基础上，如果市场新房均价上涨1千元，那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况，请你提出一条合理化的建议。(字数不超过50)
26. 某学校对初中毕业班经过初步比较后，决定从初三（1）、（4）、（8）班这三个班中推荐一个班为市级先进班集体的候选班.现对这三个班进行综合素质考评，下表是它们五项素质考评的得分表（以分为单位），每项满分为10分）.
| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 初三（1）班 | 10 | 10 | 6 | 10 | 7 |
| 初三（4）班 | 10 | 8 | 8 | 9 | 8 |
| 初三（8）班 | 9 | 10 | 9 | 6 | 9 |
（1）请问各班五项考评分的平均数、中位数和众数中哪个统计量不能反映三个班的考评结果的差异？并从中选择一个能反映差异的统计量将他们得分进行排序；
（2）根据你对表中五个项目的重要程度的认识，设定一个各项考评内容的占分比例（比例的各项须满足：①均为整数；②总和为10；③不全相同），按这个比例对各班的得分重新计算，比较出大小关系，并从中推荐一个得分最高的班级作为市级先进班集体的候选班.