新课标(北师大版)中考数学第一轮复习测试卷
第十二单元生活中的平移、旋转和对称图形
一、选择题(每小题4分，共40分)
1、在下面五幅图案中，(2)、(3)、(4)、(5)中哪一幅图案可以通过平移图案(1)得到.（ B ）
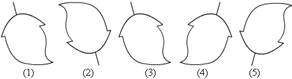
A.(2) B.(3) C.(4) D.(5)
2、在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转.下列图案中，不能由一个圆形通过旋转而构成的是（ C ）
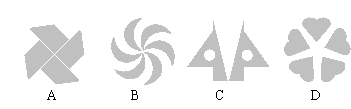
3、下列各图中，既是轴对称图形又是中心对称图形的是（ C ）
 |
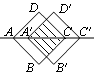
4、把正方形ABCD沿着对角线AC的方向平移到正方形A′B′C′D′的位置，它们的重叠部分(图中的阴影部分)的面积是正方形ABCD面积的一半，若AC=
，则正方形平移的距离AA′是（ D ）.
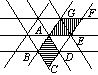
A.1 B.
C.
D.
 |
(第4题图) (第5题图) (第6题图) (第7题图)
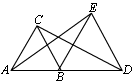
5、如图，△ABC与△BDE都是等边三角形，AB<BD。若△ABC不动，将△BDE绕Ｂ点旋转，则在旋转过程中，AE与CD的大小关系为（ A ）
A.AE=CD B.AE>CD C.AE<CD D.无法确定
6、同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一个图案，图中所有小三角形均是全等的等边三角形，其中的菱形AEFG可以看成是把菱形ABCD以A为中心（ C ）
A.顺时针旋转60°得到 B.顺时针旋转120°得到
C.逆时针旋转60°得到 D.逆时针旋转120°得到
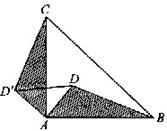
7、如图，D是等腰Rt△ABC内一点，BC是斜边，如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置，则∠ADD′的度数是（ D ）
A.25° B.30° C.35° D.45°
8、已知∠AOB=30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1，O，P2三点所构成的三角形是（ D ）
A．直角三角形 B．钝角三角形 C．等腰三角形 D．等边三角形
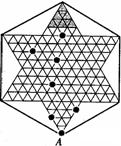
9、如图是一跳棋盘，其中格点上的黑色点为棋子，剩余的格点上没有旗子。我们约定跳棋游戏的规则是：把跳棋旗子在棋盘内沿直线隔着旗子对称跳行，跳行一次称为一步。已知点A为已方一枚旗子，欲将旗子A跳进对方区域(阴影部分的格点)，则跳行的最少步数为（ B ）
A.2步 B.3步 C.4步 D.5步
 |
(第9题图) (第10题图)
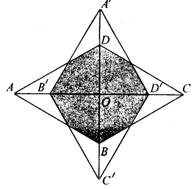
10、如图，菱形纸片ABCD的一内角为60°．边长为2，将它绕对角线的交点O顺时针旋转90°后到A′B′C′D′ 位置，则旋转前后两菱形重叠部分多边形的周长为（ C ）
A.8 B.4(
－1) C.8(－1) D.4(＋1)
二、填空题(每小题4分，共20分)
11、在你所学过的几何图形中，写出两个既是轴对称图形又是中心对称图形的图形名称：__比如矩形、正方形、菱形、圆等_____.
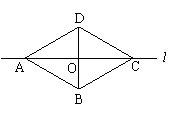
12、如图，直线l是四边形ABCD的对称轴，若AB=CD，有下面的结论：①AB∥CD；②AC⊥BD；③OA=OC；④AB⊥BC。其中正确的结论有 ①②③ (填序号).
 | |||||
 | |||||
 | |||||
(第12题图) (第13题图) (第14题图)
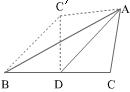
13、如图，AD是ΔABC的中线，∠ADC=45°，把ΔADC沿AD对折，点C落在点C′的位置，则BC′与BC之间的数量关系是 BC′=
BC .
14、如图是两张全等的图案，它们完全重合地叠放在一起，按住下面的图案不动，将上面图案绕点O顺时针旋转，至少旋转 60 度角后，两张图案构成的图形是中心对称图形.
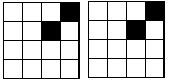15、由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑(如右图)。请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑，使它成为轴对称图形。
略
三、(每小题8分，共16分)
16、如图，AM//DN，直线l与AM、DN分别交于点B、C. 在线段BC上以一点P，直线l绕点P旋转.请你写出变化过程中直线l与AD、AM、DN围成的图形的名称.（至少写出三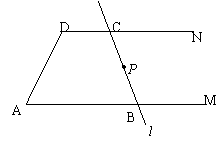
个）
三角形、一般梯形、等腰梯形、直角梯形、平行四边形等
17、如图，在10×5的正方形网格中，每个小正方形的边长均为单位1，将△ABC向右平移4个单位，得到△A′B′C′，再把△A′B′C′绕点A′逆时针旋转90°，得到△A″B″C″.请你画出△A′B′C′和△A″B″C″（不要求写画法）
 |
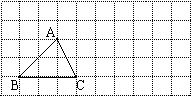图略
四、(每小题9分，共18分)
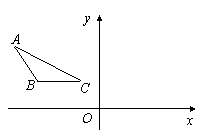
18、已知：如图，在△ABC中，AB=BC=2，∠ABC=120°，BC∥x轴，点B的坐标是（-3，1）.
(1)画出△ABC关于y轴对称的△A′B′C′；
(2)求以点A、B、B′、A′为顶点的四边形的面积.
 |
(1)图略
(2)7
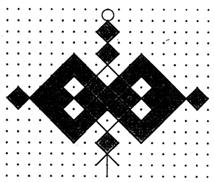
19、如图是一个在19×16的点阵图上画出的“中国结”，点阵的每一行及每列之间的距离都是1，请你画出“中国结”的对称轴，并直接写出图中阴影部分的面积.
 |
略
五、(每小题10分，共20分)
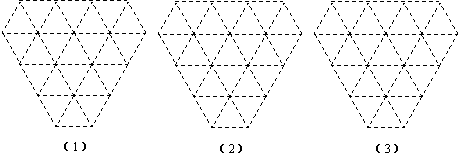
20、请你在下面3个网格（两相邻格点的距离均为1个单位长度）内，分别设计1个图案，要求:在(1)中所设计的图案是面积等于的轴对称图形；在（2）中所设计的图案是面积等于2的中心对称图形；在（3）中所设计的图案既是轴对称图形又是中心对称图形，并且面积等于3．将你设计的图案用铅笔涂黑．
 |
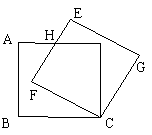21、如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H，求DH的长.
|
六、(本题12分)
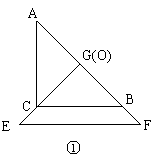22、把两个全等的等腰直角三角形ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转（旋转角α满足条件：0°＜α＜90°)，四边形CHGK是旋转过程中两三角板的重叠部分（如图②）.在上述旋转过程中，BH与CH有怎样的数量关系？四边形BHGK的面积有何变化？证明你发现的结论；
在上述旋转过程中，BH＝CK，四边形CHGK的面积不变.
证明：连结CG
∵△ABC为等腰直角三角形，O（G）为其斜边中点
∴CG=BG,CG⊥AB.
∴∠ACG=∠B=45°.
∵∠BGH与∠CGK均为旋转角，
∴∠BGH=∠CGK.
∴△BGH≌△CGK.
∴BH=CK,S△BGH=S△CGK.
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=
S△ABC=××4×4=4.
即：S四边形CHGK的面积为4，是一个定值，在旋转过程中没有变化.
七、(本题12分)
23、用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合.将三角尺绕点A按逆时针方向旋转.
(1)当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时，（如左图），通过观察或测量BE，CF的长度，你能得出什么结论？并证明你的结论；
(2)当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时（如右图），你在(1)中得到的结论还成立吗？简要说明理由.
（1）BE=CF.
证明：在△ABE和△ACF中，
∵∠BAE+∠EAC=∠CAF+∠EAC=60°，
∴∠BAE=∠CAF.
∵AB=AC，∠B=∠ACF=60°，∴△ABE≌△ACF（ASA）.
∴BE=CF.
（2）BE=CF仍然成立.根据三角形全等的判定公理，同样可以证明△ABE和△ACF全等，BE和CF是它们的对应边.所以BE=CF仍然成立.
八、(本题12分)
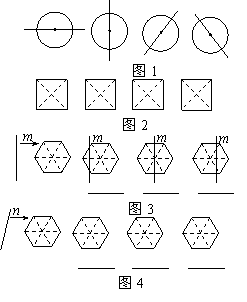24、我们知道：由于圆是中心对称图形，所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).探索下列问题：
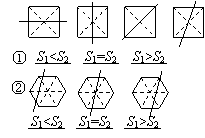
（1）在图2给出的四个正方形中，各画出一
条直线（依次是：水平方向的直线、竖直方
向的直线、与水平方向成45°角的直线和任
意的直线），将每个正方形都分割成面积相等
的两部分；
（2）一条竖直方向的直线m以及任意的直线n，
在由左向右平移的过程中，将正六边形分成左右
两部分，其面积分别记为S1和S2.
①请你在图3中相应图形下方的横线上分别填写
S1与S2的数量关系式(用“<”，“=”，“>”连接)；
②请你在图4中分别画出反映S1与S2三种大小关
系的直线n，并在相应图形下方的横线上分别填
写S1与S2的数量关系式(用“<”，“=”，“>”连接).
（3）是否存在一条直线，将一个任意的平面图形（如图5）分割成面积相等的两部分?请简略说出理由.
 |
（1）
（2）
（3）存在.
对于任意一条直线l ,在直线l从平面图形的一侧向另一侧平移的过程中，当图形被直线l分割后，设直线l两侧图形的面积分别为S1，S2.两侧图形的面积由S1<S2（或S1>S2）的情形，逐渐变为S1>S2（或S1<S2）的情形，在这个平移过程中，一定会存在S1=S2的时刻.因此，一定存在一条直线，将一个任意平面图形分割成面积相等的两部分.