方程(组)与不等式(组)

第二单元　方程(组)与不等式(组)

Ⅰ.考点透视

一、方程与方程组

1、方程、方程组的概念(方程、方程(组)的解，一元一次方程、二元一次方程(组)、一元二次方程及其一般形式，分式方程)

例1.(1)关于x的一元二次方程(a―2)x²+x+a²―4=0的一个解是0，则a=　　　　.

(2)若关于x的方程无解，则m的值是　　　　.

2、方程的解法

(1)整式方程的解法(一元一次方程、二元一次方程(组)、一元二次方程的解法)

例2.(1)用配方法解方程2x²+3x=2　　　　　　 (2)解方程组

(2)可化为一元一次方程的分式方程的解法

例3.解方程

3、方程与方程组的应用

例4.(1)某超市推出如下优惠办法：(1)一次性购物不超过100元不享受优惠；(2)一次性购物超过100元但不超过300元一律九折；(3)一次性购物超过300元一律八折。李明两次购物分别付款80元、252元，如果他是一次性购买与上两次相同的商品，则应付款（　　 ）

A.288元　　 B.332元　　 C.288元或316元　　 D.332元或363元

(2)张老师乘船顺长江而下达到宜昌的姊归茅坪港后，需换乘汽车赶到相距70千米的宜昌三峡机场登机，此时距登机时间还有5小时。经了解汽车由姊归茅坪港驶往宜昌三峡机场的平均速度是50千米/时，途中有三峡工程和西陵峡口等著名的旅游景点，若顺便参观三峡工程需多用2小时，到西陵峡口游玩需再多用1小时。请问张老师游玩这些景点后，会影响赶到山峡机场登机吗？

(3)某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10%，5月份的营业额达到633.6万元，求3月份到5月份营业额的平均月增长率.

二、不等式与不等式组

1、不等式的性质

例5.(1)命题“a、b是实数，若a>b，则a²>b²”若结论保持不变，怎样改变条件，命题才是真命题，以下四种改法：①a、b是实数，若a>b>0，则a²>b²；②a、b是实数，若a>b且a+b>0，则a²>b²；③a、b是实数，若a<b<0，则a²>b²；④a、b是实数，若a<b且a+b<0，则a²>b². 其中真命题的个数是（　　 ）

A．1个　　　　  B．2个　　　　　 C．3个　　　　  D．4个

(2)不等式(a―2)x<2―a的解集是x>―1，则a的取值范围是　　　　.

2、一元一次不等式及其解法

例6.解不等式，并把解集在数轴上表示出来.

3、一元一次不等式组及其解法

例7.求不等式组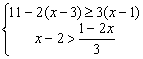的偶数解.

4、一元一次不等式(组)的应用

例7.(1)某校初三年级近期实行小班教学，若每间教室安排20名学生，则少3间教室；若5教室安排24名学生，则空出一间教室，这个学校共有教室多少间？初三年级共有学生多少人？

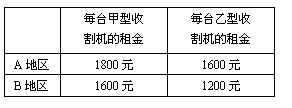(2)光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台。现将这50台联合收割机中的30台派往A地区收割小麦，另20台派往B地区收割小麦。两地区与该农机租赁公司商定的每天的租赁价格如右表：

(1)若农机租赁公司一天获得的租金总额不低于79600元，说明有多少种分配方案，并将各种方案设计出来.

(2)如果要使这50台联合收割机每天获得的租金最高，请你为光华租赁公司提出一条合理建议.

Ⅱ.中考演练

一、选择题(每小题4分，共40分)

1、方程(x+1)²=9的解是（　　 ）

A.x=2　　 B.x=―4　　 C.x₁=2，x₂=―4　　 D.x₁=―2，x₂=4

2、用配方法解一元二次方程x²+8x+7=0，则方程可变形为（　　 ）

A.(x―4)²=9　　 B.(x+4)²=9　　 C.(x―8)²=16　　 D.(x+8)²=57

3、如果分式方程在实数范围内无解，那么m的值为（　　 ）

A.m=1　　 B.m=0　　 C.m=―1　　 D.m≠―2

4、已知方程组的解是，则(a+b)(a―b)的值是（　　 ）

A.―　　 B.　　 C.―16　　 D.16

5、不等式2(x―1)≤x―2的非负整数解的个数是（　　 ）

A.1　　 B.2　　 C.3　　 D.4

6、如果关于x的不等式组无解，那么m的取值范围是（　　 ）

A.m<2　　 B.m≤2　　 C.m>2　　 D.m≥2

7、若方程组的解x和y满足0<x+y<1，则k的取值范围是（　　 ）

A.―4<k<0　　 B.―1<k<0　　 C.0<k<8　　 D.k>4

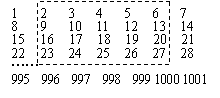
8、将连续的自然数1~1001按如右图所示的方式排列成一个长方形阵列，用一个正方形框出16个数，则这个正方形框出的16个数之和可能等于（　　 ）

A.2000　　 B.2005　 　C.2008　　 D.2080

9、小颖要在一幅长90厘米、宽40厘米的风景画的四周外围，镶上一条宽度相同的金色纸边，制成一幅挂画(如图)，使风景画的面积是整个挂图的54%。设金色纸边的宽为x厘米，根据题意所列方程为（　　 ）

A.(90+x)(40+x)×54%=90×40　　　B.(90+2x)(40+2x)×54%=90×40

C.(90+x)(40+2x)×54%=90×40　　 D.(90+2x)(40+x)×54%=90×40

10、一商家进了一批商品，进价为每件800元，如果要保持销售利润不低于15%，则售价不低于（　　 ）

A.900元　　 B.920元　　 C.960元　　 D.980元

二、填空题(每小题4分，共40分)

11、如果关于x的不等式(a―1)x<a+5和2x<4的解集相同，则a的值为　　　　.

12、若不等式组的解集为―1<x<1，那么(a+1)(b―1)的值为　　　　.

13、若方程组的解为，且k<3，则a―b的取值范围是　　　　  .

14、某书城开展学生优惠售书活动，凡一次性购书不超过200元的一律九折优惠，超过200元的，其中200元按九折算，超过200元的部分按八折酸。某学生第一次去购书付款72元，第二次又去享受了八折优惠，他查看了所买书的定价，发现两次共节省了34元，则该学生第二次购书实际付款　　　　元.

15、有10名菜农，每人可种甲种蔬菜3亩或乙种蔬菜2亩。已知甲种蔬菜每亩可收入0.5万元，乙种蔬菜每亩可收入0.8万元，若要使总收入不低于15.6万元，则最多只能安排　

　　　　人种甲种蔬菜.

三、(每小题8分，共16分)

16、解方程

17、解不等式组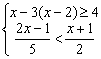，并把解集在数轴上表示出来.

四、(每小题9分，共18分)

18、若a―b+1与互为相反数，求(a―b)²⁰⁰⁵的值.

19、已知不等式组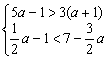的整数解a满足方程组，求代数式(ax―y)(x―ay)的值.

五、(每小题10分，共20分)

20、足球比赛的记分规则是：胜一场得3分，平一场得1分，输一场得0分。一支足球队在某个赛季中共需比赛14场，现已比赛了8场，输了1场，得17分.请问：

(1)前8场比赛中，这之球队共胜了多少场？

(2)这支球队打满了14场比赛，最高得多少分？

(3)通过对比赛情况的分析，这支球队打满14场比赛，得分不低于29分，就可以达到预期的目标，请你分析一下，在后面的6场比赛中，这支球队至少要胜几场，才能达到预期的目标？

21、华联超市用50000元从外地采购回一批“T恤衫”，由于销路好，商场又紧急调拨18.6万元购回比上一次多2倍的“T恤衫”，但第二次比第一次进价每件贵12元，商场在出售时统一按每件80元的标价出售，为了缩短库存时间，最后400件按6.5折处理并很快售完，求商场在这笔生意上盈利多少元？

六、(本题满分12分)

22、某零件制造车间有工人20名，已知每名工人每天可制造甲种零件6个或乙种零件6个，且每制造一个甲种零件可获利润150元，每制造一个乙种零件可获利润260元。如果车间每天所获利润不低于24000元，你认为在这20名工人中，至少要派多少人去制造乙种零件才合适？(其余工人制造甲种零件)

七、(本题满分12分)

23、某商场销售某种品牌的牛奶，已知进价为每箱40元，生产厂家要求每箱售价在40元~70元之间。市场调查发现：若每箱以50元销售，平均每天可销售90箱，价格每降低1元，平均每天多销售3箱，价格每上升1元，平均每天少销售3箱.如果商场平均每天获得900元的利润，那么每箱牛奶应定价多少元？并求平均每天的销售量.

八、(本题满分12分)

24、某生产“科学计算器”公司有100名职工，该公司生产的计算器有百货公司代理销售。经公司多方考察，发现公司的生产能力受到限制，决定引入一条新的计算器生产线生产计算器，并从这100名职工中选派一部分人到新的生产线工作。分工后，继续在原生产线从事计算器生产的职工人均年产值可增加20%，而分派到新生产线的职工人均年产值为分工前人均年产值的4倍。如果要保证公司分工后，原生产线生产计算器的年总产值不少于分工前公司的年总产值，而新生产线生产计算器的年总产值不少于分工前公司生产计算器的年总产值的一半.

(1)试确定分派到新生产线的人数.

(2)当多少人参加新生产线生产时，公司年总产值最大？相比分工前，公司年总产值的增长率是多少？