广东省数学中考摸拟试题

数学中考摸拟试题（1）

 

一、选择题（3×5=15分）

1、下列二次根式中与是同类二次根式的是（　　）

A、　　  B、　　  C、　　  D、

2、下列命题中真命题是（　　）

A、圆柱的侧面展开图是扇形　　　　　  B、三角形的内心一定在三角形内部

C、两个等腰三角形是相似三角形　　　　D、四边形的对角互补

3、点P（2，3）关于x轴对称的点的坐标是　　　。

A 、（2，3）　　　 B、（－2，3）　　　　　 C、（2，－3）　　　　D、（－2，－3）

4、关于x的一元二次方程（a－1）x²＋x+a²－l=0的一个根是0.则a的值为(　)

　 A、　1　　 B、 －l　 　　 C、　1 或－1　 　 D、　

5、在ΔABC中，∠A=30º，∠B=60º，AC=6，则ΔABC的外接圆的半径为（　 ）

A、 2　　 B、 3　　  C、　　　 D、 3

二、填空题（4×5=20分）

6、计算：　　　　  。

7、函数＋中，自变量x的取值范围是　　　　。

8、当k 　　　 时，方程没有实数根。

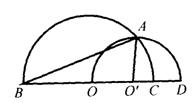
9、如图，点B，O，O^/，C，D在一条直线上，BC是半圆O的直径，OD是半圆O^/的直径，两半圆相交于点A，连结AB，AO^/，若∠BAO^/=81°，则∠AO^/C＝　　　　度。

10、在△ABC中，∠C＝90⁰，如果tanA＝，那么sinB的值等于　　　　　　 。

三、解答下列各题（6×5=30分）

11、计算：

12、计算：

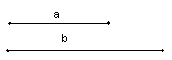
13、已知线段a、b如图：

求作Rt△ABC，使斜边AB＝b，直角边AC＝a。

（不写作法，保留作图的痕迹）

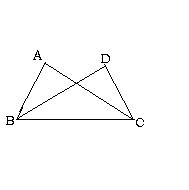
14、已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB有平分线。

求证：AB=DC

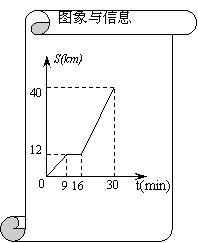
15、如图是某汽车行驶的路程S(km)与时间t(min)

的函数关系图.观察图中所提供的信息，解答下列问题：

（1）汽车在前9分钟内的平均速度是多少？

（2）汽车在中途停了多长时间？

（3）当16≤t≤30时，求S与t的函数关系式

四、（7×4=28分）

16、解不等式，并把解集在数轴上表示出来。

17、解方程：

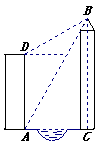
18、如图，小丽的家住在电梯公寓AD内，她家的河对岸新建了一座大厦BC。为了测得大厦的高度，小丽在她家的楼底A处测得大厦顶部B的仰角为60º，爬上楼顶D处测得大厦的顶部B的仰角为30º。已知小丽所住的电梯公寓AD高82米，请你帮助小丽计算出大厦高度BC及大厦与小丽所住电梯公寓间的距离AC。

19、已知：反比例函数y= 的图象与直线y=2x都经过（a，1），抛物线y=kx²+bx+c经过直线y=－3x+3与x轴、y轴的交点，试判断点（a，k）是否在这条抛物线上，并说明理由。

五、（9×3=27分）

20、 如图，(1)是某城市三月份1至10日的最低气温随时间变化的图象。

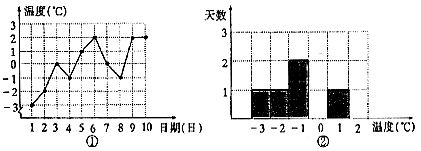
　　（1）根据图(1)提供的信息，在图(2)中补全直方图；

　　（2）这10天最低气温的众数是_______℃，最低气温的中位数是_______℃，最低气温的平均数是_______℃。

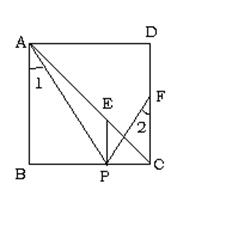21、已知：如图，在正方形ABCD中，F是CD边上的中点，点P在BC上，∠1=∠2，PE⊥BC交AC于点E，垂足为P。求证：AB=3PE。

22、如图，在矩形ABCD中，AB=10cm，BC=20cm.P、Q两点同时从A点出发，分别以1cm/秒和2cm/秒的速度沿A—B—C—D—A运动，当Q点回到A点时，P、Q两点即停止运动，设点P、Q运动时间为t秒。

（1）　　　　　 当P、Q分别在AB边和BC边上运动时，设以P、B、Q为顶点的三角形面积为s，请写出s关于t的函数解析式及自变量t的取值范围。

（2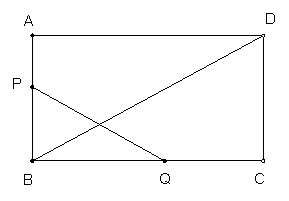）　　　 在整个运动过程中，t取何值时，PQ与BD垂直。　

　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　 

数学中考摸拟试题（2）

一、选择题：（每小题3分,共15分）

1．若(2a+3b)²=(2a－3b)²+(　 )成立，则括号内的式子是(　　　　)。

A. 6ab　　　 B. 24ab　　　 C. 12ab　　　 D. 18ab

2. 如果关于 x 的方程 x+2x-k＝0 没有实数根，那么 k 的取值范围是(　　 )

　　Ａ.k≥-1　　　 Ｂ.k≤1　　　　 Ｃ.k＞1　　　　　 Ｄ.k＜-1

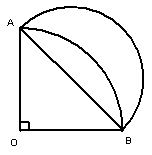3．如图：扇形OAB中，，弦AB=，

以AB为直径作半圆和AB 围成图形面积为（　　 ）

A．　　B．　　 C．　　 D．　　

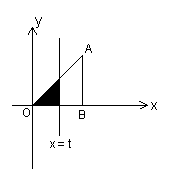4．如右图，直角三角形AOB中，AB⊥OB于B，且

AB = OB =3，设直线截此三角形所得的阴影

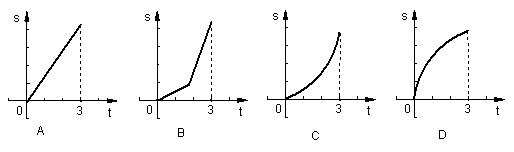
部分的面积为S，则S与的函数关系的图象大致为

（　　 ）

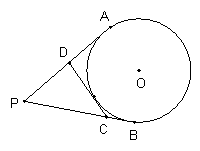5．如图：PA、PB、CD都是⊙O的切线，∠P=60⁰，设△PCD周长为C₁，⊙O的周长为C₂，则C₂与2 C₁的大小关系（　　  ）

A. 　　　B. 　

C.  　　 D. 与⊙O的半径有关

二、填空题：（每题4分，共20分）　　　　　　　　　　　

6. 我国最长的河流长江全长约6300千米，用科学记数法表示为

　　　　　 千米.

7. 梯形的上底长4cm，中位线长7cm, 则下底长　　　cm.

8．当　　　　 时，方程必有两个相等实数根.

9．某出租车公司在“国庆”长假平均每天的营业额为6万元，由此推断10月份的总营业额约为（万元），根据所学的统计知识，你认为这样的推断是否合理？　　　

答：　　　　（答案选“合理”或“不合理”填写）.

10．已知半径为2的⊙A和半径为3的⊙B相外切，又⊙O的圆心在线段AB上，且⊙O与⊙A、⊙B都相交，则⊙O的半径的取值范围是　　　　 .

三、（每小题6分，共30分）

11．计算

12. 若，求的值。

13.  已知直线l和l外的一点P。

求作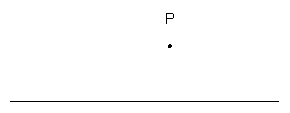：（1）⊙P，使⊙P与直线l相切于A点。

（2）作⊙P的内接△ABC，使由直线l、△ABC和⊙P组成的图形是轴对称图形。　　

L

14．解分式方程：

15. 某人带了100元人民币先到商场买了一些饮料，用去60元。后来，他又买了4千克香蕉，每千克3元，再买了5千克苹果，付钱后尚有节余。如果他买6千克香蕉和6千克苹果，则所带款就不够用了。求苹果的价格范围。

四、（每题7分，共28分）　　　　 　 

16．如图：某地区建设高速公路，在施工段上沿AC方向开山修路，为加快施工进度，要在山坡的另一边同时施工，如图所示，从AC上的一点B取

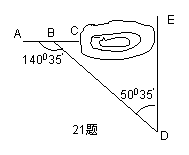∠ABD=，BD=380米，∠D=，那么开挖点E距离D多远，正好使A、C、E成一直线？（精确到0.1米）

17. 已知关于未知数x的方程，

（1）求使原方程有实数根的m的取值范围.

（2）试写出一个m值，使原方程两根中一个大于2，一个小于2，并解这个方程。

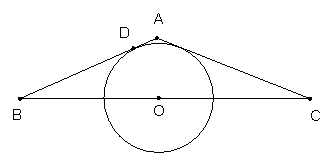18.已知：如图，△ABC为等腰三角形，O是底边BC的中点，⊙O与腰AB相切于点D．

求证：AC与⊙O相切．

 

19.某校准备在甲、乙两家公司为毕业班学生制作一批纪念册，甲公司提出：每册收材料费5元，另收设计费1500元；乙公司提出：每册收材料费8元，不收设计费。

　　（1）请写出制作纪念册的册数x与甲公司的收费（元）的函数关系式。

　　（2）请写出制作纪念册的册数x与乙公司的收费（元）的函数关系式。

　　（3）如果学校派你去甲、乙两家公司订做纪念册，你会选择哪家公司？

五.（每小题9分，共27分）

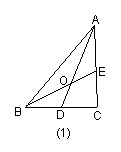
20. 在ΔABC中，D为BC的中点，E为AC上的任意一点,BE交AD于点O．

某学生在研究这一问题时，发现了如下事实：

如图1，当时，有；

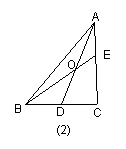
如图2，当时，有；

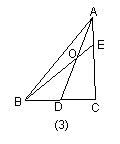
如图3，当时，有；

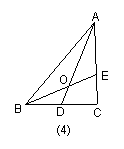
在图4中，当时，参照上述研究的结论，请你猜想用n表示

的一般结论，并给出证明．

21. 张明、王成两位同学10次数学单元自我检测的成绩（成绩均为整数，且个位数为0）分别如下图所示：

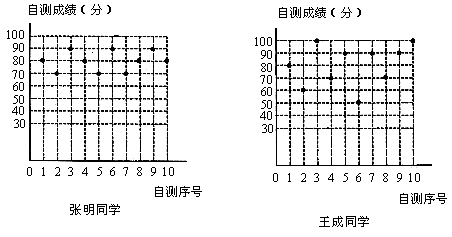
　　利用图中提供的信息，解答下列问题。

　　（1）完成下表：

姓名	平均成绩	中位数	众数	方差（）
张明		80	80
王成				260

　　（2）如果将90分以上（含90分）的成绩视为优秀，则优秀率高的同学是___　　　____；

　　（3）根据图表信息，请你对这两位同学各提一条不超过20个字的学习建议。

22.如图:在⊙O的内接△ABC中, AB+AC=12, AD⊥BC于D，（点D不与点B、C重合），且AD=3，设⊙O的半径为，AB长是，

（1）求与之间的函数关系式，并写出自变量的取值范围。

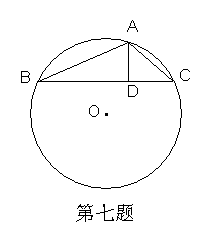（2）当点D为BC的中点时，求⊙O的半径。

广东省数学中考摸拟试题（3）

一、选择题（本题共15分，每小题3分〕

1．已知a、b两个实数互为相反数，那么a、b不满足的关系是　　　（　　）

（A）　（B）（C）　（D）

2．某商品的价格为m元，降价10％后，又降价10％，销量猛增，商店决定再提价20％，提价后该商品的价格为　　　（　　 ）

（A）m元　　（B）0. 97m元　 （C）0.96m元  （D）0.972m元

3．如图，在直角梯形ABCD中，AB=7，AD=2，BC=3，如果边AB上的点P，使得△PAD与△PBC相似，那么这样的点P有　　 （　　）

（A） 1个　（B）2个 （C）3个（ D）  4个

4、一个圆的内接正三角形与内接正六边形的面积比为（　　　）

　　　 A．1∶　　　　　 B．∶　　　　　　　C．1∶2　　　　D．1∶

5．设二次函数，当时，有，则m、n的值是（　　  ）

（A）　　 （B）　（C）一2　　 （D）m＝1，n＝4

二、填空题（本题共20分，每小题4分）

6．–8的立方根与的平方根的和为__________.

7．已知最简根式与是同类根式，则=__________.

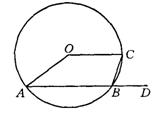
8．如图⊙O的半径为4cm，OC∥AB，D为弦AB延长线上一点，若∠CBD=75⁰，则∠A=__________度，四边形OABC面积为 __________ 。

9．一个菱形ABCD的两条对角线BD=1cm，AC=2cm，那么，菱形的周长为_________，sin∠BAD=________。

10．观察下列等式：

　　 　　　　 

这些等式反映出自然数间的某种规律，设n表示自然数，试用关于n的等式表示出你所发现的规律______________________________。

三、（本题共30分，每小题6分）

11．计算：　　　　　　  12．解方程：

13．解不等式组 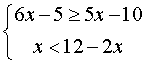 ，　 并把解集在数轴上表示出来。

14．如图，某公路路基横断面为等腰梯形.按工程设计要求路面宽度为10米，坡角为60°，路基高度为12米，求路基下底宽（精确到0.1米）.

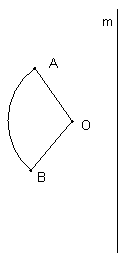
15．作出图中扇形AOB关于直线m的

轴对称图形（保留作图的痕迹）

四、（本题共28分，每小题7分）

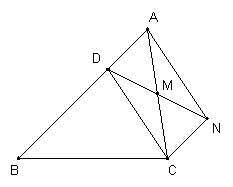
16．已知：D是△ABC的边AB上一点，CN∥AB，DN交AC于M，若MA=MC。　　求证：CD=AN.

17．已知一次函数的图象分别与x、y轴交于A（m，0）、B（0，n）两点，且。当m、n是方程的两根时，求一次函数的解析式。

18、某班学生争取到制作240面彩旗的任务，有10名学生因故没能参加制作，因此这班的其余学生人均要比原计划多做4面彩旗才能完成任务，问这个班有多少名学生？

19、甲、乙两班举行电脑汉字输入速度比赛，各选10名学生参加。各班参赛每分钟输入汉字个数统计如下表：

输入汉字（个）	132	133	134	135	136	137	众数	中位数	平均数（　 ）	方差（ S2 ）
甲班学生（人）	1	0	1	5	2	1	135	135	135	1.6
乙班学生（人）	0	1	4	1	2	2

请你填写上表中乙班的相关数据，再根据所学的统计学知识，从不同方面评价甲、乙两班学生的比赛成绩（至少从两方面进行评价）.

五、（每小题9分，共27分）

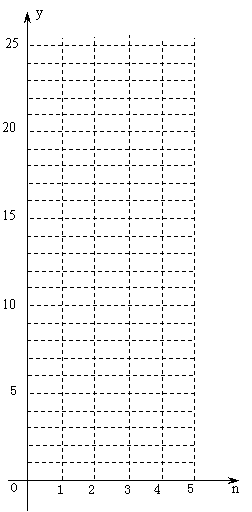
20、同学们都做过《代数》课本第三册第87页第4题：某礼堂共有25排座位，第一排有20个座位，后面每一排都比前一排多1个座位，写出每排的座位数m与这排的排数n的函数关系式并写出自变量n的取值范围。

　　答案是：每排的座位数m与这排的排数n的函数关系式是；自变量n的取值范围是，且n是正整数。

　　

上题中，在其他条件不变的情况下，请探究下列问题：

　　（1）当后面每一排都比前一排多2个座位时，则每排的座位数m与这排的排数n的函数关系式是___________________（，且n是正整数）

（2）当后面每一排都比前一排多3个座位、4个座位时，则每排的座位数m与这排的排数n的函数关系式分别是　　　　　　　　　　　　　 ，

 　　　　　　　　　　　　　　 。（，且n是正整数）。

　　

（3）某礼堂共有p排座位，第一排有a个座位，后面每排都比前一排多b个座位，试求出每排的座位数m与这排的排数n的函数关系式，并指出自变量n的取值范围。

　

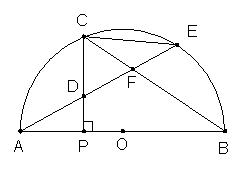21、 已知：如图，C为半圆上一点， = ，过点C作直径AB的垂线CP，P为垂足，弦AE分别交PC，CB于点D，F。

　　（1）求证：；

（2）若，求PB的长。

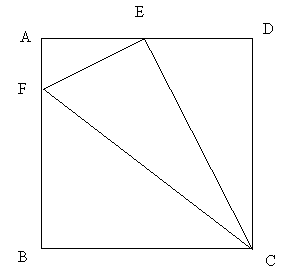
22、如图在矩形ABCD中，E为AD的中点，F为AB上一点，连结FC、EC、EF。

（１）　 若EF⊥EC于E，求证：ΔAEF∽ΔECF；

（２）　 若BC＝2，CD＝3，F为AB上一动点，设AF＝x，S_ΔEFC＝y，求y关于x 的函数关系式，并写出x的取值范围；

（３）　 在（2）的条件下，求当F运动到什么位置时，ΔCEF为等腰三角形。

广东省数学中考摸拟试题（4）

 

一、选择题：（每小题3分，共15分）

1、我国首次载人航天飞船“神州五号”成功绕地球飞行14圈，行程约591000千米，用科学记数法表示正确的是（　　　）

　　A. 　　 B. 　　C. 千米　　　　　 D. 千米

2、右图是某市4月份某一天的温度随时间变化的图象，通过观察可知，下列说法错误的是（　　　 ）

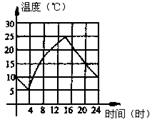
　　A. 这天14时温度最高

　　B. 这天4时温度最低

　　C. 这天最高温度与最低温度的差是21℃

　　D. 这天20时温度为15°

3、用换元法解时，若设，则方程化为（　　）

（A） （B） （C） （D）

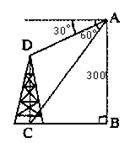
4、 如图，在300m高的峭壁上测得一塔的塔顶与塔基的俯角分别为

30°和60°，则塔高CD为（　　　）

　　A. 200米　　　　　　　　　　　　　　B. 180米

　　C. 150米　　　　　　　　　　　　　　D. 100米

5、 已知线段AB的长为8cm，点A、B到直线m的距离分别是5cm和3cm，这样的直线m共有（　　　　）

　　A. 2条　　　　　　　　　B. 3条　　　　　　　　　C. 4条　　　　　　　　　D. 5条

 二、填空题（每小题4分，共20分）

6、 分解因式　＝　　　　　 。

7、 四边形ABCD是圆内接四边形，若∠A：∠B：∠C=1：2：3，则∠D等于　　　　　　　　  度。

8、 点P（1，－2）关于x轴对称的点在双曲线上，则k的值为　　　　　　　　  。

9、二次函数的顶点坐标是___________________。

10、已知圆锥的母线长为 5cm，底面半径为 3cm，那么圆锥侧面展开图中，

　  扇形的圆心角是　　　　　　  。

 三、解答下列各题：（每小题6分，共30分）

 11、 计算：│－3│－＋(tan21°)⁰-（- ）^－3　

 12、已知的值。

13、 设，求实数x、y的值。

14、作出图中圆的内接正方形（保留作图的痕迹，不要求写作法）

15、体育加试前，张勇为提高长跑速度，每天晚上用匀速跑步1000米。有一天，他跑了2分钟后，速度加快，每分钟比原来多跑了100米，结果比原来少用了1分钟。那么他原来每分钟跑多少米？

　

四、（每小题7分，共28分）

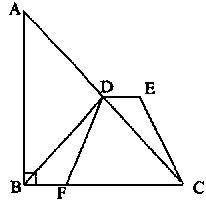16、如图，在Rt△ABC中，BD是斜边AC的中线，DE∥BF且DE=BF。试判断DF与EC的数量关系，并证明你的结论。

 

17、王先生还有8年退休，由于单位离家比较远，需要买车或租车。目前租车市场某型号小汽车月租费为0.24万元；如果购置一辆同样型号的小汽车需要12万元，另加保险费和每年0.4万元。除第一年汽车免费维修外，从第二年起平均每年维修费用为0.22万元。

　　（1）写出租车费用y₁和买车费用y₂与年数x的函数关系式；

（2）若从第4年起租车费下调至每月0.15万元，而汽车的维修费每年比上一年增加0.03万元，请你帮王先生计算一下，这8年是租车合算还是买车合算？

18、如图⑴、⑵、…、(m)是边长均大于2的三角形、四边形、…、凸n边形。分别以它们的各顶点为圆心，以1为半径画弧与两邻边相交，得到3条弧、4条弧……、n条弧。

①图⑴中3条弧的弧长的和为_________________，

图⑵中4条弧的弧长的和为__________________；

②求图(m)中n条弧的弧长的和 (用n表示)。

 

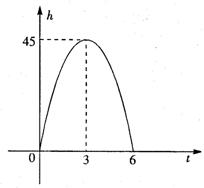
19、对于上抛物体，在不计空气阻力的情况下，有如下关系式：，其中h（米）是上抛物体上升的高度，（米／秒）是上抛物体的初速度，g（）是重力加速度，t（秒）是物体抛出后所经过的时间，如图是h与t的函数关系图．

（1）求：h与t的函数关系式

（2）几秒后，物体在离抛出点25米高的地方？

五、（每小题9分，共27分）

20、甲、乙两人在相同条件下各射靶10次，每次射靶的成绩情况如图所示.

　　

（1）请填写下表：

	平均数	方差	中位数	命中9环以上次数（含9环）
甲	7	5.4		3
乙		1.2

（2）请从下列四个不同的角度对这次测试结果进行分析.　　　　　　　　　　　　　　　　　　　　　　　 

① 从平均数和方差相结合看：

②从平均数和中位数相结合看：

③从平均数和命中9环以上（含9环）的次数相结合看：

④从图象上看两人射击命中环数的走势（分析谁更有潜力）：

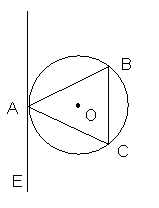21、如图已知△ABC内接于⊙O，AE切⊙O于点A，BC∥AE。

（1）求证：△ABC是等腰三角形；

（2）设，，点P是射线AE上的点，若以A、P、C为顶点的三角形与△ABC相似，问这样的点有几个？并求AP的长；

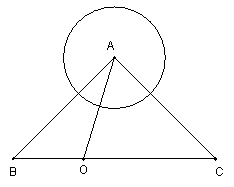
22、在△ABC中, ∠BAC=90°，AB=AC=2，⊙A的半径为1，如图所示，若点O在BC边上运动(与点B、C不重合)，设BO=x，△AOC的面积为y。

(1)　　求y关于x的函数解析式，并写出自变量x的取值范围；

(2)　　以点O为圆心，BO长为半径作圆O，求当⊙O与圆A相切时△AOC的面积。

广东省数学中考摸拟试题（5）

一、 选择题：（每小题3分，共15分）

1、 在函数中，自变量x的取值范围是（　　）

　  A. 　　　　　　　　B.

　  C. 　　　　　　　　　 D.

2、 下列各式计算正确的是（　　）

　  A. 　　　B.

C. 　　　D.

3、 在，若，则（　　）

　  A. 　　　　　　　　 B. 　　　　　C. 　　　　　　　　　　　　D.

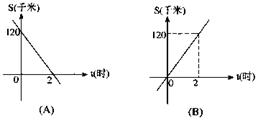4、 汽车由甲地驶往相距120千米的乙地，如果汽车的平均速度是60千米/时，那么汽车距乙地的路程S（千米）与行驶时间t（时）的函数关系用图象表示为（　　）

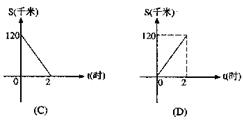
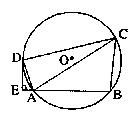
5、 如图所示，四边形ABCD内接于圆O，切线，交BA延长线于点E，若，则的度数为（　　）

　  A. 20°　　　　　　　　　　 B. 40° 　　C. 50°　　　　　　　　　　　　　　D. 70°

二、填空题：（每小题4分，共20分）

6、 在P（-2，-3）关于x轴对称的点Q的坐标为　　　　　　　　  。

7、 因式分解=　　　 　　　　　　　　　 。

8、 不等式组的整数解是________________________。

9、如图所示，边长为2的等边△ABC中，以顶点A为圆心，以高AD长为半径画弧，分别交AB于点E，交AC于点F，则的长为　　　　　　　　　  。

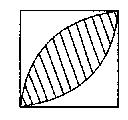
10、 已知正方形的边长为1，分别以两个对角的顶点为圆心，　1为半径画弧，则图中阴影部分的面积是　　　　　　　  。

 

 三. 解答题：（每小题6分，共30分）

11、 计算－（－）^－2

12、化简

13、用换元法解方程

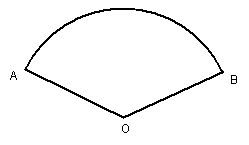14、作图题：请你在图中将扇形AOB的面积分成四等分（不写作法，保留作图的痕迹）

15、列方程（组）解应用题：

　  某书商用800元购进一批图书，并以每套58元的价格全部售完。由于此书畅销，该书商又用1760元再次以比第一次进价每套多4元的价格购进此种图书，数量是第一次进书数量的2倍，仍以每套58元的价格出售。卖了部分书后，为了加快资金周转，书商将剩余的15套书以售价的八五折全部售出。

　  问：（1）该书商第一次购买了此种图书多少套？

　 　　 （2）两次售书共盈利多少元？

 四、（每小题7分，共28分）

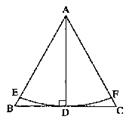
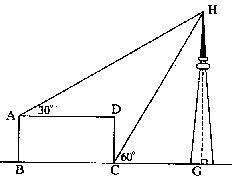　 16、 如图所示，形状为长方形的建筑物ABCD的底端BC的长是70米，高AB=30米，从A、C两点可测得河对面一电视发射塔的顶端H的仰角分别为30°和60°，求塔的高度HG（精确到1米，）

 

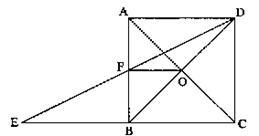17、已知：如图所示，在正方形ABCD中，AC、BD交于点O，延长CB到点E，使BE=BC，连结DE交AB于点F。

　  求证：。

18、 已知：关于x的一元二次方程。

　  （1）求证：不论m为何值，方程总有两个不相等的实数根；

（2）若方程的两个实数根为和，且满足

，求m的值。

　

19、　某工厂生产某种产品，每件产品的出厂价为1万元，其原材料成本价（含设备损耗等）为0.55万元，同时在生产过程中平均每生产一件产品有1吨的废渣产生，为达到国家环保要求，需要对废渣进行脱硫、脱氮等处理，现有两种方案可供选择：

　　方案一：由工厂对废渣直接进行处理，每处理1吨废渣所用的原料费为0.05万元，并且每月设备维护及损耗费为20万元。

　　方案二：工厂将废渣集中到废渣处理厂统一处理，每处理1吨废渣需付0.1万元的处理费。 问：

　　（1）设工厂每月生产x件产品，每月利润为y万元，分别求出方案一和方案二处理废渣时，y与x之间的函数关系式。（利润＝总收入－总支出）

（2）若你作为工厂负责人，如何根据月生产量选择处理方案？

五、（每题9分，共27分）

20、某中学举行了一次知识竞赛，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成的频率分布表和频率分布直方图，解答下列问题：

（1）填充频率分布表中的空格；　　

（2）补全频率分布直方图；

（3）在该问题中的样本容量是多少？ 答：　　　　　　　　　　　　　．

（4）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由）

　　答：　　　　　　　　　　　　　．

（5）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？

　　答：　　　　　　　　　　　　　．

频率分布表
分组	频数	频率
50.5～60.5	4	0.08
60.5～70.5		0.16
70.5～80.5	10	0.20
80.5～90.5	16
90.5～100.5
合计

频率分布直方图

21、如图⊙O是△ABC的外接圆，∠ABC＝45°，AD∥OC交BC的延长线于D，AB交OC于E。

（1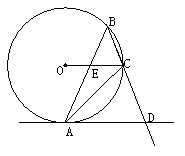）　　　　 求证：AD是⊙O的切线；

（2）　　　　　　　　　　　　　　  若∠ACD＝60°，求BC∶CD的值。

22、观察图1至图5中小黑点的摆放规律，并按照这样的规律继续摆放，记第n个图中小黑点的个数为y。

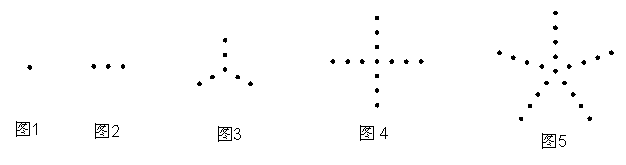
解答下列问题：

⑴ 填表：

n	1	2	3	4	5	…
y	1	3	7	13		…

⑵ 当n＝8时，y＝__________.

⑶ 根据上表中的数据，把n作为横坐标，把y作为纵坐标，在图中的平面直角坐标系中描出相应的各点（n,y），其中1≤n≤5.

⑷ 请你猜一猜上述各点会在某一函数的图象上吗？如果在某一函数的图象上，请求出该函数的解析式.