新课标(北师大版)中考数学第一轮复习测试卷
第六单元 函数
一、选择题(每小题4分，共40分)
1、点P(-1，2)关于y轴对称的点的坐标是（ A ）．
A．（1，2） B．（-1，2） C．（1，-2） D．（-1，-2）
2、已知正比例函数y=kx(k≠0)的图象过第二、四象限，则（ A ）
A.y随x的增大而减小
B.y随x的增大而增大
C.当x<0时，y随x的增大而增大；当x>0时，y随x的增大而减小
D.不论x如何变化，y不变
3、关于函数y= -2x+1，下列结论正确的是（ C ）
A.图象必经过点(﹣2，1) B.图象经过第一、二、三象限
C.当x>
时，y<0
D.y随x的增大而增大
4、一定质量的干松木,当它的体积V＝2m3时,它的密度ρ＝0.5×103kg/m3,
则ρ与V的函数关系式是（ D ）
A. ρ＝1000V B. ρ＝V＋1000 C. ρ＝ D. ρ＝
5、抛物线y=
x2-4x+3的顶点坐标和对称轴分别是( D )
A.(1，2)，x=1 B.(-1，2)，x=-1 C.(-4，-5)，x=-4 D.(4，-5)，x=4
6、将抛物线y=2x2向左平移1个单位，再向上平移3个单位得到的抛物线解析式是( B )
A.y=2(x+1)2+3 B. y=2(x－1)2+3 C. y=2(x+1)2－3 D. y=2(x－1)2-3
7、在直角坐标系中，点P(1，-1)一定在（ D ）
A. 抛物线y=x2上
B. 双曲线y=
上
C. 直线y=x上 D. 直线y=-x上
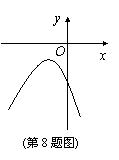
8、二次函数y=ax2+bx+c的图象如图所示，则下列关于a、b、c间的关系判断正确的是（ D ）
A.ab<0 B.bc<0 C.a+b+c>0 D.a-b+c<0
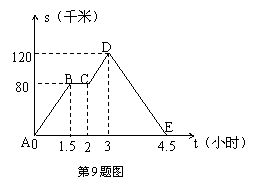9、如图中的图象（折线ABCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为
千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有（ A ）
A、1个 B、2个 C、3个 D、4个
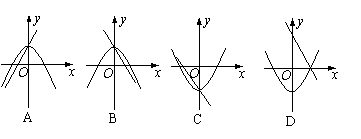
10、在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为（ B ）
 |
二、填空题(每小题4分，共40分)
11、在①y=x；②y= -x；③y=；④y=x+1；⑤y=x2的图象中，是关于原点的中心对称图形的是(填序号) ①②③
.
12、在平面直角坐标系中，直线y=kx+b(k，b为常数，k≠0，b>0)可以看成是将直线y=kx沿y轴向上平行移动b个单位而得到的，那么将直线y=kx沿x轴向右平行移动m个单位（m>0）得到的直线的方程是 y=k(x-m) .
13、若M(-，y1)、N(-
，y2)、P(，y3)三点都在函数
(k<0)的图象上，则y1、y2、y3的大小关系为 y2>y1>y3 .
14、抛物线y=x2-2x-3与x轴分别交于A、B两点，则AB的长为__4______．
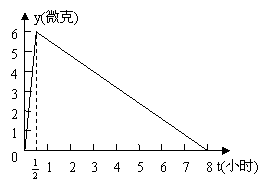
15、某种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y(微克)与时间t(小时)之间的关系如图所示。据测定：每毫升血液中含药量不少于4微克时，治疗疾病有效。假若某病人(成人)某天服药时间是7：00，则此人服药后对治疗疾病有效的时间范围是 7：00~10：00 .
三、(每小题8分，共16分)
16、已知正比例函数y=k1x的图像与一次函数y=k2x-9的图像交于点P(3,－6).
（1）求k1、k2的值；
（2）如果一次函数y=k2x-9的图像与x轴交于点A，求点A的坐标.
（1）把P(3,－6)分别代入两个解析式，得k1= -2，k2=1；（2）A(9,0)
17、已知一次函数y=kx+b的图象与反比例函数y=
的图象交于点A(-2，1)、B(1，n).
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值大于反比例函数的值的x取值范围.
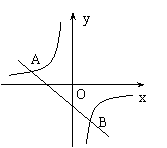（1）y=
，y=-x-1
（2）x<-2或0<x<1.
四、(每小题9分，共18分)
18、在某一电路中，保持电压不变，电流I(安培)与电阻R(欧姆)成反比例，当电阻R=5欧姆时，电流I=2安培。
（1）求I与R之间的函数关系式
（2）当电流I=0.5安培时，求电阻R的值；
(1)I=
(2)20欧姆
19、某公司市场营销部的营销员的个人月收入与该营销员每月的销量成一次函数关系，其图象如图所示. 根据图象提供的信息，解答下列问题：
(1)求出营销人员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式；
(2)已知该公司营销员李平5月份的销售量为1.2万件，求李平5月份的收入.
 |
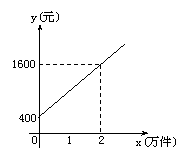(1)依已知条件可设所求的函数关系式为y=kx+b
∵函数图象过(0,400)和(2,1600)两点
∴
解这个方程组，得
∴所求的函数关系式为y=600x+400
(2)当x=1.2时，y=600×1.2+400=1120(元) ，即李平5月份的收入为1120元.
五、(每小题10分，共20分)
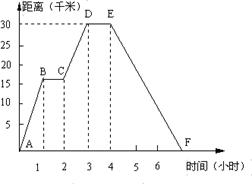
20、小明同学骑自行车去郊外春游，下图表示他离家的距离y（千米）与所用的时间x（小时）之间关系的函数图象.
（1）根据图象回答：小明到达离家最远的地方需几小时？此时离家多远？
（2）求小明出发两个半小时离家多远？
（3）求小明出发多长时间距家12千米？
（1）由图象可知小明到达离家最远的地方需3小时；此时，他离家30千米
（2）设直线CD的解析式为y=k1x+b1,由C（2，15）、D（3，30），代入得：y=15x-15，（2≤x≤3）
当x=2.5时，y=22.5（千米）答：出发两个半小时，小明离家22.5千米.
（3）设过E、F两点的直线解析式为y=k2x+b2，由E（4，30）、F（6，0），代入得y=-15x+90,(4≤x≤6)
过A、B两点的直线解析式为y=k3x，∵B（1，15） ∴y=15x.(0≤x≤1)
分别令y=12，得x=
（小时），x=
（小时）.
答：小明出发小时或小时距家12千米.
22、观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放.记第n个图中小黑点的个数为y.
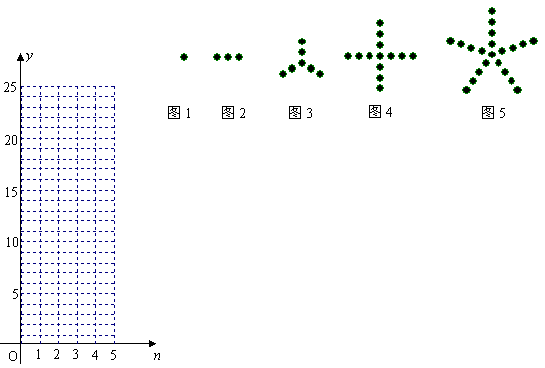
解答下列问题：
（1）填表：
| n | 1 | 2 | 3 | 4 | 5 | … |
| y | 1 | 3 | 7 | 13 | … |
（2）当n＝8时,y＝＿＿＿＿＿＿；
（3）根据上表中的数据,把n作为横坐标,把y作为纵坐标,在左图的平面直角坐标系中描出相应的各点(n, y),其中1≤n≤5；
（4）请你猜一猜上述各点会在某一函数的图象上吗？如果在某一函数的图象上,请写出该函数的解析式.
（1）21 （2）57 （3）(图略) （4）在一个函数的图象上，该函数的解析式为y=n2-n+1
六、(本题12分)
22、“五一”前夕，某旅行社要印刷旅游宣传材料，甲印刷厂提出：每份材料收0.2元印刷费，另收500元制版费；乙印刷厂提出：每份材料收0.4元印刷费，不收制版费.
(1)分别写出两印刷厂的收费y(元)与印刷数量x(份)之间的函数关系式；
(2)在同一坐标系中画出这两个函数的图象；
(3)旅行社要印刷2400份宣传材料，选择哪家印刷厂比较合算？
(4)旅行社拟拿出2000元用于印刷宣传材料，哪家印刷厂印刷的多？多多少份？
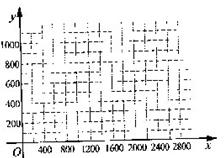
(1)甲厂：y=0.2x+500 乙厂：y=0.4x (2)图略 (3)选择乙厂比较合算 (4)选择甲厂多印刷2500份
七、(本题12分)
23、某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：
| x(元) | 15 | 20 | 30 | … |
| y(件) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数.
（1）求出日销售量y（件）与销售价x(元)的函数关系式；（6分）
（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？（6分）
(1)y=-x+40 (2)产品的销售价应定为25元，此时每日获得最大销售利润为225元
八、(本题12分)
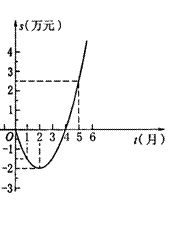
24、为了顺应市场要求，某县花炮厂技术部研制开发一种新产品，年初上市后，公司经历了从亏损到盈利的过程.下面的二次函数图象（部分）刻画了该厂年初以来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s和t之间的关系）.根据图象提供的信息，解答下列问题：
（1）由已知图象上的三点坐标，求累积利润s（万元）与时间t（月）之间的函数关系式；
（2）求截止到几月末花炮厂累积利润可达到30万元？
（3）求第8个月公司所获利润是多少万元？
（1）设二次函数解析式为s=at2+bt+c
∵ 图象经过（0，0），（4，0），（2，-2）
由题意，得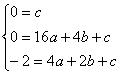
解得
∴ 
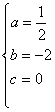
(t ≥0)
（2）当s=30时，
解得t1=-6(不合题意，舍去)，t2=10
∴ 截止到10月末花炮厂累积利润达30万元
（3）当t=8时，s1=
(万元)
当t=7时，s2=
(万元)
∴ 第8个月公司利润为s1- s2=16-10.5=5.5(万元)