第三单元 函数与统计概率
Ⅰ.考点透视
一、函数
1.平面直角坐标系(象限，点的坐标，坐标轴及各象限内点的坐标特征，对称点的特征等)
例1.(1)已知点P（－3，2），点A与点P关于y轴对称，则点A的坐标是_________。
(2)若a<0，则点P(-a2-2，2-a)关于x轴的对称点P′在第 象限.
2.函数及其图象与性质
(1)函数(函数的概念，函数的表示方法—解析式、表格、图象，待定系数法等)
(2)常见的函数的图象与性质(一次函数、正比例函数、反比例函数、二次函数的图象与性质)
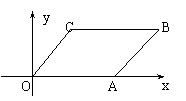
例2.如图，在直角坐标系中，平行四边形OABC的顶点坐标B（17、6），C（5、6），直线y=
恰好将平行四边形OABC的面积分成相等的两部分，求b的值.
例3.已知反比例函数y=
和一次函数y=2x-1的图象在第一象限的交点为A，其中一次函数图象经过(a，b)(a+1，b+k)两点.
(1)求反比例函数的解析式；
(2)在x轴上是否存在点P，使△AOP为等腰三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由.
例4.某公司新进一批商品，每件商品进价2000元，为了解该商品的销售情况，公司统计了该商品一段时间内日销售单价x(千元)和日销售y(件)的数据如下：
| x（千元） | 2.5 | 3 | 3.5 | 4 | 5 |
| y（件） | 20 | 18 | 16 | 14 | 10 |
(1)探究并确定日销售量y(件)与日销售单价x(千元)之间的函数关系式；
(2)设日销售利润L千元(利润＝收入－成本，其他因素不考虑)，写出L与x的函数关系式，并回答：当x为何值时，日销售利润L有最大值？最大值是多少？日销售利润L有最小值吗？如果有，是多少？
二、统计
1.统计的有关概念(总体、个体、样本、样本容量，平均数、众数、中位数，方差、标准差，频数、频率等)
例5.在一次数学知识竞赛中，某班20名学生的成绩如下表所示：
| 成绩(单位：分) | 50 | 60 | 70 | 80 | 90 |
| 人数 | 2 | 3 | 6 | 7 | 2 |
分别求这些学生成绩的中枢、中位数和平均数.
2.统计经历的一般过程(收集数据、整理数据、分析数据、作出决策)
例6.某公司为了评价甲、乙两位营销员去年的营销业绩，统计了这两人去年12个月的营销业绩（所推销商品的件数）分别如下图所示：
甲 乙
(1)利用图中信息，完成下表：
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲 | 7 | |||
| 乙 | 1.5 |
(2)假若你是公司主管，请你根据（1）中图表信息，应用所学的统计知识，对两人的营销业绩作出评价。
Ⅱ.中考演练
一、选择题(每小题4分，共40分)
1、已知A(5，-2)，B(-5，-2)，C(5，2)，则（ ）
A. A、B关于x轴对称 B. A、C关于x轴对称
C. A、B关于原点对称 D. B、C关于y轴对称
2、点P(x+1, x－1)不可能在第（ ）象限
A.一 B.二 C.三 D.四
3、如果一条直线
经过不同的三点A（a，b）、B（b，a）、C(a-b，b-a)，那么直线经过（ ）
A、第一、三象限 B、第一、二、三象限
C、第二、三、四象限 D、第一、三、四象限
4、反比例函数y=k/x的图象经过点P(－4，3)，则k 的值等于( )
A、12 B、－3/4 C、－4/3 D、－12
5、已知反比例函数y=
一次函数y=kx+b的图象的一个交点坐标为(2，-1)，则点(k，b)关于y轴的对称点是（ ）
A.(-2，3) B.(2，-3) C.(2，3) D.(-2，-3)
6、如图，是甲、乙两家商店销售同一种产品的销售价y（元）与销售量x（件）之间的函数图象.下列说法：①售2件时甲、乙两家售价一样；②买1件时买乙家的合算；③买3件时买甲家的合算；④买乙家的1件售价约为3元，其中正确的说法是（ ）
A．①② B．②③④ C．②③ D．①②③
 | |||||
 | |||||
 | |||||
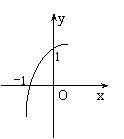(第6题图) (第7题图) (第8题图)
7、如图，矩形OABC的顶点A、C在坐标轴上，顶点B的坐标是（4，2），若直线y=mx-1恰好将矩形分成面积相等的两部分，则m的值为（ ）
A.1 B.
C.
D.2
8、已知函数有y=ax2+bx+c的图象的一部分如图所示，则a+b+c的取值范围是（ ）
A、-2<a+b+c<0 B、-2<a+b+c<2 C、0<a+b+c<2 D、a+b+c<2
9、由小到大的一组数：1，2，ｘ，5，6，7中，这组数的中位数是4，则ｘ为（ ）
A.2 B.3 C.4 D.5
10、数据8，10，12，9，11的平均数和方差分别是（ ）
A.10和
B.10和2 C.50和
D.50和2
二、填空题(每小题4分，共40分)
11、已知反比例函数y=的图象在一、三象限，那么直线y=kx—k不经过第 象限．
12、某超市利用“五、一”开展促销活动，店前公告如下：凡是一次性购买3件某种服装，每件仅售价80元，如超过3件，则其超过部分打8折，顾客所付款y (元)与所购买的件数x（x≥3）之间的函数关系式为 。
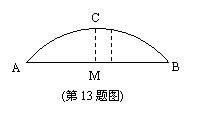
13、如图，一桥拱呈抛物线状，桥的最大高度是16米，跨度
是40米，在线段AB上离中心M处5米的地方，桥的高度是
m (π取3.14).
14、把抛物线y=x2+bx+c的图象向右平移2个单位，再向下平移2个单位，所得图象的解析式为 y=x2-2x+1，则b= ，c= .
15、今年3月甲、乙两种股票连续10天的开盘价格如(单位：元)
| 甲 | 5.23 | 5.28 | 5.35 | 5.3 | 5.28 | 5.2 | 5.08 | 5.31 | 5.44 | 5.46 |
| 乙 | 6.3 | 6.5 | 6.7 | 6.52 | 6.66 | 6.8 | 6.9 | 6.83 | 6.58 | 6.55 |
则在这10天中，甲、乙两种股票波动较大的是 .
三、(每小题8分，共16分)
16、某同学进行社会调查，随机抽查了某个地区的20个家庭的收入情况，并绘制了统计图.请你根据统计图给出的信息回答：
(1)填写完成下表：
| 年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
| 家庭户数 |
(2)这20个家庭的年平均收入为______万元；
(3)样本中的中位数是______万元，众数是______万元；
(4)在平均数、中位数两数中，______更能反映这个地区家庭的年收入水平.
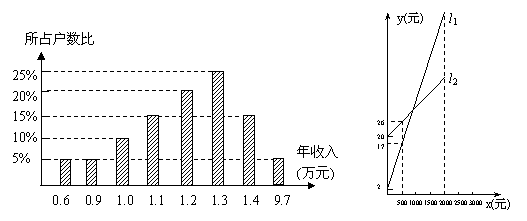
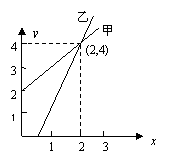
17、如图， l1、l2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费，单位：元)与照明时间x(小时)的函数图象，假设两种灯的使用寿命都是2000小时，照明效果一样.
(1)根据图象分别求出l1、l2的函数关系式；
(2)当照明时间为多少时，两种灯的费用相等？
(3)小亮房间计划照明2500小时，他买了一个白炽灯和一个节能灯，请你帮助他设计最省钱的用灯方法(直接给出答案，不必写出解答过程).
四、(每小题9分，共18分)
18、某广告公司欲招聘过高策划人员一名，对甲、乙 丙三名候选人进行了三项素质测试，他们的各项测试成绩如下表所示：
| 测试项目 | 测试成绩 | ||
| 甲 | 乙 | 丙 | |
| 创新能力 | 72 | 85 | 67 |
| 综合知识 | 50 | 74 | 70 |
| 计算机操作 | 88 | 45 | 67 |
(1)如果根据三项测试的平均成绩确定录用人员，那么谁将被录用？
(2)根据实际需要，公司将创新能力、综合知识、计算机操作三项测试的得分按431的比重确定各人的测试成绩，此时谁将被录用？
19、某校为了表彰部分优秀初三学生，评出一等奖2个、二等奖5个、三等奖10个，并且决定给获奖的学生颁发奖品，同一等次的奖品相同，且只能从下表所列物品中选取一件：
| 品名 | 运动鞋 | 笛子 | 口琴 | 相册 | 书 | 圆规 | 钢笔 | 笔记本 |
| 单价 | 36元 | 24元 | 18元 | 15元 | 12元 | 6元 | 5元 | 4元 |
(1)如果获奖等级越高，奖品单价越高，则学校最多要花多少钱购买奖品？
(2)学校要求一等奖的单价是二等奖的2倍，二等奖的单价是三等奖的3倍，
①如果设三等奖的单价为x元，求出总奖额y元与x的函数关系式？
②如果总奖额不超过230元，则三等奖获得者的奖品有几种可能？
五、(每小题10分，共20分)
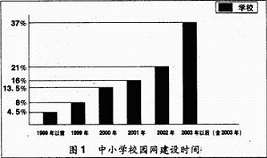
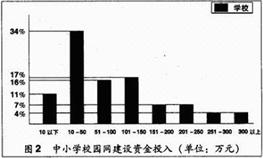
20、据《中国教育报》2004年5月24日报道：目前全国有近3万所中小学建设了校园网。该报为了了解这近3万所中小学校园网的建设情况，从中抽取了4600所学校，对这些学校校园网的建设情况进行问卷调查，并根据答卷绘制了如图的两个统计图。
根据上面的文字和统计图提供的信息回答下列问题：
(1)在这个问题中，总体指什么？样本容量是多少 ？
(2)估计：在全国已建设校园网的中小学中：
①校园网建设时间在2003年以后(含2003年)的学校大约有多少所？
②校园网建设资金投入在200万元以上(不含200万元)的学校大约有多少所？
(3)在所抽取的4600所学校中，校园网建设资金投入的中位数落在哪个资金段内？
图中还提供了其他信息，例如：校园网建设资金投入在10---50万元的中小学数量最多等，请再写出其他两条信息。
21、已知抛物线L：y=ax2+bx+c（其中a、b、c都不等于0），它的顶点是P，与y轴的交点是M。我们称以M为顶点，对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线，直线PM为L的伴随直线.
(1)请直接写出抛物线y=2x2―4x+1的伴随抛物线和伴随直线的解析式：
伴随抛物线的解析式 ，
伴随直线的解析式 ；
(2)若一条抛物线的伴随抛物线和伴随直线分别是y=―x2―3和y=―x―3，则这条抛物线的解析式是 ；
(3)求抛物线L：y=ax2+bx+c（其中a、b、c都不等于0）的伴随抛物线和伴随直线的解析式；
六、(本题满分12分)
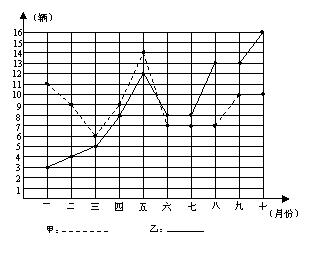22、某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：
（1）请你根据上图填写下表：
| 销售公司 | 平均数 | 方差 | 中位数 | 众数 |
| 甲 | 9 | |||
| 乙 | 9 | 17.0 | 8 |
（2）请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：
①从平均数和方差结合看；
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看（分析哪个汽车销售公司较有潜力）.
七、(本题满分12分)
23、某商店购进一批单价为16元的日用品，为了获得最大的利润，在销售一段时间后，商店对每天的销售情况作了以下统计，随机抽取了一部分，情况如下表所示：
| 每件销售价(元) | 20 | 25 | 35 | 40 | … |
| 每天售出件数 | 360 | 300 | 180 | 120 | … |
假设当天顶的售价是不变的，且每天销售情况均服从这种规律.
(1)观察这些统计数据，找出每天销售件数y与每件售价x(元)之间的函数关系，并写出该函数关系式.
(2)门市部原设有两名营业员，但当销售量较大时，在每天售出量超过168件时，则必须增派一名营业员才能保证营业有序进行，设营业员每人每天工资为40元。求每件产品定价多少元，才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额，其他开支不计).
八、(本题满分12分)
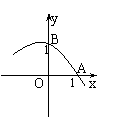24、二次函数y=ax2+bx+c的图象的一部分如右图，已知它的顶点M在第二象限，且经过点A（1，0）和点B（0，1）。
（1）请判断实数a的取值范围，并说明理由；
（2）设此二次函数的图象与
轴的另一个交点为C，当ΔAMC的面积为ΔABC面积的
倍时，求a的值。