九年级上学期期末数学复习试卷
班级 姓名 考号 得分
一、填空题：
1．方程4x2－45＝31x的二次项系数为： ，一次项系数为： ，常数项为： _。
2．已知方程
的一个根是1，则另一个根是 ，
的值是 。
3．一个三角形三边长分别为6cm、8cm、10cm，则这个三角形的面积是 。
4．为美化环境，某社区第一年植树100亩，从第一年到第三年共植树364亩，设连续两年植树面积的平均年增长率为
，则依题意列方程是 ；
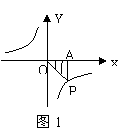5．如图1,P是反比例函数的图象上一点，过P点向x轴作垂线，垂足为A，所得的三角形PAO的面积为3，这个反比例函数的解析是式为
.
6．菱形的两条对角线长为6cm和8cm，则菱形的周长是 ，
面积是 .
7．已知函数
，当x<0时，其图象在第 象限，y随x的增大而 .
8．等腰三角形一腰上的高与另一腰的夹角为30°，则其顶角的度数为 度．
9．在联欢晚会上，有A、B、C三名同学站在一个三角形的三个顶点位置上，他们在玩一个游戏，要求在他们中间放一个木凳，
使他们抢坐到凳子的机会相等，试想想凳子应放在△ABC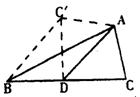
的
的位置最适当．
10．如图2，AD是△ABC的中线，∠ADC＝45°，把△ADC沿AD对折，
点C落在C/的位置，如果BC=2， 则BC′= ．
11．已知函数
（n是常数）当n= 时，此函数是反比例函数。
12．已知y与x2成正比例，且当x=2时，y=16，那么y与x之间的函数关系式是 。
13．.如果一次函数y=kx+b和反比例函数
的图象都经过（-2，1）点，则b的值是
。
14．等腰三角形周长为10 ，腰为x ，底为y时，函数关系式y = ，自变量x的取值范围是 。
15．要使方程（m-2）x2 +x-7=0是一元二次方程，必须
二．选择题
16．已知2x2+x-2的值为3，则4x2+2x+1的值为 ( )
（A）10 （B）11 （C）10或11 （D）3或11
17．一次函数y = - 2x - 3的图象不经过（ ）
A、第一象限 B、 第二象限 C、第三象限 D、第四象限
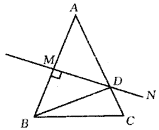
18．已知：如图，AB＝AC，∠Ａ＝36°，AB的垂直平分线交AC于D，
则下列结论：①∠C＝72°；②BD是∠ABC的平分线；
③△ABD是等腰三角形；④△BCD是等腰三角形，其中正确的有（ ）
Ａ．1个 Ｂ．2个 Ｃ．3个 Ｄ．4个
19．一个正方形和一个等腰三角形有相等的周长，已知等腰三角形有两边长分别为5.6ｃｍ和13.2ｃｍ，则这个正方形的面积为（ ）
Ａ．64ｃｍ２ Ｂ．48ｃｍ２ Ｃ．36ｃｍ２ Ｄ．24ｃｍ２
20．如图，两个同心圆中，大圆的半径是小圆半径的2倍，把一粒大米抛到圆形区域中，
则大米落在小圆内的概率为（ ）
A． 
B．
C． 
D．无法确定
21．如果矩形的面积为6cm2，那么它的长
cm与宽cm之间的函数关系用图象表示大致
是（ ）
 |  |  | |||||
 | |||||||
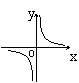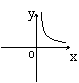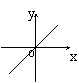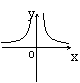A B C D
22．某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标志，然后放回，待有标志的黄羊完全混合于黄羊群后，第二次捕捉40只黄羊，发现其中两只有标志。从而估计该地区有黄羊（ ）
A．200只 B. 400只 C. 800只 D. 1000只
23．用配方法解下列方程时，配方有错误的是 （ ）
A、x2-2x-99=0化为(x-1)2=100 B、x2+8x+9=0化为(x+4)2=25
C、2t2-7t-4=0化为
D、3y2-4y-2=0化为
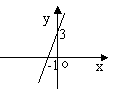24．.如图中，直线的解析式是（ ）
A、y = 3x +3 B、y =3x -3
C、y=-3x +3 D、y = -3x -3
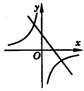
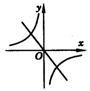
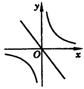
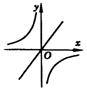25．函数y＝kx和
（k≠0）在同一坐标系中的图象是（ ）
（A） （B） （C） （D）
|
26.如图，正比例函数y=kx（k＞0）与反比例函数
的
（ ）
|
图象相交于A、C两点，过A作x轴的垂线交x轴于B，
|
|
|
A、s
= 1
B、s = 2
|
27．手机的电话号码是由11位数字组成的，一个人的手机号码位于中间的数字为5的机会
为（ ）
A、
B、
C、
D、
28．掷两颗骰子，设出现点数之和为12,11,10的机会依次为
，
，
，成立的是（ ）
(A)=< (B)<= (C)<< (D)
>>
29．掷两颗骰子， “点数和为7”的机会为（ ）
(A)
(B) 
(C)
(D) 
30．在所有的两位数中，任取一个数，该数能被2或3整除的机会是＿＿
(A) 
(B) 
(C) (D) 
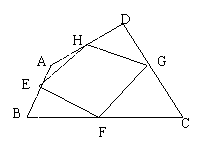３１、如图，E、F、G、H分别是四边形ABCD
四条边的中点，要使四边形EFGH为矩形，
四边形ABCD应具备的条件是（ ）
A、一组对边平行而另一组对边不平行
B、对角线相等
C、对角线互相垂直
D、对角线互相平分
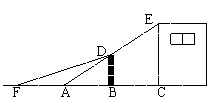３２、如图所示，在房子的屋檐E处安有一台监视器，房子前有一面落地的广告牌（BD），那么监视器的盲区在（
）
A、△ACE B、△BFD
C、四边形BCED D、△ABD
三、解答题
3３．解下列方程：（每小题3分，共6分）
① (2x－1)(x+3)=4 ② x(3x-2)=12x-8
③ ( √2-1)x2
=(√2-1)x
④ 
3４．一个口袋中有8个黑球和若干个白球,(不许将球倒出来数)从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程,如果共摸了200次,其中有60次摸到黑球,那么请你估计口袋中大约有多少个白球?
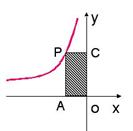3５．如图：P是反比例函数
图象上的一点，由P分别向轴和轴引垂线，阴影部分面积为
，求函数的表达式。
3６．利用树状图求：把一 枚均匀的硬币连续抛掷三次，“至少有一个硬币是正面朝上”
的概率。
3７．作出如下图正三棱柱的三种视图
|
| ||||||
| |||||||
3８．已知：如图，四边形ABCD是平行四边形，P、Q是直线AC上的点，且AP=CQ。
求证：四边形PBQD是平行四边形。
3９．小明和他的同学小颖在阳光下行走，小明身高1.80m，他的影长2.0m，小颖比小明矮0.1m，此刻她的影长是多少？
４０．小明和小亮用如图所示的两个转盘做游戏，转动两个转盘各一次.若两次数字之和为奇数，则小明胜；若和为偶数，则小亮胜.这个游戏对双方公平吗？说说你的理由.
４１．近视眼镜的度数与镜片焦距成反比.小明到眼镜店调查了一些数据如下表：
| 眼镜度数y(度) | 400 | 625 | 800 |
| 镜片焦距x(cm) | 25 | 16 | 12.5 |
（1） 求眼镜度数y(度)与镜片焦距x(cm)之间的函数关系式；
（2） 若小明所戴眼镜度数为500度，求该镜片的焦距.
4２．按要求填图
下面图中，表达了四边形、平行四边形、矩形、菱形、正方形之间的关系。
请你依照“四边形
平行四边形”的填法，在每个括号内填上一个条件（只填一个即可），使得前一种四边形满足这一条件后，成为后一种四边形。
4３．某商店进了一批服装，进货单价为50元，如果按每件60元出售，可销售800件，
如果每件提价1元出售，其销售量就减少20件。现在要获利12000元，且销售成本不超过24000元，问这种服装销售单价确定多少为宜？这时应进多少服装？
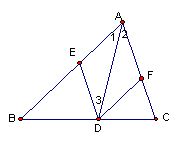4４．已知：如图
中，AD是
的角平分线，DE∥AC，DF∥AB。
求证：四边形AEDF是菱形。
对于这道，小明是这样证明的。
证明：∵AD平分 （已知）
∴∠1＝∠2 （角平分线的定义）
∵DE∥AC （已知）
∴∠2＝∠3 （两直线平行内错角相等）
∴∠1＝∠3 （等量代换）
∴AE＝DE （等角对等边）
同理可证：AF=DF
∴四边形AEDF是菱形（菱形定义）
老师说小明的证明过程有错误，你能看出来吗？
⑴请你帮小明指出他的错误是什么？
⑵请你帮小明做出正确的解答。
４５．已知y=y1+y2 ，y1与x成正比例，y2与x2成反比例，且x=2与x=3时，y的值都等于19，求y与x之间的函数关系式。
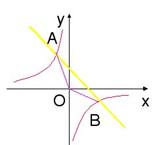
４６．如图，已知一次函数
的图象与反比例函数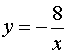
的图象交于A，B两点，且A点的横坐标与B点的纵坐标都是
；
（1） 一次函数的解析式
（2） △AOB的面积。
