华师大九年级数学（上）期终综合练习
一、填空题：（每空2分，共34分）
1. 
＝ ；
＝ .
2. 一种细菌的半径是0.00004m，用科学记数法表示它为 m.
3.. 当m＝ 时，方程
是一元二次方程.
4. 写出一个含有字母
的分式，使得该分式当
时无意义，
当
时其值为０，你写出的分式是 ．
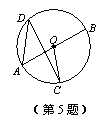
5. 如图，在⊙O中，AB是⊙O的直径，∠D＝40°，则∠BOC的度数为__ _.
6. 若
，
，则
＝ ，
＝ .
7. 为了调查某市今年有多少名考生参加中考，小华从全市所有家庭中随机抽查了200个家
庭，发现其中10个家庭有子女参加中考．已知该市约有1.3×106个家庭，假设有子女参
加中考的每个家庭中只有一名考生，请你估计今年该市约有 名考生参加中考?
8. 一个直角三角形斜边长为
，内切圆半径为
，则这个三角形的周长是 cm.
9. 在△ABC和△ADC中，有下列三个论断：①AB＝AD；②∠BAC＝∠DAC；③BC ＝DC．将
其中两个论断作为条件，另一个论断作为结论构成一个命题，写出一个真命题是：
．
10. 若圆锥的母线长为4cm，底面半径为3cm，则圆锥的侧面展开图的面积是 cm2.
11．已知⊙O1与⊙O2相切，⊙O1的半径是3，O1O2＝5，则⊙O2的半径是 .
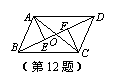
12．如图，□ABCD中，AE⊥BD于E，CF⊥BD于F，则图中共有
对全等三角形.
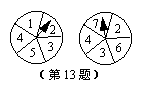13．如图所示的两个圆盘中，指针落在每一个数上的机会均等，
那么两个指针同时落在偶数上的概率是 .
14．如图，⊿ACO中，OA=3cm，OC=1cm，将⊿ACO绕点
O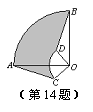
顺时针旋转90º至⊿BDO的位置，则AC边扫过的
图形（阴影部分）的面积是 cm2.
15．在⊿ABC中，∠C＝90º，AC＝3，BC＝4，若以C为圆心，
R为半径的圆与斜边AB只有一个公共点，则R的范围是 .
二、选择题：（每小题2分，共16分）
1. 下列各式计算正确的是（ ）
A．
B．
C．
D．
2. 计算
的结果是( )
A. 
B. 
C. D.
3. 关于的一元二次方程
的一个根是0，则
的值为（ ）
A. 1 B.－1 C. 1或－1 D. 0.5
4．如图，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是
（ ）
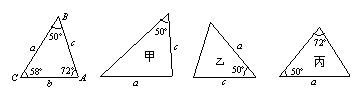A．甲和乙 Ｂ．乙和丙
Ｃ．只有乙 Ｄ．只有丙
5. 为调查某校初三学生周日的睡眠时间，选取调查对象最合适的是（ ）
A. 选取一个班级的学生 B. 选取50名男生
C. 选取50名女生 D. 随机选取50名初三学生
6. 关于的方程
有两个不相等的实数根，则
的取值范围是（ ）
A．
B．
C．
D．
7．已知两圆相交，其圆心距为6，大圆半径为8，则小圆半径
的取值范围是（ ）
A．＞2 B．2＜＜14 C．2＜＜6 D．2＜＜8
8．下列四个命题：①三个点确定一个圆；②垂直于圆的半径的直线是圆的切线；③圆的切线
垂直于经过切点的半径；④三角形的内心到这个三角形的三个顶点的距离相等；⑤在同一
圆内，同弦或等弦所对的圆周角相等．其中正确的命题的个数是（ ）
A．1个 B．2个 C．3个 D．4个
三、计算：（每小题4分，共8分）
1． 2.
化简求值：
，其中
.
四、解方程：（每小题4分，共8分）
1. 
2. 
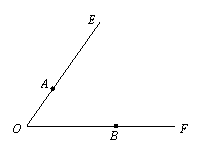
五、（本题满分4分）如图，已知：∠EOF，点A、B分别在OE、OF上．
求作：点P，使点P到∠EOF两边OE、OF的
距离相等，且PA＝PB．
六、（本题满分4分）某校八年级将举行班级乒乓球对抗赛，每个班必须选派出一对男女混合
双打选手参赛．八年级一班准备在小娟、小敏、小华三名女选手和小明、小强两名男选手
中，选男、女选手各一名组成一对参赛. （1）请画出树状图或用列表法分析可能出现的
情况；（2）如果小敏和小强的组合是最强组合，那么采用随机抽签的办法，恰好选出小敏
和小强参赛的概率是多少？
七、
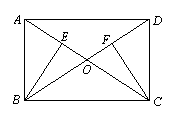（本题满分5分）如图，矩形ABCD中，AC与BD交于O
点，BE⊥AC于E，CF⊥BD于F. 求证：BE=CF.
八、
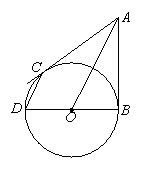（本题满分6分）如图，从⊙O外一点A作⊙O的切线AB、AC，
切点分别为B、C，⊙O的直径BD为6，连结CD、AO.
（1）求证：CD∥AO；
（2）设CD＝x，AO＝y，求y与x之间的函数关系式，并写出
自变量x的取值范围；
（3）若AO＋CD＝11，求AB的长.
九、（本题满分6分）某博物馆每周吸引大量中外游客前来参观，如果游客过多对馆中的珍贵
文物会产生不利影响，但同时考虑到文物的修缮和保护费用问题，还要保证一定的门票收
入，因此，博物馆采取了上浮门票价格的方法来控制参观人数，在该方法实施过程中发现：
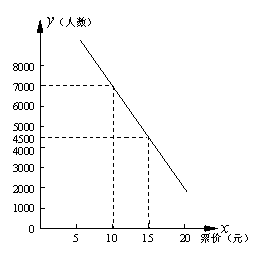
每周参观人数(y)与票价(x)之间存在如图所示的一次函数关系. (1)在这种情况下，如果
要确保每周收入4万元，门票价格应定为多少元?（2）若不限制参观的人数，问当门票价
格定为多少元时，门票收入最多？最多为多少元？
 |
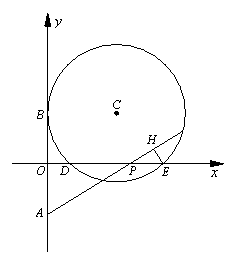
十、（本题满分9分）在坐标平面内，半径为R的⊙C与x轴交于点D（1，0）、E（5，0），与y轴的正半轴相切于点B. 点A、B关于x轴对称，点P（a，0）在x轴的正半轴上运动，作直线AP，作EH⊥AP于H.
（1）求圆心C的坐标及半径R的值；
（2）△POA和△PHE随点P的运动而变化，若它们全等，求a的值；
（3）若给定a=6，试判定直线AP与⊙C的位置关系，并说明理由.
