初中毕业生学业考试数学试卷2
（考试时间120分钟，满分120分）
第I卷（选择题 共15分）
一、选择题（每小题3分，共15分）
1、甲地的海拔高度为5米，乙地比甲地低7米，乙地的海拔高度为
A、－7米 B、－2米 C、2米 D、7米
2、下列事件是必然发生事件的是
A、打开电视机，正在转播足球比赛；
B、 小麦的亩产量一定为1000公斤；
C、在只装有5个红球的袋中摸出1球，是红球；
D、农历十五的晚上一定能看到圆月．
3、下面有4个汽车标致图案，其中是轴对称图形的是
① ② ③ ④
A、②③④ B、①③④ C、①②④ D、①②③
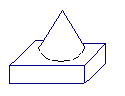4、下图中①表示的是组合在一起的模块，在②③④⑤四个图形中，是这个模块的俯视图的是
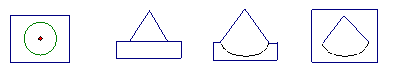
① ② ③ ④ ⑤
A、② B、③ C、④ D、⑤
5、用一水管向图中容器内持续注水，若单位时间内注入的水量保持不变，则在注满容器的过程中，容器内水面升高的速度
A、保持不变 B、越来越慢
C、越来越快 D、快慢交替变化
第II卷（非选择题 共105分）
二、填空题（每小题3分，共30分）
6、2004年12月国家统计局公布了西部地区的主要经济指标，其中四川省的工业增加值为155 000 000 000元，用科学记数法表示为__________________________________元．
7、计算：
＝__________________
8、分解因式：4
－1＝___________________________________
9、在函数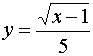
中，自变量
的取值范围是_____________________
10、不等式2－≥3的解集是___________________________
11、绕一定点旋转180°后与原来图形重合的图形是中心对称图形，正六边形就是这样的图形．小明发现将正六边形绕着它的中心旋转一个小于180°的角，也可以使它与原来的正六边形重合，请你写出小明发现的一个旋转角的度数：_____________________
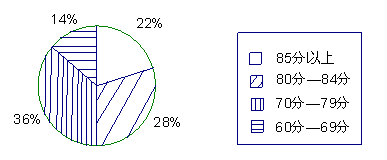12、如图是某校九年级一班50名学生的一次数学测验成绩的扇形统计图，按图中划分的分数段，这次测验成绩中所占百分比最大的分数段是_________________；85分以上的共有____________人．
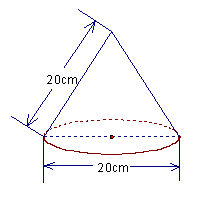
13、如图是学生小明自制的一个无底圆锥形纸帽的示意图，围成这个纸帽的面积（不计接缝）是____________________cm
（
取3．14，结果精确到十位）
14、用长度一定的绳子围成一个矩形，如果矩形的一边长（m）与面积
（m）满足函数关系
（0＜＜24），则该矩形面积的最大值为______________________
m．
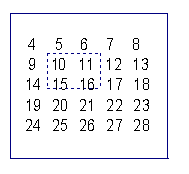
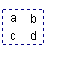15、如图是一个数表，现用一个矩形在数表中
任意框出4个数则
（1）a、c的关系是：__________________；
（2）当a＋b＋c＋d＝32时，a＝__________．
三、（第16题15分，第17题—第19题每题5分，共30分）
16、解答下列各题（每小题5分，共15分）：
（1）计算：
－－2
＋
tan60°．
（2）化简：
．
（3）解方程：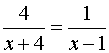
．
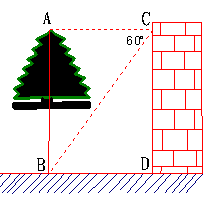17、如图，小勇想估测家门前的一棵树的高度，他站在窗户C处，观察到树顶端A正好与C处在同一水平线上，小勇测得树底B的俯角为60°，并发现B点距墙脚D之间恰好铺设有六块边长为0．5米的正方形地砖，因此测算出B点到墙脚之间的距离为3米，请你帮助小勇算出树的高度AB约多少米？（结果保留1位小数；参考数据：
，
）
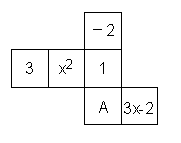18、右图是一个正方体的展开图，标注了字母A的面是正方体的正面，如果正方体的左面与右面所标注代数式的值相等，求的值．
19、下表是某市2004年城市居民收支情况抽样调查表，阅读表内信息，完成下列问题：
| 项目 | 2004年（元） | 2003年（元） | 同比增长（%） | |
| 可支配收入 | 工薪收入 | 8077．85 | 6349．41 | 27．2 |
| 经营性收入 | 289．77 | 222．53 | 30．2 | |
| 财产性收入 | 110．92 | 59．93 | 85．1 | |
| 转移性收入 | 3118．97 | 3353．76 | －7．0 | |
| 小计 | 11597．51 | 9985．63 | ||
| 消费支出 | 食品 | 3595．12 | 3060．34 | 17．5 |
| 衣着 | 800．72 | 699．14 | 14．5 | |
| 家庭设备用品及服务 | 484．00 | 419．95 | 15．3 | |
| 医疗保健 | 715．17 | 689．22 | 3．8 | |
| 交通和通讯 | 936．31 | 708．32 | 32．2 | |
| 教育文化娱乐服务 | 1099．44 | 1094．92 | 0．4 | |
| 居住 | 623．13 | 732．98 | －15．0 | |
| 杂项商品和服务 | 417．87 | 355．03 | 17．7 | |
| 小计 | 8671．76 | 7759．90 | ||
（1）说明该市城市居民可支配收入的主要来源是什么收入．
（2）该市城市居民可支配收入中同比增长最快的是哪项收入？
（3）从该市城市居民在消费支出方面的信息，你能得出哪些结论？试写出其中的两条．
四、（每小题7分，共21分）
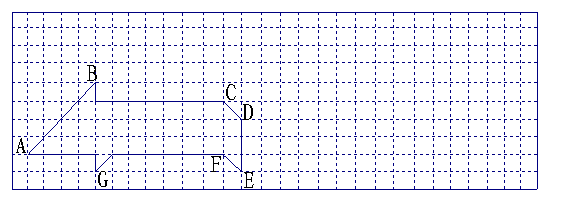20、下面的方格纸中，画出了一个“小猪”的图案，已知每个小正方形的边长为1．
（1）“小猪”所占的面积为多少？
（2）在上面的方格纸中作出“小猪”关于直线DE对称的图案（只画图，不写作法）；
（3）以G为原点，GE所在直线为x轴，GB所在直线为y轴，小正方形的边长为单位长度建立直角坐标系，可得点A的坐标是（_______，_______）．
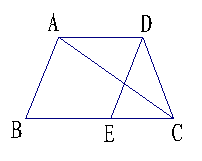
21、如图，梯形ABCD中，AD∥BC，AB＝DC，∠ADC＝120°，对角线CA平分∠DCB，E为BC的中点，试求△DCE与四边形ABED面积的比．
22、某校八年级将举行班级乒乓球对抗赛，每个班必须选派出一对男女混合双打选手参赛．八年级一班准备在小娟、小敏、小华三名女选手和小明、小强两名男选手中，选男、女选手各一名组成一对参赛，一共能够组成哪几对？如果小敏和小强的组合是最强组合，那么采用随机抽签的办法，恰好选出小敏和小强参赛的概率是多少？
五、（每小题8分，共16分）
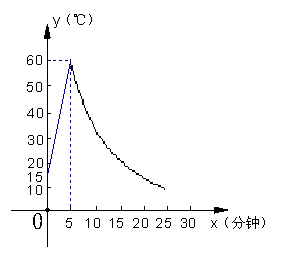23、制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．
（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；
（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？
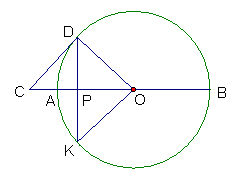24、如图，P是⊙O的半径OA上的一点，D在⊙O上，且PD＝PO．过点D作⊙O的切线交OA的延长线于点C，延长DP交⊙O于K，连接KO，OD．
（1）证明：PC＝PD；
（2）若该圆半径为5，CD∥KO，请求出OC的长．
六、（本题共8分）
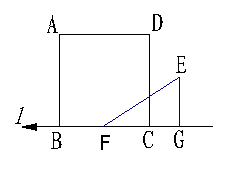25、如图，正方形ABCD的边长为5cm，Rt△EFG中，∠G＝90°，FG＝4cm，EG＝3cm，且点B、F、C、G在直线
上，△EFG由F、C重合的位置开始，以1cm/秒的速度沿直线按箭头所表示的方向作匀速直线运动．
（1）当△EFG运动时，求点E分别运动到CD上和AB上的时间；
（2）设x（秒）后，△EFG与正方形ABCD重合部分的面积为y（cm），求y与x的函数关系式；
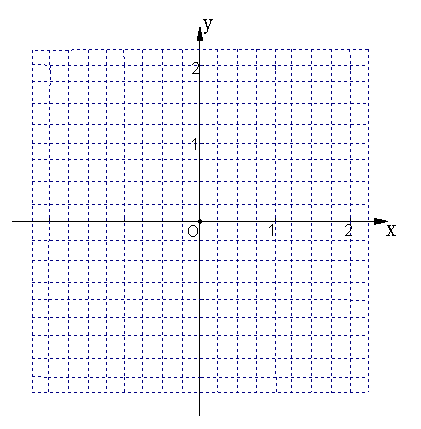（3）在下面的直角坐标系中，画出0≤x≤2时（2）中函数的大致图象；如果以O为圆心的圆与该图象交于点P（x，
），与x轴交于点A、B（A在B的左侧），求∠PAB的度数．