初中升学数学统一考试试题(三)
数 学
一、填空题（本大题共12小题，每小题2分，共24分）。
1、－3的绝对值是 。
2、请观察下面一列有规律的数：
根据此规律第99个数应为 。
3、分解因式：
。
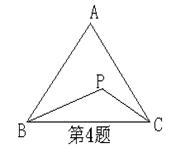
4、如图△ABC中，AB=AC，P为△ABC内一点，且
∠PBC=∠ACP已知∠A=70°，则∠BPC= 度。
5、计算：
=
。
、若一组数据5，6，4，x，5，0的平均数是4，则这组数据的众数是
。
7、计算：
。
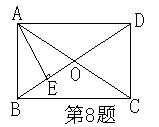
8、如图，矩形ABCD中，AC、BD相交于点O，AE⊥BD于E，若∠BAE：∠EAD=1：2，且OA=2，则AB的长为
。
9、在函数
中，自变量x的取值范围是
。
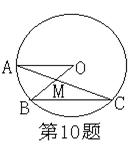
10、如图，在⊙O中，弦BC与半径OA平行，AC、OB相交于点M，若∠C=25°，则∠AMB= 度。
11、平安中学为了美化校园，决定在现有绿化面积的基础上，再增加5%。已知增加后，学校的绿化面积将达到37.8亩，则该校原有绿化面积为
亩。
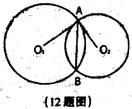
12、如图，⊙O1与⊙O2相交于A、B两点，O1A⊥O2A，已知O1A=4，O2A=3，则AB的长为 。
二、选择题（本大题共8小题，每小题3分，共24分），下列各题给出的四个选项中，只有一项是符合题目要求的。
13、已知Rt△ABC中，∠C=90°，BC=3，AB=5，则tanA之值为 （ ）
A、
B、
C、
D、
14、下列说法中，正确的是 （ ）
A、计算
的结果为
B、若
，则a=b
C、
都是无理数
D、把
写成科学计数法应为
15、一次函数
的图象不过
（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
16、已知Rt△ABC中，∠C=90°，BC=3，AC=4，则将Rt△ABC以AC边为旋转一周所得圆锥的侧面积为 （ ）
A、7.5π B、10π C、15π D、20π
17、下列图形既是中心对称，又是轴对称的是 （ ）
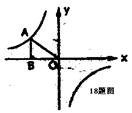18、如图，A为双曲线
上一点，AB⊥x轴于B，若
，则此双曲线的解
式为
（ ）A、
B、
C、
D
19、二元二次方程组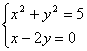
的解的组数为（ ）
A、1 B、2 C、3 D、4
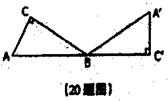20、如图，Rt△ABC中，∠C=90°，∠A=60°，AC=2，将△ABC绕点B沿顺时针方向旋转至△A’B’C’的位置，且使A´、B´、C’
三点在同一直线上，则点A所经过的最短路线的长为
（ ）
A、
B、
C、
D、
三、解答题（本大题10小题，共72分）解答本题时，要求写出主要的计算或论证步骤。
21、（本题6分）先化简，再求值：
22、（本题6分）用换元法解方程：
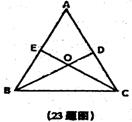
23、（本题6分）如图△ABC中，AB=AC，D、E分别为AC、AB的中点，BD、CE，相交于点O。求证：OB=OC
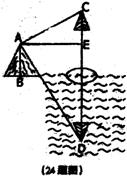24、（本题6分）如图，湖边有一座小山，现在小山的顶部A测得湖中一个小岛上的一棵树的树梢C的仰角为30°，同时测得树梢在湖水中的像D的俯角为60°。若山顶A到该树的水平距离AE为20米，求山高AB为多少？（观察时湖水是平静的，且计算结果保留根号）
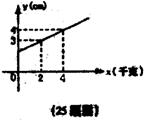25、（本题6分）已知一挂重不超过10千克的弹簧，其长度y(cm)与挂重x（千克）之间的函数关系如图所示，请根据图象回答下列问题（不必写出过程）
(1)y与x的函数关系式为 ；
(2)自变量x的取值范围为 ；
(3)弹簧本身的长度为 cm; (4)当挂重为6千克时，弹簧的长度为 cm。
26、(本题6分)已知二次函数
的图象与x轴交于A、B两点。
(1)求k的取值范围；
(2)若
=
，求k的值。
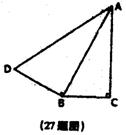
27、(本题8分)如图Rt△ABC中，∠C=90°，BC=1，AB=
，BD⊥AB于B，连结AD，若以A、B、D为顶点的三角形与△ABC相似，求AD的长。
28、（本题8分）如图，AB是⊙O的直径，△BCD内接于⊙O，CG⊥AB于E，BD、GC的延长线相交于点F。
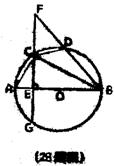求证：（1）△BFC~△BCD； （2）若BD=3，
，AC=2，求⊙O的半径为R。
29、（本题8分）李大妈家附近有一水果零售点，其中苹果每千克售价3元；距李大妈家较远处有一水果市场，其中苹果每千克售价2.5元。已知从李大妈家去水果市场返往一次的车费是6元。现李大妈准备购买一定数量的苹果，若不考虑其他因素，请帮李大妈计算一下，她应在水果零售点购买苹果还是在水果市场购买苹果更省钱。（假设只能乘车去水果市场）
30、（本题12分）已知二次函数
的图象过点A（2、0），且与直线
相交于B、C两点，点B在x轴上，点C在y轴上。
（1）求二次函数的解析式；
（2）若P（x，y）是线段BC上的动点，O为坐标原点，试求△POA的面积S与x之间的函数关系式，并求出自变量x的取值范围；
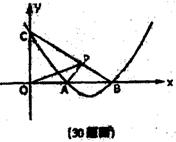（3）是否存在这样的点P，使PO=AO？若存在，求出P点的坐标；若不存在，请说明理由。