初中升学统一考试数学试题（二）

初中升学统一考试数学试题（二）

一、填空题（本大题共12小题，每小题2分，共24分）

1、-9的相反数是　　 。

2、分解因式　　　　  。

3、今年5月15日，我国用“长征四号乙”运载火箭成功地将两颗卫星送入离地面870千米的轨道。用科学记数法表示870千米＝　　  米。（保留两位有效数字）

4、如果x＜1，化简　　　　　　 。

5、在函数中，自变量x的取值范围是　　　　 。

6、已知等腰三角形的一边等于4，一边等于7，则它的周长是　　　 。

7、已知：△ABC中，∠ACB=90°,CD⊥AB于D，∠A＝30°，AB＝4cm，则BD＝　　cm.

8、计算： 　　　　　　.

9、甲、乙两同学进行射击水平测试，在相同条件下各射耙10次，命中环数如下：

甲：8，7，8，6，6，5，9，10，7，4；乙：9，8，7，6，5，7，8，6，7，7。为选拔其中一名射击水平比较稳定的同学参加射击比赛，则应选　　　　参赛。

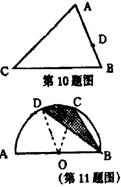
10、如图：△ABC中，D是AB上的一点，过D作一条直线e截△ABC，使截得的三角形与△ABC相似（不写作法）。e与△ABC的边的位置关系（或所成角与ABC的角的数量关系）是：　　　　　　　　 。

11、如图：已知半圆的直径AB＝60mm，弦DC//AB，∠DBC＝20°，则图中阴影部分的面积等于　　mm²（π取3.14）

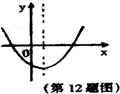12、二次函数的图象如图所示，则反比例函数的图象的两个分支分别在第　　象限。

二、选择题（本大题共8小题，每小题3分，共24分）

下列各题给出的四个选项中， 只有一项是符合题目要求的。

13、在2，-3，-5，6这四个数中，任取两个数相乘，所得的积中最大的是（　　）

A、12　　　　B、15　　　　C、18、　　　　D、-30

14、在△ABC中，∠BAC的平分线交BC于D，∠B＝60°，∠C＝50°，则∠ADC等于（　　 ）

A、50°　　　　 B、60°　　　 C、85°　　　 D、95°

15、顺次连结等腰梯形各边的中点，所得到的四边形的一定是（　　 ）

A、等腰梯形　　　B、矩形　　  C、菱形　　　D、正方形

16、某农户响应应退耕还林政策，种桃树200棵，现进入收获季节，请5人各随意采摘4棵桃树上的桃子，分别称得质量如下（单位：千克）：95，100，105，102，98.若今年市场上桃子售价为每千克2元，根据样本平均数估计，今年该农户卖出所有桃子将收入（　　 ）

A、4万元　　 B、2万元　　 C、1万元　　　　D、5千元

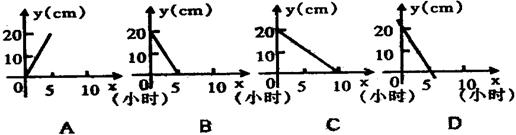17、一根蜡烛长20cm，点燃后每小时燃烧4cm，燃烧过程中蜡烛的高度y(cm)与燃烧时间x（小时）的函数关系，用图象表示为（　　 ）

18、下列方程中，有实数根的是（　　 ）

A、　 B、　　 C、　　 D、

19、在△ABC中，∠C＝90°，cosA=,则∠B等于（　　 ）

A、90°　　　　B、60°　　　C、45°　　D、30°

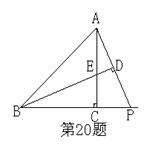
20、在△ABC中，∠ACB＝90°，∠ABC＝45°，P在BC延长线上从左向右移动，BD⊥AP于D，交AC于E，则移动过程中，BE与AP的大小关系为（　　 ）

A、BE＝AP　　　 B、BE＞AP　　　C、BE＜AP　　　D、无法确定

三、解答题（本大题共10小题，共72分）

解答本题时，要求写出主要的计算或论证步骤。

21、（本题6分）计算：

22、（本题6分）解不等式组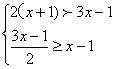，并把它的解集在数轴上表示出来，

23、（本题6分）阅读下面一段材料并解答所提出的问题。

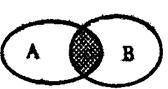
一般地，某些指定的对象汇集在一起就成为一个集合，集合中每一个对象叫做这个集合的元素。我们用大写字母A、B、C…….表示集合，用小写字母a、b、c……表示集合中的元素，记为A＝。两个集合A与B的公共部分（如图中的阴影部分）叫做集合A与B的交集，记为；AB

例如：A＝，A与B的公共部分是元素3，5.那么由3，5组成的集合叫A与B的交集，记为AB＝。请解答下面两个问题（直接写出结果）

1已知则AB

（2）已知则AB＝

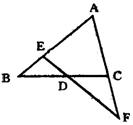
24、（本题6分）如图，△ABC中，D是BC的中点，过D的直线交AB于点E，交AC的延长线于点F。求证：

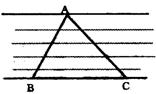25、（本题6分）在数学活动课上，老师带领学生去测河宽。如图，河对岸A点有一棵树，某学生在河这边沿河岸取两点B、C分别观测点A，使得∠ABC＝60°，∠ACB＝45°，量得BC＝20米。求这段河的宽度（取结果精确到0.1米）。

26、（本题6分）已知四边形ABCD，从①AB//DC；②AB＝DC；③AD//BC；④AD＝BC；⑤∠A＝∠C；⑥∠B＝∠D中任取两个条件加以组合，共有15种组合方式，请写出6种能推导出四边形ABCD的平行四边形的组合的代号：

（1）　　　　，（2）　　　　，（3）　　　　，（4）　　　　，（5）　　　　，（6）　　　　。

27、（本题8分）《遵义日报》2001年4月19日报道，遵义市第五次人口普查时总人口约为650万人。预计一年后城镇人口将增加0.7％，农村人口将增加1.09％，这样全市人口将增加1％。求遵义市第五次人口普查时城镇人口和农村人口各是多少万人？

28、（本题8分）已知，关于x的方程

（1）　　　 求证：无论 k为何值，方程总有两个不相等的实数根；

（2）　　　 若方程的两个根分别为x₁,x₂且求k的值。

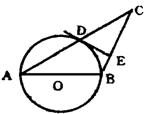
29、（本题8分）如图，以AB为直径的⊙O过AC的中点D，⊙O的切线DE交BC于点E。

求证：（1）AB＝BC；　 （2）DE⊥BC；　　 （3）CD²＝AB·CE

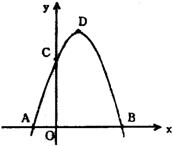
30、(本题12分)如图，已知抛物线与x轴交于A，B两点，与y轴交于点C，顶点为D。

（1）求A，B，C，D四点的坐标；

（2）一动点M在x轴上方的抛物线上移动，是否存在某个位置，使△MAB的面积最大？若存在，求出这个面积；若不存在，请说明理由；

（3）在x轴上作一点P，使得PD＋PC最小。（不写作法，保留作图痕迹）