圆

新课标(北师大版)中考数学第一轮复习测试卷

第十六单元　圆

一、选择题(每小题4分，共40分)

1、已知在⊙O中，弦AB的长为8厘米,圆心O到AB的距离为3厘米, 则⊙O的半径是（　C　 ）

A.3厘米　　 　　　 B. 4厘米　 　　C. 5厘米　　　　　　D. 8厘米

2、△ABC内接于⊙O，∠ACB＝36°，那么∠AOB的度数为（　C　）

A．36°　　　　B．54°　　　　 C．72°　　　　D．108°

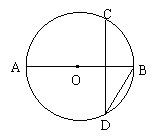
3、如图，AB是⊙O的直径，弦CD垂直平分OB，则∠BDC=（　C　）

A.15°　　 B.20°　　 C.30°　　 D.45°

4、在半径为2a的⊙O中，弦AB长为2a，则∠AOB为（　B　 ）

A.90°　　 B.120°　　 C.135°　　 D.150°

5、在△ABC中，∠ABC=30°，AB=10，那么以A为圆心，6为半径的⊙A与直线BC的位置关系是（　A　 ）

A. 相交　　 B. 相切　　C. 相离　　D. 不能确定

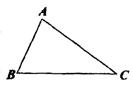
6、如图所示，已知△ABC中，AB＜AC<BC．求作：一圆的圆心O0，使得O在BC上，且圆O与AB、AC都相切．下列四种作法中，正确的是（　B　 ）

A.作BC的中点O

B.作∠A的平分线交BC于O点

C.作AC的中垂线，交BC于O点

D.自A点作一直线垂直BC，交BC于O点

7、Rt△ABC中，∠Ｃ＝90°，AC=3cm，BC=4cm。给出下列三个结论：①以点C为圆心,2.3cm长为半径的圆与AB相离；②以点C为圆心,2.4cm长为半径的圆与AB相切；③以点C为圆心,2.5cm长为半径的圆与AB相交。则上述结论中正确的个数是（　D　 ）

A.0个　　B.1个　　C.2个　　 D.3个

8、⊙O的半径为2，点P是⊙O外一点，OP的长为3，那么以P为圆心，且与⊙O相切的圆的半径一定是（　A　 ）

A.1或5　　　　　  B.1　　　　  C.5　　　　　  D.1或4

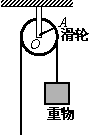9、如果圆锥的底面半径为3cm，母线长为4cm，那么它的侧面积等于（　B　 ）

A.24πcm²  B.12πcm²  C.12cm² D.6πcm²

10、一个定滑轮起重装置如图所示，滑轮的半径是10cm，当重物上升10cm时，滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度约为(假设绳索与滑轮之间没有滑动，结果精确到1°)（　C　 ）

A.115°　　 B.60°　　 C.57°　　 D.29°

二、填空题(每小题4分，共40分)

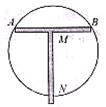
11、如图，MN所在的直线垂直平分线段AB，利用这样的工具，最少使用　 2　 次，就可以找到圆形工件的圆心.

(第11题图)　　　　　　 (第12题图)　　　　　　　  (第15题图)

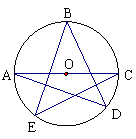
12、如图，A、B、C、D、E均在⊙O上，且AC为⊙O的直径，则∠A+∠B+∠C=_90__度.

13、已知⊙O的半径为10，弦AB=12，如果M是所有经过A、B两点的圆中最小的一个，那么圆心距MO=　 8　　 .

14、已知⊙O₁的半径为6cm，⊙O₂的半径为2cm，O₁O₂=8cm，那么这两圆的位置关系是　外切 .

15、如图，粮仓的顶部是圆锥形，这个圆锥底面周长为32m，母线长为7m，为防雨需要在粮仓顶部铺上油毡，则共需油毡　　112　　　　 m²（油毡接缝重合部分不计）.

三、(每小题8分，共16分)

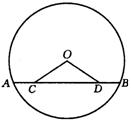16、如图，AB是⊙O的弦（非直径），C、D是AB上的两点，并且AC＝BD．

求证：OC＝OD．

证明略

17、等腰三角形的腰长为13cm，底边长为10 cm，求它的外接圆的半径。

四、(每小题9分，共18分)

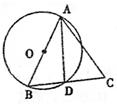18、如图，在△ABC中，以AB为直径的⊙O交BC于D，连结AD，请你添加一个条件，使△ABD≌△ACD，并加以证明.

你添加的条件是　　　　　　 。

证明：

条件：∠BAD=∠CAD或AB=AC　 证明：略

19、用圆规、直尺（三角尺）作图，不写作法，但要保留作图痕迹.

如图，AB、CD是两条互相垂直的公路，设计时想在拐变处用一段圆弧形弯道把它们连接起来（圆弧在A、C两点处分别与道路相切），测得AC=60米，∠ACP=45°.

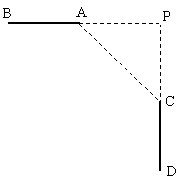(1)在图中画出圆弧形弯道的示意图；

(2)求弯道部分的长.(结果保留四个有效数字).

(1)图略　(2)66.64米

五、(每小题10分，共20分)

20、如图,AB是⊙O的直径, ⊙O过BC的中点D,DE⊥AC.

求证：(1) △BDA∽△CED.

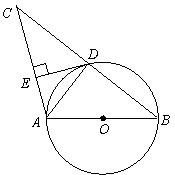(2)DE是⊙O的切线.

证明略

21、一平面内，已知点O到直线l的距离为5，以点O为圆心，r为半径画圆.探究、归纳：

（1）当r=__________时，⊙O上有且只有一个点到直线l的距离等于3.

（2）当r=_________时，⊙O上有且只有三个点到直线l的距离等于3.

（3）随着r的变化，⊙O上到直线l的距离等于3的点的个数有哪些变化？并求出相对应的r的值或取值范围（不必写出计算过程）.

（1）r=2.（2）r=8. （3）当0<r<2时，⊙O上没有点到直线l的距离等于3；当r=2时，⊙O上有且只有1个点到直线l的距离等于3；当2<r<8时，⊙O上有且只有2个点到直线l的距离等于3；当r=8时，⊙O上有且只有3个点到直线l的距离等于3； 当r>8时，⊙O上有且只有4个点到直线l的距离等于3.

六、(本题12分)

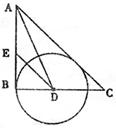22、如图，在Rt△ABC中，∠B=90°，∠A的平分线交BC于D，E为AB上一点，DE=DC，以D为圆心，以DB的长为半径画圆。

求证：（1）AC是⊙D的切线；

（2）AB+EB=AC。

（1）过点D作DF⊥AC于F

∵AB为⊙D的切线　AD平分∠BAC　∴BD=DF

∴AC为⊙D的切线

　 （2）在△BDE和△DCF中　∵BD=DF　DE=DC

∴△BDE≌△DCF（HL）　∴EB=FC

又AB=AF　∴AB+EB=AF+FC　即AB+EB=AC

七、(本题12分)

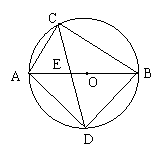23、已知在⊙O中，直径AB为10 cm，弦AC为6 cm，∠ACB的平分线交⊙O于D，交AB于E.

(1)求BC、AD和BD的长；

(2)求证：AD²=DE·DC.

(1)BC=8cm，AD=BD=5cm　(2)证明略

八、(本题12分)

24、如图,B为线段AD上一点,△ABC和△BDE都是等边三角形,连结CE并延长交AD的延长线于点F,△ABC的外接圆⊙O交CF于点M.

（1）求证：BE是⊙O的切线；

（2）求证：AC²＝CM·CF；

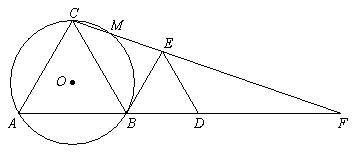（3）若过点D作DG∥BE交EF于点G,过G作GH∥DE交DF于点H,则易知△DGH是等边三角形.设等边△ABC、△BDE、△DGH的面积分别为S₁、S₂、S₃,试探究S₁、S₂、S₃之间的等量关系,请直接写出其结论.

（1）证明：连结OB　

∵△ABC和△BDE都是等边三角形

∴AB＝BC＝AC　，∠CAB＝∠ABC＝∠EBD＝60°

且∠OBC＝30°

又∠CBE＝180°－60°－60°＝60°

∴∠OBE＝30°＋60°＝90°　即OB⊥BE

∴BE是⊙O的切线

（2）证明：（方法一）连结AM

则∠AMC＝∠ABC＝∠CAF＝60°

又∠ACM＝∠FCA

∴△ACM∽△FCA　　　

∴　　∴

（方法二）连结BM，证△BCM∽△FCB（略）

（3）或