新课标(北师大版)中考数学第一轮复习测试卷
第二单元 整式及其运算
一、选择题(每小题4分，共40分)
1、下列两项中，属于同类项的是（ D ）
A.62与x2 B．4ab与4abc C．0.2x2y与0.2xy2 D．mn与-mn
2、化简(-x)3(-x)2，结果正确的是（ C ）
A．-x6 B．x6 C．-x5 D．x5
3、下列运算正确的是( D )
A．2x＋3y＝5xy B．4x4y2－5xy2＝－x2y
C．3x－2·2x3＝6x－6 D．4x4y2÷(－2xy2)＝－2x3
4、某种商品进价为a元/件，在销售旺季，商品售价较进价高30%；销售旺季过后，商品又以7折（即原售价的70%）的价格开展促销活动，这时一件该商品的售价为（ D ）
A. a元 B.0.7 a元 C.1.03 a元 D.0.91a元
5、下列运算正确的是（ D ）
A.(a+b)2=a2+b2 B.(a-b)2=a2-b2 (03滨州)
C.(a+m)(b+n)=ab+mn D.(m+n)(-m+n)= -m2+n2
6、已知a-b=2
-1，ab=，则(a+1)(b-1)的值为（ A ）
A.-
B.3
C.3-2
D.-1
7、下列多项式能因式分解的是（ D ）
A.x2-y B.x2+1 C.x2+xy+y2 D.x2-4x+4
8、把a3－ab2分解因式的正确结果是（ C ）
A (a+ab)(a－ab) B a (a2－b2)
C a(a+b)(a－b) D a(a－b)2
9、一家商店以每包a元的价格进了30包甲种单枞茶，又以每包b(b>a)元的价格买进60包乙种单枞茶。如果以每包
元的价格卖出这两种茶叶，则卖完后，这家商店（ B ）
A、赚了 B、赔了 C、不赔不赚 D、不能确定赔或赚
10、观察下列数表：
1 2 3 4 … 第一行
2 3 4 5 … 第二行
3 4 5 6 … 第三行
4
5
6
7 … 第四行
根据数表所反映的规律，第n行第n列交叉点上的数应为（ A ）
A.2n-1 B.2n+1 C.n2-1 D.n2
二、填空题(每小题4分，共40分)
11、
x2y的系数是 ，次数是 3 .
12、已知x+y=1，那么
x2+xy+y2的值为 .
13、如果(2a+2b+1)(2a+2b-1)=63，那么a+b的值为_____±4_______.
14、为鼓励节约用电,某地对居民用户用电收费标准作如下规定：每户每月用电如果不超过100度,那么每度电价按a元收费;如果超过100度,那么超过部分每度电价按b元收费.某户居民在一个月内用电160度,他这个月应缴纳电费是 100a+60b 元（用含a、b的代数式表示）
15、观察下列等式
9-1=8
16-4=12
25-9=16
36-16=20
…………
这些等式反映自然数间的某种规律，设n(n≥1)表示自然数，用关于n的等式表示这个规律为
(n+2)2-n2=4(n+1) .
三、(每小题8分，共16分)
16、分解因式：
(1) (x+y)(x2+y2)-2y2(x+y) (2)(a2+b2)2-4a2b2
(1)(x+y)2(x-y) (2)(a+b)2(a-b)2
17、计算
(1)3x-(2y-x)+y (2)5a2-[a2+(5a2-2a)-2(a2-3a)]
(1)4x-y (2)a2-4a
四、(每小题9分，共18分)
18、化简：(
a4b7-
a2b6)÷(-
ab3)2
6a2b-1
19、先化简，再求值：(2x+y)(2x-y)+(x+y)2-2(2x2-xy)，其中x=1，y=1.5
x2+4xy=7
五、(每小题10分，共20分)
20、已知a，b是互为相反数，c，d是互为倒数，e是非零实数，求
(a+b)+
cd-2e0的值.
-1
21、已知实数a、b满足(a+b)2=7，(a-b)2=5，求a2+b2+ab的值.
1
六、(本题12分)
22、观察下面的点阵图和相应的等式，探究其中的规律：
（1）在④和⑤后面的横线上分别写出相应的等式；
 |
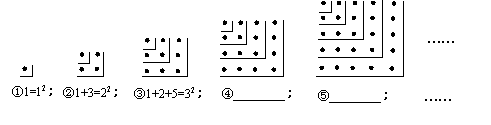（2）通过猜想写出与第n个点阵相对应的等式.
(1)④1+3+5+7=42；⑤1+3+5+7+9=5；(2)1+3+5+…+(2n-1)=n2.
七、(本题12分)
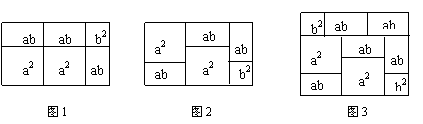23、我们已经知道，完全平方公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，例如：(2a+b)(a+b)=2a2+3ab+b2就可以用图1或图2等图形的面积来表示.
(1)请写出图3所表示的代数恒等式： .
(2)试画出一个几何图形，使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2.
(3)请仿照上述方法另写一个含有a、b的代数恒等式，并画出与之对应的几何图形.
(1)(2a+b)(a+2b)=2a2+5ab+2b2 (2)图略 (3)略
八、(本题12分)
24、先阅读下面的材料，然后解答问题：
在一条直线上有依次排列的n(n>1)台机床在工作，我们要设置一个零件供应站P，使这n台机床到供应站P的距离总和最小，要解决这个问题，先“退”到比较简单的情形：
如图①，如果直线上有2台机床时，很明显设在A1和A2之间的任何地方都行，因为甲和乙所走的距离之和等于A1到A2的距离.
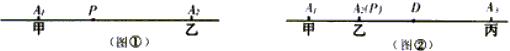
如图②，如果直线上有3台机床，不难判断，供应站设在中间一台机床A2处最合适，因为如果P放在A2处，甲和丙所走的路程之和恰好为A1到A3的距离，而如果把P放在别处，例如D处，那么甲和丙所走的距离之和仍是A1到A3的距离，可是乙还得走从A2到D的这一段，这是多出来的，因此P放在A处是最佳选择.
不难知道，如果直线上有4台机床，P应设在第2台与第3台之间的任何地方；有5台机床，P应设在第3台位置.
问题(1)：有n台机床时，P应设在何处？
当n为偶数时，P用设在第
台和第(+1)台之间的任何地方；当n为奇数时，P应设在第
台的位置.
问题(2)：根据问题(1)的结论，求x–1+x–2+x–3+……+x–617的最小值.
根据绝对值的几何意义，求的最小值，就是在数轴上找出表示x的点，使达到表示1，2，，…，617各点的距离之和最小。根据问题(1)的结论，当x=309时，原式的值最小，最小值是：∣309-1∣+∣309-2∣+…+∣309-308∣+∣309-309∣+∣309-310∣+∣309-311∣+…+∣309-616∣+∣309-617∣=308+307+…+1+1+2+……+308=308×309=95172