第七单元 视图与投影
直角三角形的边角关系
Ⅰ.考点透视
一、视图与投影
1.视图(长方体、正方体的展开图，直棱柱、圆柱、圆锥、球的三视图——主、俯视图要长对正，主、左视图要高平齐，左、俯视图要宽相等)
例1、一几何体的三视图如下，请你画出这个几何体.
 |
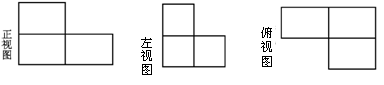2.投影(平行投影、中心投影、盲区)
例2、下列命题正确的是（ ）
A.三视图是中心投影 B.小华观察牡丹话，牡丹花就是视点
C.球的三视图均是半径相等的圆 D.阳光从矩形窗子里照射到地面上得到的光区仍是矩形
二、直角三角形的边角关系
1.在Rt△ABC中，∠C为直角，∠A、∠B为锐角，它们所对的边分别为c 、a、b ，其中除直角c外，其余的5个元素之间有以下关系：
(1)三边之间的关系：
(2)锐角之间的关系：
(3)边角之间的关系：
2.特殊角的三角函数值：
| 30º | 45º | 60º | 函数值增减情况 | |
| sinA | ||||
| cosA | ||||
| tanA |
3.解直角三角形的四种情况
在Rt△ABC中，∠C=90°：
(1)已知∠A、c，则a=__________;b=_________。
已知一锐角、斜边，求对边，用锐角的正弦；求邻边，用锐角的余弦。
(2)已知∠A、b，则a=__________;c=_________。
已知一锐角、邻边，求对边，用锐角的正切；求斜边，用锐角的余弦。
(3)已知∠A、a，则b=__________;c=_________。
已知一锐角、对边，求邻边，用锐角的余切；求斜边，用锐角的正弦。
(4)已知a、b，则c=__________。
(5)已知a、c，则b=__________ 。
4.仰角与俯角、坡度
(1) 线与 线所成的角中，视线在水平线上方的角叫 ，视线在水平线下方的角叫 .
(2)坡度：i＝ 高度∶ 宽度＝tanα(α坡角)＝
。
例3、(1)在离电视塔m米的A处测得塔顶的仰角是α，则此电视塔的高为 .
(2)若菱形中较长的对角线与边长的比是
∶1，则菱形相邻的两内角为 .
(3)铁路路基横断面为一个等腰梯形，若腰的坡度为2∶3，顶宽为3米，路基高为4米，则路基的下底宽是 .
(4)平行四边形ABCD中，AB＝10，BC＝15，∠B＝60°，则它的面积是＿＿.
(5)已知在一段坡面上，铅直高度为
，坡面长为2，则坡度i为____,坡角α为 .
(6)在Rt△ABC中，∠C＝90°，∠A＝15°，AB的垂直平分线与AC相交于M，则CM∶MA＝ .
(7)在Rt△ABC中，∠C＝90°，tanA=3，AC=10，则△ACB的面积是 .
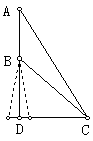例4、如图，山顶B处有一铁塔AB，在塔顶A处测得地面上一点C的俯角α=60°，在塔底B处测得点C的俯角β＝45°，已知塔高AB＝30米，求山高BD。
Ⅱ.中考演练
一、选择题(每小题4分，共40分)
1、下面的图形中是正方体展开图的有（ ）
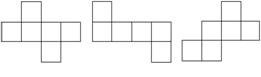
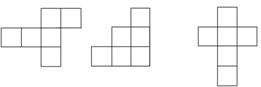
A.3个 B.4个 C.5个 D.6个
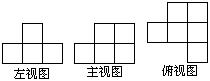
2、右图是由一些相同的小正方体构成的几何体的三视
图，则构成这个几何体的小正方体的个数是（ ）
A.5 B.6 C.7 D.8
3、小李身高1.80m，小王身高1.65m，他们在同一时刻站在阳光下，小李的影子长为1.20m，则小王的影长为（ ）
A.1.00m B.1.05m C.1.10m D.1.15m
4、已知tan(90°-α)=
，则锐角α的度数是（ ）
A.60° B.45° C.30° D.75°
5、将Rt△ABC的各边都扩大4倍，则锐角A的余弦值（ ）
A.不变 B.扩大4倍 C.原来的0.25 D.不能确定
6、在Rt△ABC中，∠C＝90°，若AB＝2AC，则cosA=（ ）
A
B
C
D
7、在△ABC中，∠C＝90°，cosB=
，则a∶b∶c＝（ ）
A.1∶2∶3 B.1∶
∶3 C.2∶
∶3 D.2∶∶
8、在Rt△ABC中，∠C=Rt∠，AC=1，AB=.则∠B为( )
A.30° B.45° C.60° D.90°
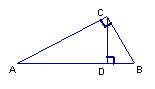9、如图在Rt△ABC中, ∠ACB=90°,CD⊥AB，D为垂足，若AC=4,BC=3，则sin∠ACD的值为( )。
A.
B.
C.
D.
10、△ABC中，∠A、∠B都是锐角，且sinA=
，cosB=
，则△ABC三个角的大小关系是（ ）
A.∠C>∠A>∠B B.∠B>∠C>∠A C.∠C>∠B>∠A D.∠A>∠B>∠C
二、填空题(每小题4分，共40分)
11、添线补全下面几何体的三视图
 | |||||||
 | |  | |||||
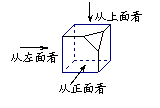主视图 左视图 俯视图
12、下面四幅图是两个物体不同时刻在太阳光下的影子，按照时间的先后顺序正确的排列应该是
.(填序号)
13、在Rt△ABC中，∠C＝90°，且sinA=
，则cosA=
，tanA= .
14、一个等腰三角形两边的长分别是3cm和6cm，则其底角的余弦值为 .
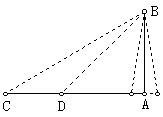15、如图为测量河岸一铁塔AB的高，先在C处测得塔顶A的仰角为30°，然后正对铁塔前进20米至D处，测得A的仰角为45°，则塔高AB= 米.
三、(每小题8分，共16分)
16、计算
(1)cos245°+tan60°cos30°
(2)
17、用小立方体搭一个几何体，使它的主视图和俯视图如图所示，俯视图中小正方形中字母表示在该位置小立方体的个数，请解答下列问题：
(1)请你画出这个几何体的一种左视图
(2)若组成这个几何体的小立方体的块数为n，请你写出n的所有可能值.
四、(每小题9分，共18分)
18、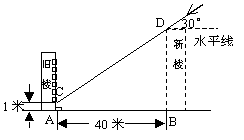
为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为40米，中午12时不能挡光.如图，某旧楼的一楼窗台高1米，要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射，并且光线与水平线的夹角最小为30°，在不违反规定的情况下，请问新建楼房最高多少米？（结果精确到1米.
，
）
19、电线杆上有一盏路灯O，电线杆与一排白杨树整齐划一地排列在马路的一侧，AB、CD、EF是三棵等高的白杨树，相邻的两棵树之间的距离都是2米，已知AB、CD在灯光下的影长分别为BM=1.6米、DN=0.6米.
(1)请画出路灯O的位置和白杨树C在路灯灯光下的影子；
(2)求白杨树EF的影长.
五、(每小题10分，共20分)
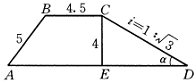20、如图，一段河坝的断面为梯形ABCD，试根据图中数据，求出坡角a和坝底宽AD．(i＝CE∶ED，单位米，结果保留根号)
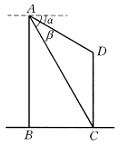21.如图，两建筑物的水平距离BC为24米，从点A测得点D的俯角a＝30°，测得点C的俯角b＝60°，求AB和CD两座建筑物的高．（结果保留根号）
六、(本题满分12分)
22、在旧城改造中，要拆出一烟囱AB，如图，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在从离B点21米的建筑物CD顶端C点测得A点的仰角为45°，B点的俯角为30°，问离B点35米远的保护文物是否在危险区内？
七、(本题满分12分)
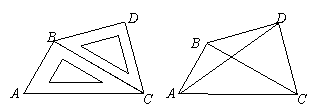
23、将一副三角尺如下图摆放在一起，连结
，试求
的正切值.
 |
八、(本题满分12分)
24、某校组织学生到涪江河某段测量两岸的距离，采用了两种方案收集数据．
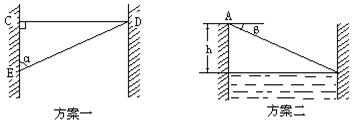方案一：如图，从C点找准对岸一参照点D，使CD垂直于河岸线
，沿河岸行走至E点，测出CE的长度后，再用电子测角器测出CE与ED的夹角α．
方案二：如图，先从河岸上选一点A，测出A到河面的距离h．再用电子测角器测出A点到对岸河面的俯角β．
(1)学生们选用不同的位置测量后得出以下数据，请通过计算填写下表：（精确到0.1米）
方案一 方案二
| 测量次数 | 1 | 2 | 3 |
| EC（单位：米） | 100 | 150 | 200 |
| α |
|
|
|
| 计算得出河宽（单位：米） |
| 测量次数 | 1 | 2 | 3 |
| h（单位：米） | 14.4 | 13.8 | 12.5 |
| β |
|
|
|
| 计算得出河宽（单位：米） |
(参考数据：tan1°24′=0.0244、tan2°16′=0.0396、tan1°56′=0.0338、tan76°33′=4.1814、tan71°35′=3.0032、tan65°25′=2.1859)
(2)由(1)表中数据计算：
方案一中河两岸平均宽为 米；
方案二中河两岸平均宽为 米；
(3)判断河两岸宽大约为 米；（从下面三个答案中选取，填入序号）
①390～420 ②420～450 ③350～480
(4)求出方案一的方差
和方案二的方差
，判断用那种方案测量的误差较小（精确到1）.