中考第一轮复习数与式
第一单元
Ⅰ. 考点透视
1、实数及其运算
(1) 实数的概念(有理数、无理数和实数，数轴，相反数，绝对值，倒数，科学记数法，精确度与有效数字)
例1、(1)(-2)3与-23（ ） A.相等 B.互为相反数 C.互为倒数 D.它们的和为16
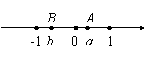(2)已知实数ab在数轴上对应的点如图所示.
①用“<”连接下列各数：a，b，-a，-b，1+a，-1-a，1-b
②化简：2b+2+b-a+1-a-b
(2)实数的运算(有理数的加、减、乘、除、乘方、开方运算法则，运算律及其运算顺序，实数大小比较的方法)
例2、(1) 计算
的结果是（ ）
A.4 B.3 C.2 D.1
(2)计算：①-22+(-2)3-[64-
(
)÷(-
)4]÷(-63) ②
+
-6
2、整式及其运算
(1)整式的概念(单项式、多项式和整式，同类项)
例3、(1)下列运算中正确的是( )
A.a2·a3=a5 B.(a2)3=a5 C.a6÷a2=a3 D.a5＋a5=2a10
(2)如图是某花圃摆放的一组花盆图案(“○”代表红花花盆，“×”代表黄花花盆).
 |
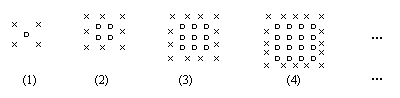观察图形并探索：在第n个图案中，红花和黄花的盆数分别是 .
(2)整式的运算(整式的加减运算—去括号，合并同类项、乘除及乘方运算法则—幂的运算性质、乘法公式及其几何背景)
例4、(1)先化简，再求值：5x2-(3y2+5x2)+(4y2+7xy)，其中x=-1，y=1-
(2) 化简求值：[(x-y)2+(x+y)(x-y)]÷2x，其中x=3，y= -1.5
3、因式分解(因式分解的概念，因式分解的方法—提取公因式法、运用公式法，因式分解的一般步骤)
例5、(1)分解因式：x3y2-4x= .
(2)请写一个三项式，使它先提取公因式，再用公式来分解因式。你写的三项式是 .
4、分式及其运算
(1)分式的概念(分式、分式有意义及值为零的条件，最简分式与最简公分母，通分和约分)
例6、(1)当x 时，分式
有意义.
(2)要使分式
的值为零，x的值应为（ ） A.2 B.-2 C.±2 D.0
(3)与分式相等的是（ ） A. B. C.- D.
(2)分式的运算(分式的基本性质，分式的加、减、乘、除、乘方运算法则及其运算顺序)
例8、(1)化简
的结果是（ ）A.m＋2 B.m－2 C.
D. 
(2)计算：①
②
Ⅱ.中考演练
一、选择题（每小题1分，30分）
1、下列说法中错误的是（ ）
A.相反数等于它本身的数只有零 B.±1的倒数等于它本身
C.若a为任意实数，则它的倒数是a－1 D.绝对值最小的整数是0
2、－24÷(－2)2=（ ）
A.4 B.－4 C.－2 D.2
3、长江三峡工程电站的总装机容量是千瓦，用科学记数法表示应记作（ ）
A．0.18×108千瓦 B．1.82×106千瓦
C．1.82×106千瓦 D．1.82×107千瓦
4、
的平方根是（ ）
A.3 B.±3 C.
D.±
5、若a―1+(b+1)2=0，则a2004+b2005的值是（ ）
A.0 B.2 C.－1 D.－2
6、若｜m｜=－m，则m是( )
A.正数 B.负数 C.非正数 D.非负数
7、在(1－
)0，sin45°，0.…，
，
这六个数中，无理数有( )
A.2个 B.3个 C.4个 D.5个
8、已知a<b<0，那么a、－b、a－b的大小关系是（ ）
A.－b>a>a－b B. a－b>a>－b C. a>－b>a－b D. a>a－b>－b
9、下列分式从左到右的变形中，正确的是 ( ).
A.
B.
C.
D.
10、化简(－a5)2+(－a2)5的结果是（ ）
A.0 B.2a10 C.－2a10 D.－a7
11、某商品原价a元，连续两次降价10%后的价格为（ ）
A.1.21a B. 0.81a C. a÷1.21 D. a÷0.81
12、若分式
的值为0时，x的值应为（ ）
A.x=±5 B.x=5 C. x=－5 D.x=0
13、若x2+2(m－3)x+16是完全平方式，则m的值是（ ）
A.11 B.－5 C.－7或1 D.7或－1
14、已知｜x=3，y=2，且x·y<0，则x+y的值等于（ ）
A 5或－5 B 1或－1 C 5或1 D－5或－1
15、实数a、b在数轴上的位置如图所示，则下列结论正确的是（ ）
A.a+b>a>b>a－b B. a>a+b>b>a－b C. a－b>a>b>a+b D. a－b>a>a+b>b
16、当x＝1时，代数式px3+qx+1的值为2005，则当x=－1时，代数式px3+qx+1的值为（ ）
A.－2004 B.－2005 C.2005 D.2004
17、随着计算机技术的迅猛发展，电脑价格不断降低，某品牌电脑按原售价降低m元后，又降低20%，现售价为n元，那么该电脑的原售价为（ ）
A.(0.8n+m)元 B.(1.25n+m)元 C.(5m+n)元 D.(5n+m)
18、某粮店出售的三种品牌的面粉袋上，分别标有质量为（25士0.1 ）kg、（25士0．2）kg、（25士0．3）kg的字样，从中任意拿出两袋，它们的质量最多相差（ ）
A.0．8kg B.0．6kg C.0．5kg D.0．4kg
19、小亮从一列火车的第m节车厢数起，一直数到第n节车厢（n＞m），他数过的车厢节数是（ ）
A.m＋n B.n－m C.n－m－l D.n－m＋1
20、设a是大于1的实数，若a，
，
在数轴上对应点分别记作A，B，C，则A，B，C三点在数轴上自左至右的顺序是（ ）
A. C，B，A B. B，C，A C. A，B，C D. C，A，B
21、如果a是 b的近似值，那么我们把b叫做a的真值．若用四舍五入法得到的近似数是85，则下列各数不可能是其真值的是（ ）
A.85.01 B.84.51 C.84.99 D.84.49
22、日常生活中我们使用的数是十进制数．而计算机使用的数是二进制数，即数的进位方法是“逢二进一”．二进制数只使用数字0、1，如二进制数1101记为1101(2)，1101(2)通过式子1×23+1×22+0×2+1可以转换为十进制数13，仿照上面的转换方法，将二进制数11101(2)转换为十进制数是（ ）
A.29 B.25 C.4 D.33
23、化简
的结果是（ ）
A.ab B.
C.
D.
23、买单价为a元的体温计n个，付出b元，应找回的钱数是（ ）
A.（b－na）元 B.（b－n）元 C.（na－b）元 D.（b－a）元
24、计算(x－y)(－y－x)的结果是（ ）
A.―x2―y2 B.―x2+y2 C.x2―y2 D.x2+y2
25、当x＝－2时，代数式-x2+2x-1的值等于（ ）
A.9 B.1 C.－9 D.－1
26、下列计算正确的是（ ）
A．a3·a2 = a5 B. a3÷a=a 3 C. (a2)3 = a 5 D. (3a)3 = 3a 3
27、用配方法将二次三项式a2+ 4a +5变形，结果是（ ）
A.(a–2)2+1 B.(a +2)2+1 C.(a –2)2-1 D.(a +2)2-1
28、计算
得（ ）
A.1
B.-1
C.
D.
29、现规定一种运算：a※b=ab+a―b，其中a、b为实数，则a※b+(b―a)※b等于（ ）
A.a2―b B.b2―b C.b2 D.b2―a
30、下面是某同学在一次测验中的计算摘录：①3a+2b=5ab ②
4m3n－5mn3=－m3n ③3x3•(－2x2)=－6x5 ④ 4a3b÷(－2a2b)=-2a ⑤ (a3)2=a5 ⑥ (－a)3÷(－a)=－a2,其中下确的个数有（ ）
A．1个 B．2个 C．3个 D．4个
二、填空题（每小题1分，共28分）
31、
的倒数的相反数是
.
32、计算：(＋1)＋(－2)＝ ；化简：a5b÷a3= .
33、若2xm―1y2与―x2yn是同类项，则(―m)n＝ .
34、一年定期的存款，年息为1.98％，到期取款时需扣除利息的20％作为利息税上缴国库，假如某人存入一年的定期储蓄2000元，到期后可得本息和是 元。
35、国家质检总局出台了国内销售的纤维制品甲醛含量标准，从2003年1月1日正式实施．该标准规定：针织内衣、被套、床上用品等直接接触皮肤的制品，甲醛含量应在百万分之七十五以下，百万分之七十五用科学记数法表示应写成 .
36、如果a<0，则｜a2÷(－a)=_______.
37、已知a+
=3,则a2+
=_________.
38、若｜a=3，
=2，且ab<0，则a－b= .
40、若x2+ax+b可分解因式为(x+1)(x－2)，则a＝ ，b= .
41、当x＝＿＿＿时，分式
无意义；当x＝＿＿＿时，分式的值为零。
42、分式
、
、
的最简公分母是 .
43、若两个分式
与
的和等于它们的积，则实数x的值为 .
44、观察下列等式：13＝12；13＋23＝32；13＋23＋33＝62；13＋23＋33＋43＝102，…。想一想，其中有什么规律，请把这种规律用等式写出来＿＿＿＿＿＿＿。
45、观察下列等式：9－1＝8；16－4＝12；25－9＝16；36－16＝20；…；设n表示自然数，试用关于n的等式表示出你所发现的规律：＿＿＿＿＿＿＿＿＿。
46、已知：
，
，
，…若
（a、b为正整数），则a＋b＝________．
47、下面是按照一定规律画出的一列“树型”图：
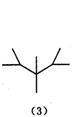
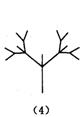
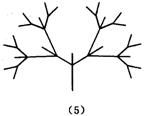
经观察可以发现：图(2)比图(1)多出2个“树枝”，图(3)比图(2)多出5个“树枝”，图(4)比图(3)多出10个“树枝”，照此规律，图(7)比图(6)多出 个“树枝”．
48、探究数字“黑洞”：“黑洞”原指非常奇怪的天体，它体积小，密度大，吸引力强，任何物体到了它那里都别想再“爬”出来．无独有偶，数字中也有类似的“黑洞”，满足某种条件的所有数，通过一种运算，都能被它“吸”进去，无一能逃脱它的魔掌．譬如：任意找一个3的倍数的数，先把这个数的每一个数位上的数字都立方，再相加，得到一个新数，然后把这个新数的每一个数位上的数字再立方、求和，…，重复运算下去，就能得到一个固定的数T＝ ，我们称它为数字“黑洞”．
T为何具有如此魔力？通过认真的观察、分析，你一定能发现它的奥秘！
三、（每小题5分，共15分）
49、请先观察下列算式，再填空：
32―12=81，52―32=8×2
（1）72―52=8× ；
（2）92―( )2=8×4；
（3）( )2―92=8×5；
（4）132―( )2=8× ；……
通过观察归纳，写出反映这种规律的一般结论： 。
50、有若干个数，第一个数记为a1，第二个数记为a2，第三个数记为a3，…，第n个数记为an，若a1=，从第2个数起，每个数都等于：1与它前面的那个数的差的倒数，试求a2，a3，a5，的值，并判断a2004，a2005的值，写出推理过程.
51、分解因式：(1)xy3―x3y (2) 2q(1－p)3+2(p－1)2
四、计算或化简(每小题6分，共18分)
52、计算
(1) 
(2) 
53、计算
(1)
(2)[
54、先化简，再求值：
(1)已知：a =－1，求（1+
）÷
的值.
(2) (
，其中a满足：a2+2a－1=0
五、(本题7分)
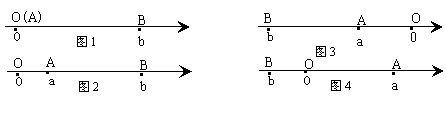55、（1）阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为∣AB∣。
当A、B两点中有一点在原点时，不妨设点A在原点，如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a-b∣；
当A、B两点都不在原点时，
如图2，点A、B都在原点的右边∣AB∣＝∣OB∣－∣OA∣＝∣b∣-∣a∣=b-a=∣a-b∣；
如图3，点A、B都在原点的左边，∣AB∣＝∣OB∣－∣OA∣＝∣b∣-∣a∣=－b-（-a）=∣a-b∣；
如图4，点A、B在原点的两边，∣AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣= a +（-b）=∣a-b∣；
（2）回答下列问题：
数轴上表示2和5的两点之间的距离是_________,数轴上表示－2和－5的两点之间的距离是_________,数轴上表示1和－3的两点之间的距离是_______；
数轴上表示x和－1的两点A和B之间的距离是___________，如果∣AB∣＝2，那么x为____；
（3）当代数式∣x+1∣+∣x-2∣取最小值时，相应的x的取值范围是_______________.