中考第一轮复习圆
第八单元
Ⅰ.梳理知识
1.圆的有关概念和基本性质
(1)圆的有关概念
(2)圆的基本性质
①对称性
②垂径定理及其逆定理
③圆心角、弦、弧之间的关系
④圆心角定理及其推论
2.直线与圆的位置关系
3.圆与圆的位置关系
4.弧长、扇形的面积、圆锥的侧面积计算公式
Ⅱ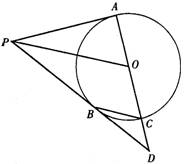
.典里例剖析
例1、如图．PA和PB分别与⊙O相切于A，B两点，作直径AC，并延长交PB于点D．连结OP，CB．
（1）求证：OP∥CB
（2）若PA＝12，DB：DC＝2：1，求⊙O的半径．
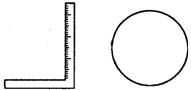
例2、现需测量一井盖（圆形）的直径，但只有一把角尺（尺的两边．互相垂直，一边有刻度，且两边长度都长于井盖半径）．请配合图形、文字说 明测量方案，写出测量的步骤（要求写出两种测量方案）．
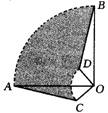例3、圆心角都是90°的扇形OAB与扇形OCD如图所示那样叠放在一起，连结AC、BD．
(1) 求证：△AOC≌△BOD；
(2) 若OA＝3cm，OC＝1cm，求阴影部分的面积．
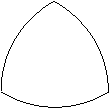例4、如图所示的曲边三角形可按下述方法作出：分别以正三角形的一个顶点为圆心，边长为半径，画弧使其经过另外两个顶点，然后檫去正三角形，三段圆弧所围成的图形就是一个曲边三角形。如果一个曲边三角形的周长为π，求这个曲边三角形的面积.
Ⅲ.同步测试
一、选择题(每小题3分，共30分)
1、在平面直角坐标系中，以点（2，1）为圆心，1为半径的圆，必与（ ）
A.x轴相交 B.y轴相交 C.x轴相切 D.y轴相切
2、如果两圆的半径分别为3和4，圆心距为7，那么这两个圆的位置关系是（ ）
A. 外切 B. 内切 C. 相交 D. 外离
3、圆锥的侧面展开图是一个半圆，则这个圆锥的母线长与底面半径的比是（ ）
A. 2∶1
B.2π∶1
C.
∶1
D.
∶1
4、如图，扇子的圆心角为x°，余下扇形的圆心角为y°，x与y的比通常按黄金比来设计，这样的扇子外形较美观。若取黄金比为0.6，则x为（ ）
A．216 B．135 C．120 D．108
5、如果圆锥的底面半径为3cm，母线长为4cm，那么它的侧面积等于（ ）
A.24πcm2 B.12πcm2 C.12cm2 D.6πcm2
6、一个圆锥的底面半径为
，母线长为6，则此圆锥侧面展开图的圆心角是（ B ）
A．180° B．150° C．120° D．90°
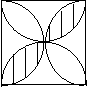
7、如图，正方形的变长为 a，以各边为直径在正方形内画半圆，则阴影部分的面积为（ ）
A.
a2-
a2 B.
a2-a2 C.a2-a2 D.πa2-a2
(第7题图) (第9题图) (第10题图)
8、小华想用一个圆心角为120°、半径为6cm的扇形做一个圆锥的侧面(接缝忽略不计)，则做成的圆锥底面半径为（ ）
A．4cm Ｂ．3cm Ｃ．2cm Ｄ．1cm
9、如图，A、B是⊙O上的两点，AC是⊙O的切线，∠B＝70°，则∠BAC等于（ ）．
A. 70° B. 35° C. 20° D. 10°
10、如图，PA、PB是⊙O的切线，切点分别为A、B，点C在⊙O上，如果∠P=50°, 那么∠ACB等于（ ）
A.40° B.50° C.65° D.130°
二、填空题(每小题3分，共24分)
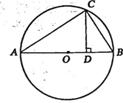
11、如图，AB为⊙O的直径，弦AC=4cm，BC=3cm，CD⊥AB，垂足为D，那么CD的长为____cm．
 |  | ||||
 | |||||
(第10题图) (第12题图) (第16题图)
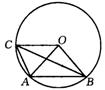
12、如图，A、B、C是⊙O上的三个点，当BC平分∠ABO时，能得出结论： （任写一个）．
13、已知⊙O1和⊙O2相外切，且圆心距为10cm，若⊙O1半径为3cm，则⊙O2的半径为__________cm.
14、一圆锥的母线长为6cm，它的侧面展开图的圆心角为120°，则这个圆锥的侧面积为________
.
15、已知⊙O1的半径为6cm，⊙O2的半径为2cm，O1O2=8cm，那么这两圆的位置关系是 .
16、如图，一把纸折扇完全打开后，外测两竹条AB和AC的夹角为120° ，AB长为25cm，贴纸部分的宽BD为17cm，则贴纸部分的面积为 cm(结果用π表示)
17、某学校需修建一个圆心角为60°，半径为12米的扇形投掷场地，则该扇形场地的面积约为_____________米2（结果保留π）.
18、在△ABC中，∠C=90°，AC=12，BC=5，现在AC为轴旋转一周得到一个圆锥。则该圆锥的表面积为 .
三、(每小题6分，共12分)
19、如图，五边形ABCDE是正五边形，曲线EA1B1C1D1……叫做“正五边形的渐开线”，其中EA1、A1B1、B1C1、C1D1、D1A2……的圆心依次按A、B、C、D、E循环，它们依次相连接，如果AB=1，求曲线EA1B1C1D1E1…D2E2…的长(结果保留π).
20、如图，一块直角三角板形状的木板于料，木工师傅要在此余料上锯出一块圆形的木版制作凳面，要想使锯出的凳面的面积最大
(1)请你试着用直尺和圆规画出此圆(要求尺规作图，保留作图痕迹，不写作法).
(2)若此R t△ABC的直角边分别为30cm和40cm，试求此圆凳面的面积.
四、(每小题8分，共32分)
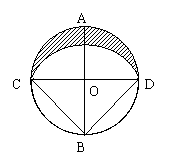
21、如图，已知⊙O的半径为R，直径AB⊥CD。以B为圆心，以BC为半径作弧CED，求弧CED与弧CAD围成的新月形ACED的面积S.
22、如图，点C在以AB为直径的半圆上，连结AC、BC，AB=10，tan∠BAC=
，求阴影部分的面积.
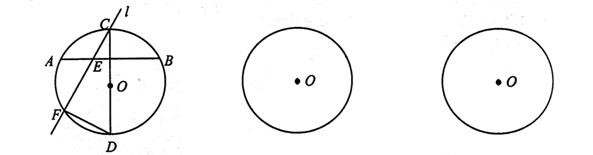
23、已知：如图，AB是⊙O的一条弦，点C为⌒AB的中点，CD是⊙O的直径，过C点的直线l交AB所在直线于点E，交⊙O于点F.
(1)判断图中∠CEB与∠FDC的数量关系，并写出结论；
(2)将直线l绕C点旋转(与CD不重合)，在旋转过程中，E点、F点的位置也随之变化，请你在下面两个备用图中分别画出l在不同位置时，使(1)的结论仍然成立的图形，标上相应字母，选其中一个图形给予证明.
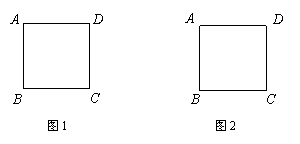
24、李大爷有一个边长为a的正方形鱼塘（图1），鱼塘四个角的顶点A、B、C、D上各有一棵大树.现在李大爷想把原来的鱼塘扩建成一个圆形或正方形鱼塘（原鱼塘周围的面积足够大），又不想把树挖掉（四棵大树要在新建鱼塘的边沿上）
（1）若按圆形设计，利用图1画出你所设计的圆形鱼塘示意图，并求出圆形鱼塘的面积；
（2）若按正方形设计，利用图2画出你所设计的正方形鱼塘示意图；
（3）你在（2）所设计的正方形鱼塘中，有无最大面积？为什么？
（4）李大爷想使新建鱼塘面积最大，你认为新建鱼塘的最大面积是多少？
 |