九年级数学上学期期考抽考
数 学 试 卷
一.填空题（每小题2分，共20分）
1. 等腰三角形底边长为7，一腰上的中线把其周长分成两部分的差为3，则腰长是________.
2. 若一个三角形的三边长均满足方程
，则此三角形的周长为
3. 若菱形的高是５ｃｍ ，且相邻两个内角度数的比是１：５，则它的面积是
4. 请写一个图像位于第二、四象限内的反比例函数的表达式：
5. 在阳光的照射下，直立于地面的竹竿的影子的变化情况是
6. 若关于x 的方程
有一根是0，则
1/19/2006
7.在南宁市有一个20000人的区域，随机调查3000人，其中450人，其中450人看中央电视台的晚间新闻，在该区域随便问一人，他（她）看中央电视台晚间新闻的概率是___________
8. 如图是置于水平地面上的一个球形储油罐，小敏想测量它的半
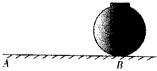径．在阳光下，他测得球的影子的最远点A到球罐与地面接触点B
的距离是10米(如示意图，AB＝10米)；同一时刻，他又测得竖直
立在地面上长为1米的竹竿的影子长为2米，那么，球的半径是___________米；
9. 某广场要做一个由若干盆花组成的形如正六边形的花坛,每条边(包括两个顶点)有n(n>1)盆花,设这个花坛边上的花盆的总数为S,请观察图中的规律:
按上规律推断,S与n的关系是_________________________。
10. 今年我区荔枝又喜获丰收. 目前市场价格稳定，荔枝种植户普遍获利. 据估计，今年全省荔枝总产量为50 000吨，销售收入为61 000万元. 已知“妃子笑”品种售价为1.5万元/吨，其它品种平均售价为0.8万元/吨，求“妃子笑”和其它品种的荔枝产量各多少吨. 如果设“妃子笑”荔枝产量为x吨，其它品种荔枝产量为y吨，那么可列出方程组为 .
二．选择题（每题3分，共24分）
1. 根据下图所示，对a、b、c三中物体的重量判断正确的是 ( ）
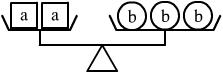
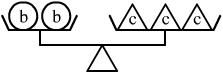
A. a<c B. a<b C. a>c D. b<c
2. 下列运算正确的是C
A．
B．
C．
D．
3. 一元二次方程
的根的情况为（ ）
A、有两个不相等的实数根 B、有两个相等的实数根
C、只有一个实数根 D、没有实数根
4．已知关于ｘ的一元二次方程ｘ２－2（Ｒ＋ｒ）ｘ＋ｄ２＝０没有实数根，其中Ｒ、ｒ分别为⊙Ｏ１、⊙Ｏ２的半径，ｄ为两圆的圆心距，则⊙Ｏ１与⊙Ｏ２的位置关系是（ ）
Ａ．外离 Ｂ．相交 Ｃ．外切 Ｄ．内切
5. 如图，小亮拿一张矩形纸图（1），沿虚线对折一次得图（2），下将对角两顶点重合折叠得图（3）。按图（4）沿折痕中点与重合顶点的连线剪开，得到三个图形，这三个图形分别是（ ）
A、都是等腰梯形 B、都是等边三角形
C、两个直角三角形，一个等腰三角形 D、两个直角三角形，一个等腰梯
6. 用不同颜色的马赛克片覆盖一个圆形的台面，估计150圆心角的扇形部分大约需要34片马赛克片。已知每箱装有125片马赛克片，那么应该购买_______箱马赛克片才能铺满整个台面。
A、5－6 B、6－7 C、7－8 D、8－9
7. 李大伯承包了一个果园，种植了100棵樱桃树，今年已进入收获期。收获时，从中任选并采摘了10棵树的樱桃，分别称得每棵树所产樱桃的质量如下表：
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 质量（千克） | 14 | 21 | 27 | 17 | 18 | 20 | 19 | 23 | 19 | 22 |
据调查，市场上今年樱桃的批发价格为每千克15元。用所学的统计知识估计今年此果园樱桃的总产量与按批发价格销售樱桃所得的总收入分别约为（ ）
A. 200千克，3000元 B. 1900千克，28500元
C. 2000千克，30000元 D. 1850千克，27750元
8. 在直角坐标系中，O为坐标原点，A(1，1)，在x轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P共有( A )
A.4个 B.3个 C.2个 D.1个
三．计算题（每题8分，共16分）
1.计算
2.解不等式组 
四．解答题（每题10分，共40分）
1. 南宁市是广西最大的罗非鱼养殖产区，被国家农业部列为罗非鱼养殖优势区域．某养
殖场计划下半年养殖无公害标准化罗非鱼和草鱼，要求这两个品种总产量
（吨）满
| 品种 | 单价（万元/吨） |
| 罗非鱼 | 0.45 |
| 草鱼 | 0.85 |
足：
，总产值为1000万元．
已知相关数据如右表所示．
求：该养殖场下半年罗非鱼的产量应控制在什么
范围？（产值＝产量
单价）
2.南宁市政府为了了解本市市民对首届中国－东盟博览会的总体印象，利用最新引进的
“计算机辅助电话访问系统”（简称CATI系统），采取电脑随机抽样的方式，对本市
年龄在16～65岁之间的居民，进行了300个电话抽样调查．并根据每个年龄段的抽查人数和该年龄段对博览会总体印象感到满意的人数绘制了下面的图（1）和图（2）（部分）
 | |||||
 | |||||
| |||||
| |
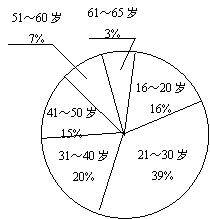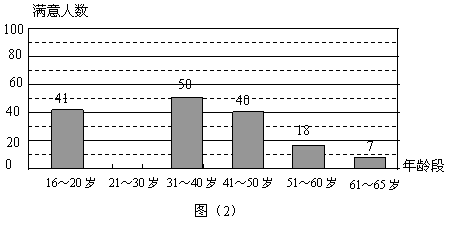（１）被抽查的居民中，人数最多的年龄段是 岁；
（２）已知被抽查的300人中有83%的人对博览会总体印象感到满意，请你求出21～30岁
年龄段的满意人数，并补全图12－2；
（３）比较21～30岁和41～50岁这两个年龄段对博览会总体印象满意率的高低（四
舍五入到1%）．
注：某年龄段的满意率＝该年龄段满意人数
该年龄段被抽查人数100％
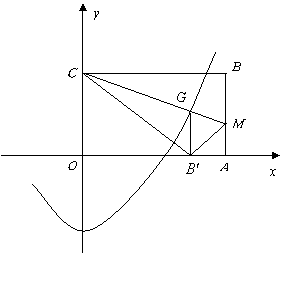
3. 
是一张放在平面直角坐标系中的矩形纸片，
为原点，点
在
轴上，点
在
轴上，
．
（１）
如图，在
上取一点
，使得
沿
翻折后，点
落在轴上，记作
点．求点的坐标；
（２）
求折痕所在直线的解析式；
（３）
作
交于点，若抛物线
过点，求抛物线的解析式，并判断以原点为圆心，
为半径的圆与抛物线除交点外，是否还有交点？若有，请直接写出交点的坐标．
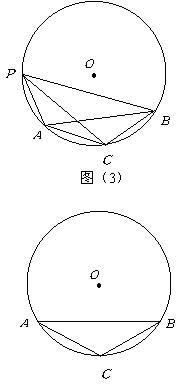
4．如图（3），点
是圆上的一个动点，弦
是
的平分线，
．
（１）
当
等于多少度时，四边形
有最大面积？最大面积是多少？
（２）
当等于多少度时，四边形是梯形？说明你的理由．
 |