九年级数学试卷

九年级数学试卷　　　

选择题（每题3分，共30分）

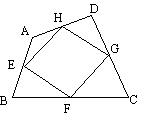
1、如图，E、F、G、H分别是四边形ABCD四条边的中点，要使四边形EFGH为矩形，四边形ABCD应具备的条件是（　　）.

（A）一组对边平行而另一组对边不平行　（B）对角线相等

（C）对角线互相垂直　　　　　　　　  （D）对角线互相平分

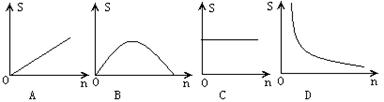
2、如图，两块完全重合的正方形纸片，如果上面的一块绕正方形的中心O左0°~90°的旋转，那么旋转时露出的△ABC的面积（S）随着旋转角度（n）的变化而变化，下面表示S与n关系的图象大致是（　）

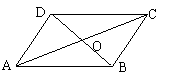
3、如图，□ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取值范围是（　）

A、1< m <11　  B、2< m <22　　C、10< m <12　　 D、5< m <6

4、如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_______.

5、已知关于x的方程x²－（a＋b)x＋ab－2＝0. x₁、x₂是此方程的两个实数根,现给出三个结论：

（1）　 x₁≠x₂　　　（2）　 x₁x₂＞a b 　　　 (3 ) x₁²＋x₂²＞a²＋b²　　

正确的有（　）个（A）1　　 (B)2　　　 (C) 3　　(D)　0

6、一个容量为50的样本,在整理频率分布时,将所有频率相加,其和是(　　　).

A.50　　　　　　　 B.0.02　　　　　　 C.0.1　　　　　　  D.1

7、已知一组数据5，15，75，45，25，75，45，35，45，35，那么40时这一组数据的（ ）

A．平均数但不是中位数　　　　　　 B.平均数也是中位数

C．众数　　　　　　　　　　　　　 D. 中位数但不是平均数

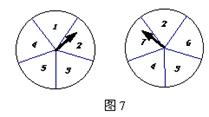
8、图7所示的两个圆盘中,指针落在每一个数上的机会均等,则两个指针同时落在偶数上的概率是（　）

A．　 B．　C．　D．

9、在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下（　 ）

（A）小明的影子比小强的影子长　　  （B）小明的影长比小强的影子短

（C）小明的影子和小强的影子一样长　（D）无法判断谁的影子长

10、.三角形两边长分别为3和6，第三边是方程的解，则这个三角形的周长是

 （A）11　（B）13　（C）11或13　（D）11和13

一、填空题（每题3分，共28分）

1、　已知数据x₁，x₂，…，x_n的平均数是，则一组新数据x₁+8,x₂+8,…,x_n+8的平均数是____.

2、  在直角三角形ABC中，∠C=90°，已知sinA=,则cosB=_______.

3、  二次函数y=x²-2x+1的对称轴方程是x=_______.

4、对甲、乙两台机床生产的零件进行抽样测量，其平均数、方差计算结果如下：机床甲：=10，=0.02；机床乙：=10，=0.06，由此可知：________（填甲或乙）机床性能好.

5、关于x的方程m²x²+(2m+3)x+1=0有两个乘积为1的实数根,方程x²+(2a+m)x+2a+1-m²=0有一个大于0且小于4的实数根,则a的整数值是_________.

6、　口袋中放有3只红球和11只黄球，这两种球除颜色外没有任何区别.随机从口袋中任取一只球，取到黄球的概率是_____.

7、.点P既在反比例函数的图像上，又在一次函数的图像上，则P点的坐标是___________.

8、.在△ABC中，∠A、∠B、∠C均为锐角，其对边分别为b、c,则下列结论一定成立的有（　　 ）个；

①;②S_△ABC=;③=;④.

A.1　　　　　　　　　 B.2　　　　　　　 C.3　　　　　　　　　 D.4

二、解答题

1、如图，□ABCD中，AE、CF分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是　　　 （只需写出一个即可，图中不能再添加别的“点”和“线”）.

2、已知方程的一个根是-5，求它的另一个根及的值.

3、在“深圳读书月”活动中，小华在书城买了一套科普读物，有上、中、下三册，要整齐的摆放在书架上，有哪几种摆法？其中恰好摆成“上、中、下”顺序的概率是多少？

4、如图10，一次函数的图象与反比例函数的图象交于M、N两点.

（1）求反比例函数和一次函数的解析式；

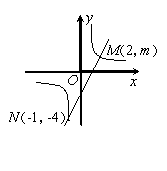（2）根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.

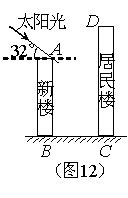5、某居民小区有一朝向为正南方向的居民楼（如图12），该居民楼的一楼是高6米的小区超市，超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.

（1）问超市以上的居民住房采光是否有影响，为什么？（5分）

（2）若要使超市采光不受影响，两楼应相距多少米？（4分）

（结果保留整数，参考数据：°≈，°≈，°≈）

6、已知抛物线y= x²+（2n-1）x+n²-1（n为常数）.

（1）当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；

（2）设A是（1）所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C.

①当BC =1时，求矩形ABCD的周长；②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由.

7、将正方形ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G（如图）.

（1）如果M为CD边的中点，求证：DE∶DM∶EM=3∶4∶5；

（2）如果M为CD边上的任意一点，设AB=2a，问△CMG的周长是否与点M的位置有关？若有关，请把△CMG的周长用含DM的长x的代数式表示；若无关，请说明理由.

8、如图，抛物线经过点A(1，0)，与y轴交于点B。

⑴求抛物线的解析式；

⑵P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，试求P点坐标。

9、某生活小区的居民筹集资金1600元，计划在一块上、下底分别为10m，20m的梯形空地上种植花木（如图10-1）

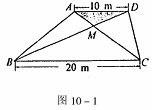（1）他们在△AMD和BMC地带上种植太阳花，单价为8元/m²，当△AMD地带种满花后（图10-1中阴影部分），共花了160元，请计算种满△BMC地带所需的费用.

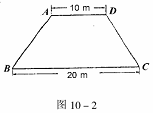（2）若其余地带要种的有玫瑰和茉莉花两种花木可供选择，单价分别为12元/m²和10元/m²，应选择种哪种花木，刚好用完所筹集的资金？（3）若梯形ABCD为等腰梯形，面积不变（如图10-2），请你设计一种花坛图案，即在梯形内找到一点P，使得△APB≌△DPC且S_△APD= S_△BPC，并说出你的理由.

10、目前国内最大跨径的钢管混凝土拱桥——永和大桥，是南宁市又一标志性建筑，其拱形图形为抛物线的一部分（如图9-1），在正常情况下，位于水面上的桥拱跨度为350米，拱高为85米.

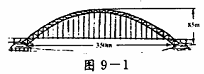（1）在所给的直角坐标系中（如图9-2），假设抛物线的表达式为y= ax²+b，请你根据上述数据求出a、b的值，并写出抛物线的表达式（不要求写自变量的取值范围，a、b的值保留两个有效数字）.

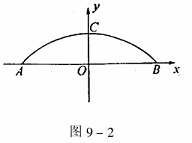
（2）七月份汛期将要来临，当邕江水位上涨后，位于水面上的桥拱跨度将会减小 .当水位上涨 4 m 时，位于水面上的桥拱跨度有多大？（结果保留整数）.