九年级数学中考模拟试卷三
一、填空题：(每题3分 共36分)
１、下列各式 ①
②
③ 
④
⑤ 
⑥
其中是一次函数的有（ ），是正比例函数的有（ ） （填序号）
2、
中，自变量的取值范围是（
）
3、已知点
其中
是一元二次方程
的两根，则点M的坐标为（
）
4、若一次函数
的图象经过原点且
随
的增大而减小，则
应满足的条件是（
）
5、函数
如果
，
则它的图象经过（
）象限，随的增大而（
）
6、在⊙O中，已知∠AOB=
则弦AB所对的圆周角是（
）
7、已知
是锐角，且
则的取值范围是（
）
8、已知
是方程
的一根，则
( )（
为锐角）
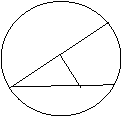
9、如图：∠BAC=
ADBCE为⊙O内接五边形，则∠D+∠E的度数为(
)
A
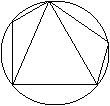10、如图，在⊙O中，
D
B
直径AB=10 弦AD=8 E O
P是弦AD上一个动点，
那么OP的取值范围是 A D
( ) B C P
（第9题） （第10题）
二、选择题（每题３分，共３０分）
11、四边形ABCD是⊙O的内接四边形，则∠A∠B∠C∠D的度数比依次是（ ）
（A）1:2:3:4 （B）6:7:8:9 （C）4:1:3:2 （D）14:3:1:12
12、已知∠A 是锐角，且
则有（
）
（A）
（B）
（C）
（D）
13、判断下列数量关系中，①正方形周长与它的一边长 ②圆周长和它的半径 ③圆的面积和它的周长 ④矩形面积一定时，长y与宽x ⑤买15斤梨售价25元，买x斤梨的售价y(元)与斤数x ⑥某人年龄与体重，其中是正比例函数关系的有（ ）
（A）①②④ （B）①②⑤ （C）①④⑤ （D）①③⑤
14、已知方程
有两个相等的实数根，则锐角
等于（
）
（A）
（B）
（C）
（D）以上都不对
15、若
为一次函数，则m的值为（ ）
（A）m=2或
（B）
且
（C）
（D）
16、点N在轴左侧，且到轴的距离为４，到轴距离为３的点N的坐标是（ ）
（A）
（B）
（C）或
（D）或
17、下列各命题中不是真命题的有（ ）
（A）相等的弧所对的弦相等 （B）相等的弦所对的弧相等
（C） 圆内接平行四边形是矩形（D） 圆内接梯形是等腰梯形
18、已知平面直角坐标系中，有三点
则△ABC的形状是（ ）
（A）等腰三角形 （B）直角三角形 （C）等边三角形 （D）等腰直角三角形
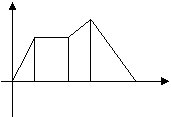
19、星期天晚饭后，小红从家里出去散步，右图描述了她散步过程中离家的距离s(m)与所用时间t(min)的函数关系，依据图象，下面的描述符合小红散步情景的是（ ）
(A) 从家出发到了一个公共阅报栏看了一会报就回家了
(B) 从家出发到了公共阅报栏，看了一会报后继续向前走了一段，然后回家了
(C) 从家出发一直散步（没有停留）然后回家了
(D) 从家出发散了一会步就找同学去了，１８分钟后开始返回
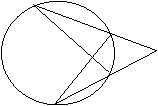
20、⊙O的弦AB、CD的延长线相交于P，若∠P
∠AMC
则∠ABC=（ ）
（A）
（B）
（C）
（D）
A
B
M P
(第19题) 4 10 15 18 (第20题) C D
三、解答题：（21、22、23各６分，24、25各８分）
21、国庆期间，几名教师包租一辆车前往合肥游览，面包车的租价为180元，出发时又增加两名教师，结果每一位教师比原来少分摊了３元车费，求参加旅游的教师共多少人？
22、已知一次函数的图象与
平行且过点
（１）求这个函数的解析式
（２）设此函数图象与轴、轴交点为A、B 求△AOB的面积
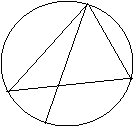23、已知AB是⊙O的直径，弦CD与AB相交于E，∠ADC= ∠ACD=求∠AEC的度数
A
O
D E C
B
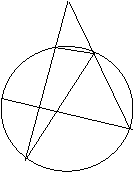24、已知：C为⊙O外一点过点C的两条直线分别交⊙O于E、D、F、B（如图），⊙O的直径AB⊥DE于H 求证：（１）∠CFE=∠DFB （2）
C
E F
A
O
B
D
25、某移动通讯公司开设了两种通讯业务“全球通”使用者先缴50元月租费，然后每通话１分钟再付话费0.4元，“快捷通”不缴月租费，每通话１分钟，付话费0.6元（均指市内通话）若一个月内通话分钟，两种方式的话费分别为
元与
元
（１）
写出与与之间的函数关系式
（２）一月内通话多少分钟，两种话费一样多？
（３）某人估计一个月内通话300分钟，选哪一种方式更合算些？
四、思考题：（１０分）
26、已知：函数
当
时
，此函数图象与轴、轴交点分别为A、B
（１）求
值，并求出点A与点B的坐标
（２）试问分别过△ABO的三个顶点中的一点，且把该三角形面积分成1:3两部分的直线
共有几条？并求出其中任意一条直线的解析式（每多写出一条直线的解析式可以加５分）（附加题总分不超过２０分）
答案
一、填空题：（每空3分，共计36分）
1、②④⑥ ④ 2、－3<x≤2 3、(3,－1)或(－1,3) 4、m>2且n=－3
5、一、三、四 增大 6、或
7、
8、
9、
10、3≤OP≤5
二、选择题（每题3分，共计30分）
DBBAC DBDBB
三、解答题：
21、解：设参加旅游的教师共人
依题意得： 
3分
解这个方程 
整理，得 
解得: 
5分
经检验： 是原方程的解，
但不合题意，舍去∴
答：参加旅游的教师共12人。 6分
22、解：（1）设所求的解析式为
由已知得
∴
1分
把代入得
∴
这个函数解析式为
3分
（2）∵
时
时
∴图象与轴、轴的交点为
5分
∴
6分
23、解：连结BD、BC
∵AB为⊙O直径∴∠ADB=∠ACB=
1分
∵∠ABC=∠ADC= ∠ABD=∠ACD= 3分
∴∠BAD==∠BCD ∴∠AEC=∠ ABC +∠BCD=
6分
24、证明：（1）连结DB ∵BDEF为⊙O内接四边形
∴∠CFE=∠EDB 1分
又∵直径AB⊥弦ED ∴弧BE=弧BD
∴∠EDB=∠DFB 3分
∴∠CFE=∠DFB 4分
（2）∵∠CFE=∠DFB ∠CEF=∠DBF
∴△CEF∽△DBF 6分
∴
8分
25、解（1）依题意
2分
（2）依题意
即 
解得
4分
∴通话250分钟话费一样多 5分
（3）当
时，
(元)
(元) 7分
∴选择全球通更合算些 8分
四、思考题
解（1）把 代入
中得
∴
2分
∴
当时
当时
即与轴、轴交点
4分
（2）直线共有六条（如图） 7分
①
设直线
交OB于点D，且OD:DB=1:3
∵OB=4 ∴OD=1∴D(0,1)
设的解析式为
把 D(0,1)代入得
解得
∴直线的解析式为
10分
②设直线
交OB于D，则点D(0,3)
把 D(0,3) 代入中
解得
∴直线的解析式为
15分
同法可求过点B交OA于点D两条直线的解析式为
: 
: 
20分
以上任写一条直线解析式均可