新课标(北师大版)中考数学第一轮复习测试卷
第十单元 三角形的认识与证明
一、选择题(每小题4分，共40分)
1、以下列各组线段长为边，能组成三角形的是（ B ）
A. 1cm，2cm，4cm B. 8cm，6cm，4cm
C. 12cm，5cm，6cm D. 2cm，3cm，6cm
2、等腰三角形的一个角是120°，那么另外两个角分别是（ B ）
A.15°、45° B.30°、30° C.40°、40° D.60°、60°
3、如图，在△ABC中，D、E分别是边AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为（ D ）
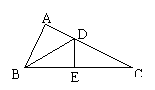A.15° B.20° C.25° D.30°
 |
(第3题图) (第4题图) (第5题图)
4、如图，已知MB=NB，∠MBA=∠NDC，下列条件不能判定△ABM≌△CDN的是（ C ）
A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN
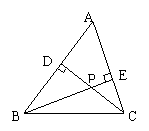
5、如图，在锐角△ABC中，CD、BE分别是AB、AC边上的高，且CD、BE交于一点P，若∠A=50°，则∠BPC的度数是（ B ）
A．150° B．130° C．120° D．100°
6、如果等腰三角形的底角为30°，腰长为6cm，那么这个三角形的面积为（ B ）
A.4.5cm2 B.9
cm2 C.18cm2 D.36cm2
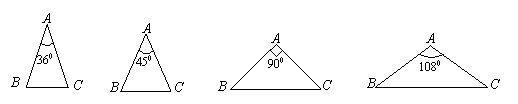7、如图，在下列三角形中，若AB＝AC，则能被一条直线分成两个小等腰三角形的是（ D ）
（1） （2） （3） （4）
A.（1）（2）（3） B. （1）（2）（4） C.（2）（3）（4） D. （1）（3）（4）
8、如图，在△ABC中，AB=AC，∠C=30°，AB⊥AD，AD=a，则BC的长为（ C ）
A.a
B.2a
C.3a D.4a
 | |||
 | |||
(第8题图) (第9题图) (第10题图)
9、如图，已知边长为5的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC边上的点D的位置，且
，则CE的长是（ D ）
A.10-15 B.10-5 C.5-5 D.20-10
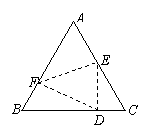
10、如图，CB、CD是钝角△AEC和锐角△ABC的中线，且AC=AB，给出下列结论：①AE=2AC；②CE=2CD；③∠ACD=∠BCE；④CB平分∠DCE。其中正确的有（ C ）
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分，共40分)
11、把一块周长为20cm的三角形铁片裁成四块形状、大小完全相同的小三角形铁片，则每块小铁片的周长为 10 cm.
12、已知：如图，△ABC中，BD平分∠ABC，且D为AC的中点，DE∥BC交AB于点E，若BC=4，则EB长为___2_____.
   | |||
 | |||
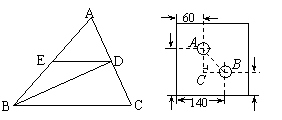(第12题图) (第13题图) (第14题图) (第15题图)
13、如图是一个外轮廓为矩形的机器零件平面示意图，根据图中标出尺寸（单位：mm）计算两圆孔中心A和B的距离为 100mm .
14、如图，在△RtABC中，∠B=90°，∠A=40°，AC的垂直平分线MN与AB交于D点，则∠BCD的度数是 10° .
15、如图，在△ABC中，BC=8，AD是BC边上的高，D为垂足，将△ABC折叠使点A与点D重合，则折痕EF的长为 4 .
三、(每小题8分，共16分)
16、正方形网格中，小格的顶点叫做格点。小华按下列要求做图：在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一条实线上；连结三个格点，使之构成直角三角形。小华在左边的正方形网格中作出了Rt△ABC，请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等.
 |  | ||
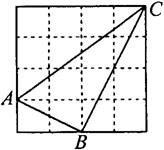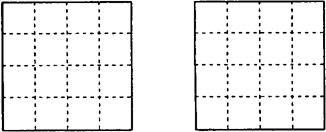略
17、如图，在△ABC中，∠C=90°。
（1）用圆规和直尺在AC上作一点P，使点P到A、B的距离相等（保留作图痕迹，不写作法和证明）。
（2）当满足（1）的点P到AB、BC的距离相等时，求∠A的度数。
(1)略 (2)∠A=30°
四、(每小题9分，共18分)
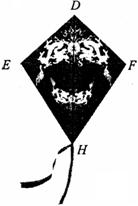
18、三月三，放风筝。如图是小明制作的风筝，它根据DE=DF，EH=FH，不用度量，就知道∠DEH=∠DFH。请你用所学知识给予证明.
略
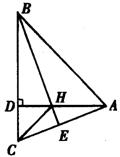19、如图，△BDA、△HDC都是等腰直角三角形，且D在BC上，BH的延长线与 AC交于点E，请你在图中找出一对全等三角形，并写出证明过程．
△ADC≌△BDH 证明略.
五、(每小题10分，共20分)
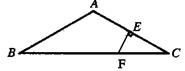20、如图，在△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F.
求证：BF=2CF.
证明略
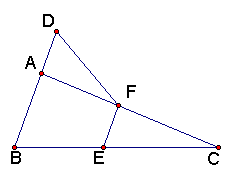21、如图，在△ABC中，∠BAC=90°，延长BA到点D，使AD=
AB，点E、F分别为BC、AC的中点.
(1)求证： DF=BE;
(2)过点A作AG∥BC，交DF于点G，求证：AG=DG.
(1)证明略 (2)证明略
六、(本题12分)
22、张老师在一次“探究性学习”课中，设计了如下数表：
| n | 2 | 3 | 4 | 5 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | … |
| b | 4 | 6 | 8 | 10 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(1)请你分别观察a、b、c与n之间 关系，并用含自然数n(n>1)的代数式表示.
a= ，b= ，c= .
(2)猜想：以a、b、c为边的三角形是否为直角三角形？并证明你的猜想.
(1)a=n2-1，b=2n，c=n2+1 (2)以a、b、c为边的三角形是直角三角形 理由略.
七、(本题12分)
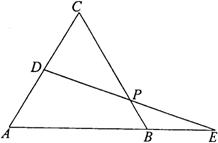23、已知：如图，正△ABC的边长为a，D为AC边上的一个点，延长AB至E，使BE=CD，连结DE，交BC于点F.
(1)求证：DP=PE；
(2)若D为AC的中点，求BP的长.
(1)证明略 (2)
a
八、(本题12分)
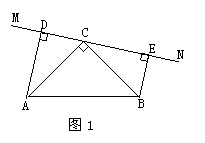
24、在△ABC中，∠ACB = 90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；
(2)当直线MN绕点C旋转到图2的位置时，求证：DE = AD-BE；
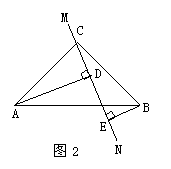
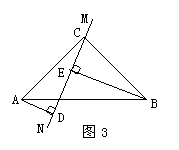(3)当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE 具有怎样的等量关系？请写出这个等量关系(不必证明).
 |
(1) ① ∵∠ACD=∠ACB=90°
∴∠CAD+∠ACD=90°
∴∠BCE+∠ACD=90°
∴∠CAD=∠BCE
∵AC=BC
∴△ADC≌△CEB
② ∵△ADC≌△CEB
∴CE=AD，CD=BE
∴DE=CE+CD=AD+BE
(2) ∵∠ADC=∠CEB=∠ACB=90°
∴∠ACD=∠CBE
又∵AC=BC
∴△ACD≌△CBE
∴CE=AD，CD=BE
∴DE=CE-CD=AD-BE
(3)当MN旋转到图3的位置时，AD、DE、BE所满足的等量关系是DE=BE-AD(或AD=BE-DE，BE=AD+DE等)
∵∠ADC=∠CEB=∠ACB=90°
∴∠ACD=∠CBE，
又∵AC=BC，
∴△ACD≌△CBE，
∴AD=CE，CD=BE，
∴DE=CD-CE=BE-AD.