第五单元 平面图形及其位置关系
三角形和四边形的认识与证明
Ⅰ.考点透视
一、平面图形及其位置关系
1.直线、射线与线段的区别与联系
2.角(角的两种定义、角的分类、角的度量以及余角、补角的概念和性质)
3.相交线与平行线
(1)相交线(对顶角的概念及其性质、垂线的概念及其性质)
(2)平行线(平行线的性质与判定)
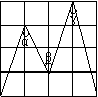
例1.如图，在正方形网格中，∠α、∠β、∠γ的大小关系是（ ）
A.α>β>γ B.α=β>γ C.α<β=γ D.α=β=γ
二、三角形的认识与证明
1.三角形(三角形的有关概念、三角形的分类、三角形中的重要线段以及三角形的有关性质)
2.全等三角形(全等三角形的性质与判定)
3.角平分线与线段的垂直平分线(定义、性质与判定)
例2.下列说法：①等边三角形有三条对称轴；②在△ABC中，若a2+b2≠c2，则△ABC不是直角三角形；③等腰三角形的一边长为4，另一边长9，则它的周长为17或22；④一个三角形中至少有两个锐角。其中正确的个数有（ ）
A、1个 B、2个 C、3个 D、4个
三、四边形的认识与证明
1.平行四边形(平行四边形的定义、性质与判定)
2.特殊的平行四边形
(1)矩形(定义、性质与判定)
(2)菱形(定义、性质与判定)
(3)正方形(定义、性质与判定)
3.梯形(等腰梯形的定义、性质与判定)
4.多边形(多边形的性质及其正多边形的特征)
例3.(1)正方形具有而菱形不一定具有的性质（ ）
A.四边都相等 B.对角线互相垂直且平分
C.对角线相等 D.对角线平分一组对角
(2)下列命题中假命题的是（ ）
A.对角线互相平分的四边形是平行四边形. B.两条对角线相等的四边形是矩形.
C.两条对角线互相垂直的矩形是正方形 D.两条对角线相等的菱形是正方形
(3)检查一个门框是矩形的方法是（ ）
A.测量两条对角线是否相等 B.测量有三个角是直角
C.测量两条对角线是否互相平分 D.测量两条对角线是否互相垂直
(4)顺次连接矩形各边中点所得的四边形是（ ）
A.矩形 B.菱形 C.梯形 D.正方形
(5)菱形的周长等于高的8倍，则其最大内角等于（ ）
A.60° B.90° C.120° D.150°
(6)矩形ABCD中，AB=8，BC=6，E、F是AC的三等分点，则△BEF的面积是（ ）
A.8 B.12 C.16 D.24
Ⅱ.中考演练
一、选择题(每小题4分，共40分)
1、如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC=70°，则∠BOD的度数等于（ ）
A.30° B.35° C.20° D.40°
 |
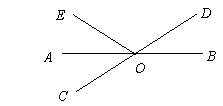(第1题图) (第3题图) (第5题图)
2、以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边，可以画出三角形的个数是（ ）
A.1 B.2个 C.3个 D.4个
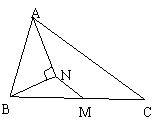
3、如图，在△ABC中，M为BC的中点，AN平分∠A，且AN⊥BN于点N，AB=10，AC=16，则MN等于（ ）
A.2 B.2.5 C.3 D.3.5
4、以下不能构成三角形三边长的数组是（ ）
A.（1，
，2） B.（，
，
） C.（3，4，5） D.（32，42，52）
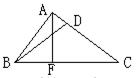
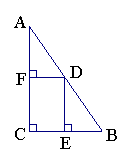
5、如图，在RtΔABC中，AF是斜边上的高线，且BD=DC=FC=1，则AC的长为（ ）
A.
B. C.
D.
6、顺次连结等腰梯形四边中点得到一个四边形，再顺次连结所得四边形四边的中点得到的图形是 ( )
A．等腰梯形 B．直角梯形 C．菱形 D．矩形
7、在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成平行四边形，又能拼成三角形和梯形的是
 |  |  |  |
A. B. C. D.
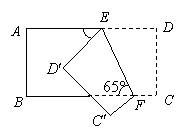
8、如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=65°，则∠AED′等于（ ）
A．50° B．55° C．60° D．65°
(第8题图) (第9题图) (第11题图)
9、如图，矩形ABCD中，AB=CD=x，AD=BC=y，把它折叠起来，使顶点A与C重合，则折痕PQ的长度为（ ）
A.
B.
C.
D.
10、如果要用正三角形和正方形两种图形进行密铺，那么至少需要（ ）
A.三个正三角形，两个正方形 B.两个正三角形，三个正方形
C.两个正三角形，两个正方形 D.三个正三角形，三个正方形
二、填空题(每小题4分，共40分)
11、如图，点D是Rt△ABC的斜边AB上的一点，DE⊥BC于E，DF⊥AC于F，若AF=15，BE=10，则四边形DECF的面积是 。
12、菱形的对角线长为6和8，则菱形的边长 ，面积是 .
13、矩形的对角线长为8，两对角线的夹角为60º，则矩形的两邻边分别长 和 .
14、已知：□ABCD中，对角线AC、BD相交于点O，添加适当的条件
（1）使它成为菱形.条件： .
（2）使它成为矩形.条件： .
（3）使它成为正方形.条件： .
15、四边形ABCD的两条对角线AC、BD互相垂直，ABCD是四边形ABCD的中点四边形。如果AC=8，BD=10，那么四边形ABCD的周长为 ，面积等于 .
三、(每小题8分，共16分)
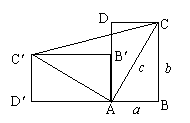16、一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法.如图，火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连结CC′，设AB=a，BC=b，AC=c，请利用四边形BCC′D′的面积证明勾股定理：a2+b2=c2.
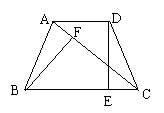17、等腰梯形ABCD中，AD∥BC，AB＝CD，DE⊥BC于E，AE＝BE，BF⊥AE于F，线段BF与图中的哪一条线段相等。先写出你的猜想，再加以证明。
猜想：BF＝ .
证明：
四、(每小题9分，共18分)
18、
如图△ABC中，∠B=2∠A, AB=2BC。
求证：∠C=90°.
19、已知：△ABC中AB=AC=a，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q.
(1)探究:当M位于BC的什么位置时，四边形AQMP是菱形？并说明你的理由.
(2)当△ABC满足什么条件菱形AQMP是正方形？
五、(每小题10分，共20分)
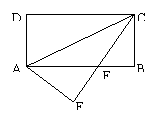20、在矩形ABCD中，AB=16，BC=8.将矩形沿AC折叠，点D落在点E处，且CE交AB于点F，求AF的长.
21、如图，AB、CD交于点E，AD=AE，CB=CE，F、G、H分别是DE、BE、AC的中点.
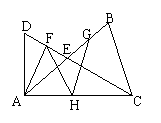求证：(1)AF⊥DE；
(2)FH=GH.
六、(本题满分12分)
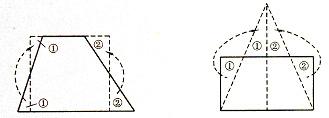
22、我们知道，一个平行四边形总可以剪开儿拼成一个矩形(如图1所示)，一个梯形可以剪开拼成一个矩形(如图2所示)，一个矩形可以剪开拼成一个三角形(如图3所示)。
 | |||
 | |||
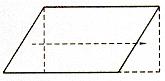图1 图2 图3
那么任意一个四边形呢？你也可以将它剪开而拼成各种各样的图形.
(1)请你仿上用图示的方法把它剪开而拼成平行四边形、矩形、三角形；
 | | |
(2)想想看，在这些剪拼过程中，都用到了图形的什么运动变换？
七、(本题满分12分)
23、据我国古代《周髀算经》记载，公元前1120年商高对周公说，将一根直尺折成一个直角，两端连结得到一个直角三角形，如果勾是三，股是四，那么弦就等于五。后人概括为“勾三、股四、弦五”.
(1)观察：3，4，5；5，12，13；7，24，25；……，发现这些勾股数的勾都是奇数，且从3起就没有间断过，计算
(9-1)，(9+1)与(25-1)，(25+1)，并根据你发现的规律，分别写出能表示7，24，25的股和弦的算式；(4分)
(2)根据(1)的规律，用n(n为奇数且n≥3)的代数式来表示所有这些勾股数的勾、股、弦，合情猜想他们之间二种相等关系并对其中一种猜想加以证明；(4分，除已发现的相等关系之外，你还有其他新的发现，并能正确证明，将酌情另加1~3分)
(3)继续观察4，3，5；6，8，10；，8，15，17；……，可以发现各组的第一个数都是偶数，且从4起也没有间断过。运用类似上述探索的方法，直接用m(m为偶数且m>4)的代数式来表示他们的股和弦.(4分)
八、(本题满分12分)
24、四边形是大家最熟悉的图形之一，我们已经发现了它的许多性质.只要善于观察、乐于探索，我们还会发现更多的结论.
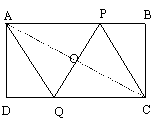
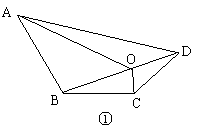
(1)四边形一条对角线上任意一点与另外两个顶点的连线，将四边形分成四个三角形(如图①)，其中相对的两对三角形的面积之积相等.你能证明这个结论吗？试试看.
已知：在四边形ABCD中，O是对角线BD上任意一点(如图①).
求证：S△OBC·S△OAD=S△OAB·S△OCD.
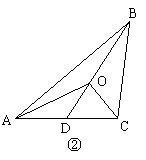(2)在三角形中（如图②），你能否归纳出类似的结论？若能，写出你猜想的结论，并证明：若不能，说明理由.