几何计算与证明

几何计算与证明

学校_______班别______姓名________学号________

一、　　　　 选择题：（每题3分，共15分）

1、　　　　  已知三角形两边a=3，b=7，第三边是c且a＜b＜c，则c的取值范围是（　　）

(A) 4＜c＜7　　(B) 7＜c＜10　　 (C)4＜c＜10　　(D)7＜c＜13

2、　　　　  若梯形中位线的长是高的2倍，面积是18cm²，则这个梯形的高等于（　  ）

(A)6cm　(B)6cm　 (C)3　 (D)3cm

3、　　　　  在Rt△ABC中，∠C=90°,若AB=2AC，则cosA等于（　）

(A) (B) (C) (D)

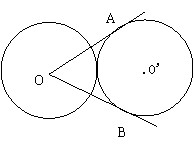4、已知：等圆⊙O和⊙O'外切，过O作⊙O'的两条切线OA、OB，A、B是切点，则∠AOB等于（　　　 ）

(A)30°  (B)45°　 (C)60°　 (D)90°

5、如果圆柱的母线长为6cm，侧面积是48πcm²，

那么这个圆柱的底面直径为（　 ）

(A)4cm　 (B)4πcm　 (C)8cm　 (D)8πcm

二、填空题：（每题4分，共24分）

1、三角形三内角的度数之比为1:2:3，最大边约长是8cm

则最小边的长是_______cm。

2、一个n边形的内角和等于外角和的3倍，则n=________。

3、若tanα+cotα=3，则tan²α+cot²α=_______。

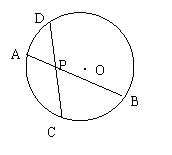4、　已知：如图，⊙O的弦AB平分弦CD，

AB=10，CD=8，且PA＜PB，则PB-PA=_______。

5、　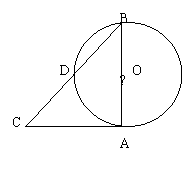　　　  如图，在△ABC中，∠BAC=90°，AB=AC=2，

以AB为直径的圆交BC于D，则图中阴影部分

面积为________。

6、　　　　  AB是斜靠在墙壁上的长梯，梯脚B距墙1.6米，

梯上点D距墙1.4米，BD长0.55米。

则梯子等于______米。

三、　　 解答题：（每题7分，共35分）

1、已知：如图，D、E是△ABC的边AB上的点，∠A=35°，∠C=85°，∠AED=60°，求证：AD·AB=AE·AC

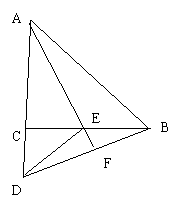2、如图：△ABC、△ECD都是等腰直角三形，且C在AD上，AE的延长线与BD交于F，请你在图中找出一对全等三角形，并写出证明它们全等的过程。

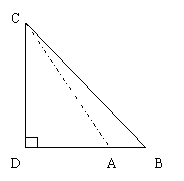3、如图：某学生在点A处，观测川河对岸水边有一点C，并测得∠CAD=45°，在距离A点30米的B处测得∠CBD=30°，求河宽CD。（结果可带根号）

4、　　　　  如图：已知直线MN与以AB为直径的半圆相切于点C，∠A=28°

（1）求∠ACM的度数。

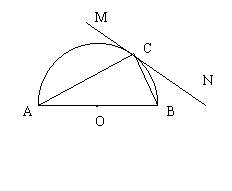（2）在MN上是否存在一点D，使AB·CD=AC·BC？为什么？

5、已知：⊙O₁和⊙O₂外切于A，⊙O₁、⊙O₂半径分别为5cm,7cm.

求外分切线AB的长。

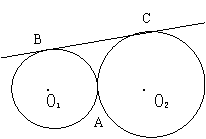四、综合题：

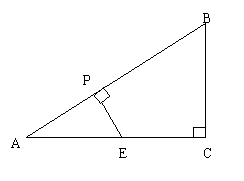1、如图，在△ABC中，∠C=90°，P为AB上一点，且点P与点A不重合，过点P作PE┴AB交AC边于E点，点E不与点C重合，若AB=10，AC=8，设AP长为X，四边形PECB的周长为Y。求Y与X之间的函数关系式。（12分）

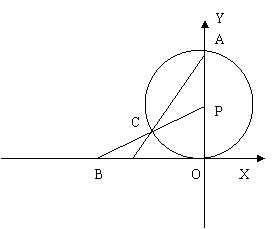
2、已知：如图，⊙P与X轴相切于坐标原点O，点（0，2）且⊙P与Y轴的交点，点B（-2，0）在X轴上，连结BP交⊙P于点C，连结AC并延度交X轴于点D。

（1）求线段BC的长。

（2）求直线AC的函数解析式。

（3）当点B在X轴上移动时，是否存在点，使△BOPVAOD？若存在，求出符合条件的点的坐标，若不存在，说明理由。（14分）