北师大版九年级（上）数学综合测试卷
班级_______姓名___________ 得分_________ .
一、选择题（每题3分，共30分）
1．如图1，在Rt△ACB中，∠ C = 90°，则 sin A = （ ）
A、
B、
C、
D、
2．在Rt△ACB中，∠ C = 90°，下列式子成立的是（ ）
A、a = c sin B B、a = b cos B C、c = a sin B D、a = b tan A .
3．在Rt△ACB中，若 tan A = 
，则锐角∠A = （ ）
A、30° B、45° C、60° D、不能确定.
4． 如图，
ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，
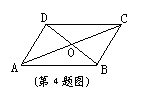那么m的取什范围是( )
A、1＜m＜11 B．2＜m＜22 C．10＜m＜12 D．5＜m＜6
5 。已知α为锐角且tan （90°－α）= ，则α= （ ）
A、30° B、45° C、60° D、不能确定.
6．在Rt△ACB中，∠ C = 90°，若sinA
= 
，则tanB =( )
A、
B、
C、
D、
.
7．在Rt△ABC中，∠C = 90°，AB = 10 ，BC = 8 ，则cos A = （ ）
A、
B、
C、
D、
.
8．掷一枚均匀的硬币两次，两次均为反面朝上的概率是（ ）
A、
B、
C、
D、
.
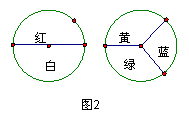
9．利用如图2的两个转盘进行“配紫色”的游戏，能配得紫色的概率是（ ） A、
B、 C、
D、
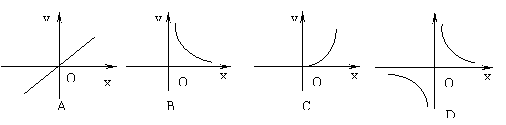10．甲、乙两地相距60km，则汽车由甲地行驶到乙地所用时间y（小时）与行驶速度x（千米/时）之间的函数图像大致是（ ）
二、填空题（每题3分，共15分）
11、方程 x
－2x = 0 的两根为___________.
12、 若反比例函数 y = 
的图象经过点（－1，2），则 k = _____________.
13、正方形的对角线长为2，则它的面积为___________.
14．三视图都相同的几何体有_________________________(至少写出两个).
15．为了估计池塘里有多少条鱼，从池塘里捕捞了100条鱼做上标记，然后放回池塘里，经过一段时间后，当有标记的鱼完全混合后，再捕捞200条，若其中有标记的鱼有10条，则估计池塘里有鱼________________条 .
三、解答题：
16．计算：
（本题7分）
17．计算：
（本题7分）
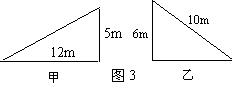18．如图3表示甲、乙两个自动扶梯，哪个自动扶梯比较陡？说明理由. （本题8分）
19．已知一次函数 y = kx + k 的图象与反比例函数 y = 
的图象在第一象限交于点
B（4，n ），求k、n的值 . （本题9分）
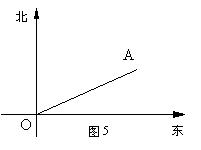
20．如图5，灯塔A周围1000米水域内有暗礁，一舰艇由西向东航行，在O处测得灯塔A在北偏东74°方向上，这时O、A相距4200米，如果不改变方向，此舰艇是否有触礁的危险？
（供参考数据：sin74°=0.96,cos74°=0.28,tan74°=3.49）（本题9分）
 |
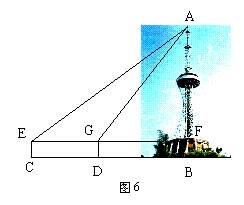21．如图6，在测量塔高AB时选择与塔底在同一水平面的同一直线上的C、D两点，用测角仪测得塔顶A 的仰角分别是30°和60°，已知测角仪高CE =
1.5米，CD = 30米，求塔高AB（答案保留根号） . （本题9分）
22．（本题8分）为响应承办“绿色奥运”的号召，某中学初三、2班计划组织部分同学义务植树180棵，由于同学们参与的积极性很高，实际参加植树活动的人数比原计划增加了50%，结果每人比原计划少栽了2棵树，问实际有多少人参加了这次植树活动？
23．（本题8分）某中学七年级有6个班，要从中选出2个班代表学校参加某项活动，七（1）班必须参加，另外再从七（2）至七（6）班选出1个班．七（4）班有学生建议用如下的方法：从装有编号为1、2、3的三个白球 袋中摸出1个球，再从装有编号为1、2、3的三个红球 袋中摸出1个球（两袋中球的大小、形状与质量完全一样），摸出的两个球上的数字和是几，就选几班，你人为这种方法公平吗？请说明理由．
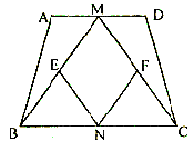
24．（本题10分）如图，在等腰梯形ABCD中，AD//BC，M、N分别为AD、BC的中点，E、F分别是BM、CM的中点。
（1）求证：
；
（2）四边形MENF是什么图形？请证明你的结论；
（3）若四边形MENF是正方形，则梯形的高与底边BC有何数量关系？并请说明理由。
