九年级期末考试试卷（北师大版）
试题均精选两年课改实验区中考题
一、潜心填空（每小题3分，共30分）
1.方程
的两个根是
。
2.已知方程
的一个根为
则加一根是
；k=
.
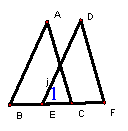
3.如图案，点E,C在BF上，∠1=∠B，EF=BC要证明△DEF≌△ABC，若根据“SAS”，需要补充条件；
。若根据“ASA”需要补充的条件： 。
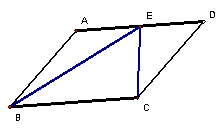
4.如图所示平行四边形ABCD中，AD=2AB，E为AD的中点，则∠BEC= 。
5.四边形ABCD的两条对角线相交于点O，AO=BO=CO=DO时，则四边形是 。
6.矩形ABCD中，对角线AC、BD交于O，若∠DOC=60°，BD=10cm，则AB= 。
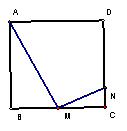
7.如图所示正方形ABCD中，M是BC中点，AM⊥MN交CD于N点，则CN= AB。
8.小明去商店准备买一条毛巾和一个浴花，恰好商店仅剩4条毛巾且颜色分别是白、黄、蓝。粉和2个浴花且颜色分别是蓝和粉，小明对营业员说：“我想买一样颜色的毛巾和浴花，”如果营业员随机抽取毛巾和浴花，那么抽到一样颜色的毛巾和浴花的概率是 。
9.小明和他的同桌在太阳光下行走，小明身高1.75m，他的影长是2.0m，小明的同桌比他矮5cm，此刻他的影子是 。
10.反比例函数
的图像上有一点P（m，n），其坐标是关于t的一元二次方程
两根，且P到原点的距离为
，则该反比例函数的解析式为
。
二、细心选择（每小题3分，共27分）
11等腰△ABC中，一腰AB的垂直平分线交另一腰AC于D，若AB=12，△DBC周长为20，则底边BC的长为
A.6 B.8 C.12 D.14
12.已知数菱形的周长为100cm，一条对角线为14cm，则它的面积是（ ）
A.168㎝2 B.336cm2 C.672cm2 D.84cm2
 | |||
 | |||
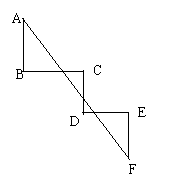
13.如图已知∠B=∠C=∠D=∠E=90°，且AB=CD=3，BC=4,DE=EF=2则A、F两点间的距离是
A.14 B.
C.10 D.
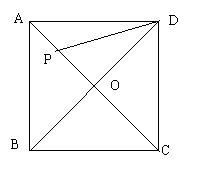
14.如图，正方形ABCD的两条对角线交于O点，在AO上取一点P，使∠OPD=60°，那么
=
A.
B.
C.
D.
15.某乡粮食总产量为100t，设该乡平均每人占有粮食为yt，人口数为yt，则y与x之间的函数关系的图像应为
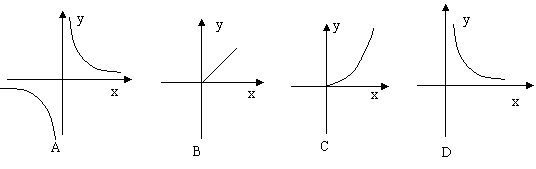
16.随意掷两个均匀的骰子，朝上面的点数之和是13的概率是
A.
B.1 C.
D.0
17.某厂今年3月的产值为50万元，5月上升到72万元，这两个月平均每月增长的百分率是多少？若设平均每月增长的百分率为x，则列出方程是（ ）
A.50（1+x）=72 B.
C.50（1+x）×2=72 D.
50
18.已知反比例函数
的图像上有两点A
，B
，且
，那么下列结论正确的是（ ）
A.
B.
C.
D.
与
之间的大小关系还能确定
19.已知一次函数
的图像经过第一、二、四象限，则反比例函数
的图像在（ ）
A.第一、二象限 B.第三、四象限 C。第一三象限 D。第二、四象限
三。耐心计算（8分）
20。解下列方程
（1）
（2）
四。巧妙设计（每题7分，共计14分）
21.画出下列几何体的三视图
 | |||
 | |||
22.（2004.贵阳）由一些大小相同的小正方体组成简单的几何体的主视图和俯视图（如图
（1）请你画出这个几何体的一种左视图。
（2）若组成这个几何体的小正方体的块数为n，求n的最大值与最小值。
| 主视图 | 俯视图 | |||||
23。快速解答（每题7分，共21分）
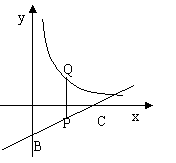（2004。新疆）如图所示，点P在经过点B（0，－2），C(4,0)的直线上，且纵坐标为－1，点Q在
的图像上，若PQ∥y轴。求点Q的坐标。
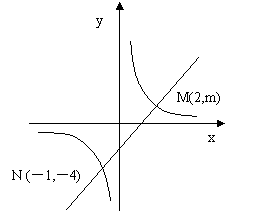
24.（2004.贵州）如图所示，一次函数的图像与反比例函数的图像交于M、N两点。
（1）求反比例函数和一次函数的解析式
（2）根据图像写出使反比例函数的值大于一次函数的值的x的取值范围
 |
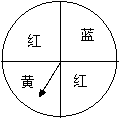
25.如图是“配紫色”游戏的两个转盘，你能用列表的方法求出配成紫色的概率吗？
 |
六、体验探究（每题10分共计20分）
26。（2004.湖北武汉）某公路上一路段维修工程准备对外招标，现有甲、乙两个工程队竞标，竞标材料上显示，若由两队合做，6天可以完工，共需工程费用10200元；若单独完成此项工程，甲队比乙队少用5天，但甲队每天的工程费用比乙队多300元，工程指挥部决定从这两个队中选一个队单独完成此项工程，若从节省资金的角度考虑，应该选择哪个工程队？为什么？
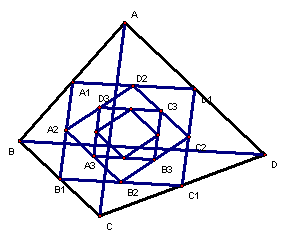
27.（2004.贵阳）如图所示，四边形ABCD中AC=6,BD=8且AC⊥BD，顺次连结四边形ABCD]各边中点，得到四边形
;再顺次连结四边形各边中点，得到四边形
……如此进行下去得到四边形
。
（1）证明；四边形是矩形
（2）写出四边和四边形的面积
（3）写出四边形的周长
（4）求四边
R的周长。