九年级上反比例函数同步训练1

九年级上反比例函数同步训练1　　　　　　　　　  姓名：_________

一．判断题

1．如果是的反比例函数，那么当x增大时，就减小　　　　　　　　　　　 （　　）

2．当与y乘积一定时，就是的反比例函数，也是的反比例函数　　　　  （　　）

3．如果一个函数不是正比例函数，就是反比例函数　　　　　　　　　　　　　　 （　　）

4．与成反比例时与并不成反比例　　　　　 　　　　　　　　　　　　 （　　）

5．与成反比例时，与也成反比例　　　　　　　　　　　　　　　　　  （　　）

6．已知与成反比例，又知当时，，则与的函数关系式是　 （　　）

二．填空题

1． (k≠0)叫__________函数.，的取值范围是__________；

2．已知三角形的面积是定值S，则三角形的高h与底a的函数关系式是h =__________,这时h是a的__________；

3．如果与成反比例，z与成正比例，则z与成____　　　　 ______；

4．如果函数是反比例函数，那么k=________，此函数的解析式是____　 ____；

三．辨析题

（1）兄弟二人分吃一碗饺子，每人吃饺子的个数如下表：

兄（y）	29	28	27	26	25	24	23	22	……	3	2	1
	——……→逐渐减少
弟（x）	1	2	3	4	5	6	7	8	……	27	28	29
	——……→逐渐增多

①写出兄吃饺子数与弟吃饺子数x之间的函数关系式（不要求写的取值范围）.

②虽然当弟吃的饺子个数增多时，兄吃的饺子数()在减少，但与x是成反例吗？

（2）水池中有水若干吨，若单开一个出水口，水流速v与全池水放光所用时t如下表：

用时t（小时）	10	5			2		1
	——……→逐渐减少
出水速度乙（吨/小时）	1	2	3	4	5	8	10
	——……→逐渐增大

①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系.

②这是一个反比例函数吗？

③与（1）的结论相比，可见并非反比例函数有可能“函数值随自变量增大而减小”，反之，所有的反比例函数都是“函数值随自变量的增大而减小吗？这个问题，你可以提前探索、尝试，也可以预习下一课时”反比例函数的图象和性质，也可以等到下一节课我们共同解决.

四．解答题：

1．已知一次函数和反比例函数（≠0）

（1）满足什么条件时这两个函数在同一坐标系xoy中图象有两个公共交点。

（2）设（1）中的两个公共点为A，B，则∠AOB是锐角还是钝角。

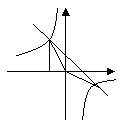2．如图，Rt_△ABO的顶点A是双曲线与直线在第二象限的交点，AB⊥轴于B且S_△ABO=

（1）求这两个函数的解析式

（2）求直线与双曲线的两个交点A，C的坐标和△AOC的面积。

九年级上反比例函数同步训练2　　　　　　　　　  　　 姓名：_________

一．填空题：

1．已知反比例函数，当时，其图象的两个分支在第一、三象限内；

当时，其图象在每个象限内随的增大而增大；

2．若直线和双曲线在同一坐标系内的图象无交点，则 、的关系是_________；

3． 若反比例函数的图象位于一、三象限内，正比例函数过二、四象限，则的整数值是________；

4．反比例函数的图象经过点P（，），且为是一元二次方程的两根，那么点P的坐标是________　　　_，到原点的距离为_________；

5．反比例函数的图象上有一点P（，），其坐标是关于t的一元二次方程的两个根，且点P到原点的距离为，则该反比例函数解析式为___　　 __　

二．选择题：

6．如果函数为反比例函数，则的值是　　　　　　　　　　　　　　　 （　　）

A　　　　　　B　　　 　　　 C　　　 　　　 D　　　　

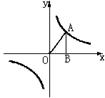
7．如图，A为反比例函数图象上一点，AB轴与点B，若，则为（　　）

A　　　 　　　B　　　

C　　　 　　　D　　　无法确定

8．若与成反比例，则与的函数关系式是　 （　　）

A.　　 正比例　　　B.　　反比例　　 C.　　一次函数　 　D.　　 二次函数

9．函数的图象经过（，，则函数的图象是　  （　　）

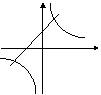
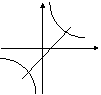
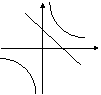
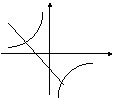10．在同一坐标系中，函数和的图像大致是　　　　　　　　　  （　　）

A　　　　　　　 B　　　　　　　　 C　　　　　　　　  　D

11．已知反比例函数的图像上有两点A(，)，B(，)，且，则的值是　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　  ）

A　　　正数　　 B　　　 负数　　 C　　 　非正数　　 D　　 不能确定

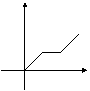
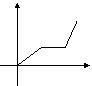
12．李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，结果准时到校。在课堂上，李老师请学生画出自行车行进路程s千米与行进时间t的函数图像的示意图，同学们画出的示意图如下，你认为正确的是　　　　　　　　　　　　　　　　　　　　　　　  （　　）

　　　　 A　　　　　　　 B　　　　　　　　  C　　　　　　　　　  D

三．解答题：

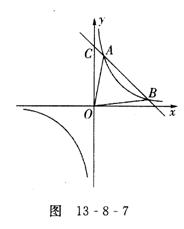
如图13－8－7已知一次函数和反比例函数

图象在第一象限内有两个不同的公共点A、B．

（1）求实数的取值范围；

（2）若ΔAOB的面积S＝24，求的值．

九年级上反比例函数同步训练3　　　　　　　　　　　　  姓名：_________

一．选择题：　

1、当＞0,＜0时，反比例函数的图象在　　　　　　　　　　　　　　　 （　　 ）（A）　　第一象限　 （B）　 第二象限　（C）　 第三象限　 （D）　 第四象限

2、下列函数中，是反比例函数的为　　　　　　　　　　　　　　　　　　　 （　　 ）

（A）  　 （B）　 　（C）　　　（D） 

3、若函数的图象过点（3，-7），那么它一定还经过点　　　　　　　　 （　　 ）

（A）　 （3，7）　 （B）　 （-3，-7） （C）　 （-3，7）　（D）　 （2，-7）

4、若反比例函数的图象位于第二、四象限，则的值是　　（　　 ）（A）　　　0　　　 （B）　　 0或1　　（C）　 0或2　　　（D）　　4

5、点A、C是反比例函数（k＞0）的图象上两点，AB⊥轴于B，CD⊥轴于D。记Rt△AOB和Rt△COD的面积分别为S₁、S₂，则　　　　　　　　　　　　　　　  （　　 ）

（A）　 S₁＞S₂（B）　　S₁＜S₂ （C）　　 S₁ = S₂（D）　不能确定

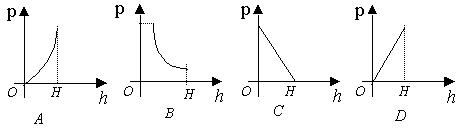6、已知圆柱的侧面积是100cm²，若圆柱底面半径为r（cm²），高线长为h（cm），则h关于r的函数的图象大致是　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　 ）

 

 

 

 

二、填空题：

1、为何值时，是反比例函数，即=　　　　　  ；

2、已知函数的图象有两个交点，其中一个交点的横坐标为1，则两个函数图象的交点坐标是　　　　　 ；

3、已知反比例函数图象与直线和的图象过同一点，则当＞0时，这个反比例函数值随的增大而　　　　 （填增大或减小）；

4、已知函数，当时，，则函数的解析式是　　　　　　 ；

5、在函数（为常数）的图象上有三个点（-2，），(-1，)，（，），函数值，，的大小为　 　　　　　；

6、如图，面积为3的矩形OABC的一个顶点B在反比例函数

的图象上，另三点在坐标轴上，则=　　　　　  .

7、反比例函数与一次函数的图象有一个交点是（-2，1），则它们的另一个交点的坐标是　　　　　　 .

三、解答题：

1、已知与成反比例，与成正比例，并且当=3时，=5，当=1时，=-1；求与之间的函数关系式.

 

 

2、　2、 如图，矩形ABCD，AB = 3，AD = 4，以AD为直径作半圆，为BC上一动点，可与B，C重合，交半圆于，设，求出关于自变量的函数关系式，并求出自变量的取值范围.

 

 

 

 

 

 

 

 

九年级上反比例函数同步训练4　　　　　　　　　　　　 姓名：_________

一．选择题：　

1．下列函数中，反比例函数是　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A　  　 B　　 　　C　　 　　　D　　

2．已知反比例函数的图像经过点（，），则它的图像一定也经过　　　　　　  （　　）

A　  (－,－)　  B　　 (,－)　　　C　　(－，)　　 D　　（0，0）

3．如果反比例函数的图像经过点（－3，－4），那么函数的图像应在　　　　（　　）

A　第一、三象限　 B　 第一、二象限 　 C　 第二、四象限　 D　 第三、四象限

4．若与－3成反比例，与成正比例，则是的　　　　　　　　　　　　 （　　）

A　 正比例函数　　B　　反比例函数　　 C　　 一次函数　　　D　　不能确定

5．若反比例函数的图像在第二、四象限，则的值是　　　　　 （　　）

A　　 －1或1　　 B　小于 的任意实数　C　　　 －1　　 　Ｄ　 不能确定

6．函数的图象经过点（－4，6），则下列各点中在图象上的是　　　　（　　）

A　  （3，8）　　 　B　　（3，－8）　　　C　 （－8，－3）　　D　（－4，－6）

7．正比例函数和反比例函数在同一坐标系内的图象为　　　　　　　 （　　）

　　　 A　　　　　　　　　　　　　　　　 B　　　　　　　　　　　　　　　 　C　　　　　　　　　　　　　　 D

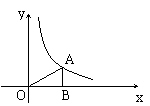8．如图，A为反比例函数图象上一点，AB垂直轴于B点，若

S_△AOB＝3，则的值为　　　　　　　　　　　　　　　　　　　　　　　  　　 （　　）

A、　6　 　B、　 3　　 　C、　　　 D、　 不能确定　　

9．如果与成反比例关系，与成正比例关系，则与成　　　　　　　　  （　　）

A．　正比例关系　B　 反比例关系　 C．　 一次函数关系　 D．　不同于以上答案

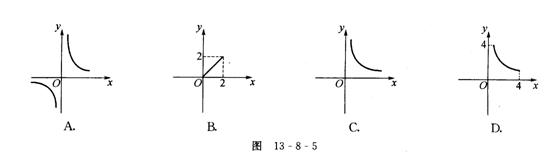10．如图13－8－5，面积为2的ΔABC，一边长为，这边上的高为，则与的变化规律用图象表示大致是 （　　）

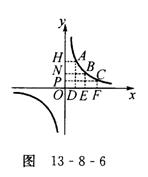11．如图13－8－6所示，A（，）、B（，）、C（，）是函数的图象在第一象限分支上的三个点，且＜＜，过A、B、C三点分别作坐标轴的垂线，得矩形ADOH、BEON、CFOP，它们的面积分别为S₁、S₂、S₃，则下列结论中正确的是　（　　）

A．　　　  S₁<S₂<S₃　　　　　　  B． S₃ <S₂< S₁

C．　S₂< S₃< S₁  D． S₁=S₂=S₃

二、解答题 ：

已知：反比例函数和一次函数，其中一次函数的图像经过点（，5）.

（1）　试求反比例函数的解析式；

（2）　　　　　　　　  若点A在第一象限，且同时在上述两函数的图像上，求A点的坐标；

九年级上反比例函数同步训练5　　　　　　　　　　　  姓名：_________

一．填空题

1．已知反比例函数，当时，其图象的两个分支在第一、三象限内；当时，其图象在每个象限内随的增大而增大；

2．反比例函数的图象经过点P（，），且、为是一元二次方程的两根，那么，点P的坐标是_________，到原点的距离为_________；

3．若点A(7，)、B(5，)在双曲线上，则和的大小关系为_________；

4．点 A（，）、B(, )均在反比例函数的图象上，若 ＜0，则 _____；

二．选择题：

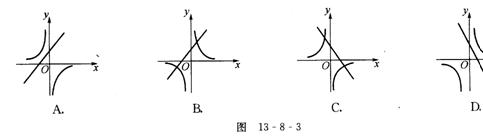5． 下列各图(如图13－8－3)已知一次函数，随的增大而减小，且，反比例函数中，与 值相等，则它们在同一坐标系中图象可能是　　　 （　　）

　　

6．如图 13－8－4，A、C是函数的图象上的任意两点，

过A作x轴的垂线，垂足为B，过C作y轴的垂线，垂

足为D，记RtΔAOB的面积为S₁，RtΔCOD的面积为S₂则　（　　）

A．　  S₁ ＞S₂　　　　　　  B． S₁ <S₂　

C． S₁=S₂　　　　　　　　D． S₁与S₂的大小关系不能确定

7．若矩形的面积为，则它的长与宽之间的函数关系用图象表示大致（　　）

A　　　　　　 　　　　 　 B　　　　　　　　　　 　　 　 C　　　　　　　　　　　　　　　　　 D

8．在同一直角坐标平面内，如果直线与双曲线没有交点，那么和的关系一定是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　　）

A　 <0，>0　　　　B　　>0，<0　　　C　 、同号 　D　 、异号

9．已知变量与成反比例，当时，；那么当时，的值是　　　 （ 　　）

A　　　　 6　　　　B　 　　―6　　　　 C　 　　　 9 　　　 D　　　―9

10．当路程一定时，速度与时间之间的函数关系是　　　　　　　　　　　　 （　　）

A　 　正比例函数　　B　　 反比例函数　　C　 　 一次函数　 　D　 　二次函数

三．解答题：

已知反比例函数和一次函数的图象都经过点，

⑴ 求点P的坐标和这个一次函数的解析式；

⑵ 若点M(，)和点N (，)都在这个一次函数的图象上．试通过计算或利用一次函数的性质，说明大于

九年级上反比例函数同步训练6　　　　　　　　　　　  姓名：_________

一．解答题：

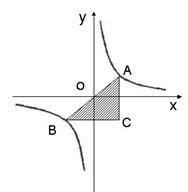
1．如图：A，B是函数的图象上关于原点O对称的任意两点。AC平行于轴，BC平行于轴，求△ABC的面积。

2．已知□ABCD中，AB = 4，AD = 2，E是AB边上的一动点，设AE=，DE延长线交CB的延长线于F，设CF =，求与之间的函数关系。

　　　　　　　　　　　　　　　　　　　　　　　　 

 3．如图，已知一次函数的图象与反比例函数y=的图象交于A，B两点，且A点的横坐标与B点的纵坐标都是；

（1）　　　 一次函数的解析式

（2）　　　 △AOB的面积。

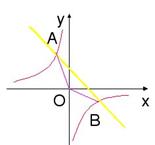
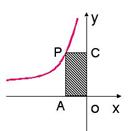
4．如图：P是反比例函数图象上的一点，由P分别向轴和轴引垂线，阴影部分面积为，求函数的表达式。

5．点A是双曲线与直线在第二象限的交点，AB垂直轴于点B，且S_△ABO=；（1）求两个函数的表达式

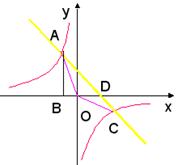（2）求直线与双曲线的交点坐标和△AOC的面积。