![]() 初中数学毕业升学考试试卷(一)
初中数学毕业升学考试试卷(一)
 一、选择题(本大题共8小题,每小题3分,共24分)
一、选择题(本大题共8小题,每小题3分,共24分)
1、下列各数中,小于零的数是( )
A、-![]() B、7-1 C、-(-7) D、(-7)-2
B、7-1 C、-(-7) D、(-7)-2
2、化简1+![]() 的结果是(
)
的结果是(
)
A、-![]() B、2-
B、2-![]() C、
C、![]() D、2+
D、2+![]()
3、在下列四个命题中,真命题的是( )
A、方程5x2=x只有一个实数根 B、方程2x2+3x-2=0没有实数根
C、方程-![]() =x没有实数根 D、方程x2=8有两个相等的实数根
=x没有实数根 D、方程x2=8有两个相等的实数根
 4、△ABC中,∠C=90°, tanA=
4、△ABC中,∠C=90°, tanA=![]() ,∠B等于( )
,∠B等于( )
A、30° B、45° C、60° D、90°
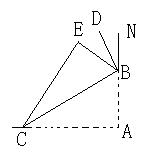
5、如图所示,把书页的一角斜折过去,设A点落在E处,BC为折痕,BD是∠EBN的平分线,则∠CBD是( )
A、锐角 B、直角 C、钝角 D、不能确定大小或范围的角
6、下列函数中,自变量取值范围是1<x≤2d的函数解析式是( )
A、y=![]() B、y=
B、y=![]() C、y=
C、y=![]() D、y=
D、y=![]()
7、两条对角线互相垂直且相等的四边形是( )
A、等腰梯形 B、菱形 C、矩形 D、形状不确定的四边形
8、全国青年京剧大奖赛,共有七位武旦演员进入决赛。决赛中,位武旦演员得分各不相同。某武旦想知道自己是否进入了前三名,她除了知道自己的得分外,还必须知道统计出来的( )
A、平均数 B、中位数 C、最高分 D、最低分
二、填空题(本大题12小题,每小题2分,共24分)
9、计算:(-1)÷10×![]() = 。
= 。
10、因式分解:x3-2x2+7x-14= 。
11、第五次全国人口普查公报公布,我国人口约为人,用科学计数法表示为 人(保留三个有效数字)
12、已知a+b=3,ab=2,则a2+b2= 。
13、当m=
时,x2-(3m-1)x+![]() 是完全平方式。
是完全平方式。
14、已知y是x的反比例函数,且点A(3,-4)在函数图象上,当x>0时,y是x的增大而 。
15、已知抛物线y=ax2+bx+c(a、b、c是常数,a≠0,且b2-4ac>0)的对称轴是x=1,那么ax2+bx+c=0的两根之和等于 。
16、已知等腰三角形的一个外角为108°,则其底角的度数为 。
 17、方程
17、方程![]() -2=0的解是
。
-2=0的解是
。
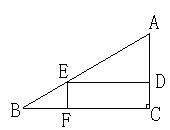
18、如图,△ABC中,∠C=90°,矩形CDEF的顶点D、E、F分别在AC、AB、BC上,BF=2,FC=4,AC=3,则矩形CDEF的面积等于 。
19、若扇形的半径是6cm,圆心角是120°,则扇形是弧长是 cm。(结果用![]() 表示)
表示)
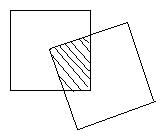 20、如图所示,边长为a的两个正方形,其中一个正方形的一个顶点恰巧在另一个正方形的中心上,则它们重叠部分(阴影部分)的面积为 。
20、如图所示,边长为a的两个正方形,其中一个正方形的一个顶点恰巧在另一个正方形的中心上,则它们重叠部分(阴影部分)的面积为 。
三、解答题(本大题共10个小题,共72分)解答本题时,要求写出主要的计算或论证步骤,否则不给分。
21、(本题6分)计算: -22÷(-![]() )-1-(-0.3)0-
)-1-(-0.3)0-![]()
22、(本题6分)已知x=![]() , 求
, 求![]() 的值。
的值。
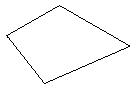 23、(本题6分)(1)请用不同的方法把下面的四边形各分成四个三角形,画出示意图,不写画法。(2)任选一个示意图,结合图形,说明四边形内角和等于360°的道理。
23、(本题6分)(1)请用不同的方法把下面的四边形各分成四个三角形,画出示意图,不写画法。(2)任选一个示意图,结合图形,说明四边形内角和等于360°的道理。


 24、(本大题6分)某商店将每台彩电按进价提高40﹪标出销售价,然后在广告中许诺将以八折优惠价出售,结果每卖掉一台彩电就赚300元。求一台彩电的进价。(提示:八折优惠价就是销售价的80﹪)
24、(本大题6分)某商店将每台彩电按进价提高40﹪标出销售价,然后在广告中许诺将以八折优惠价出售,结果每卖掉一台彩电就赚300元。求一台彩电的进价。(提示:八折优惠价就是销售价的80﹪)
 25、(本题6分)解不等式:
25、(本题6分)解不等式:![]() ≥4x,并把它的解集在数轴上表示出来。
≥4x,并把它的解集在数轴上表示出来。
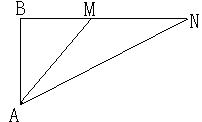
26、(本题6分)如图所示,一艘轮船在离观测站A的正北10![]() 海里处的B港出发向东航行。观测站第一次测得该船在A地北偏东30°的M处,半小时后测得该船在A地北偏东60°的N处,求这艘轮船的速度。
海里处的B港出发向东航行。观测站第一次测得该船在A地北偏东30°的M处,半小时后测得该船在A地北偏东60°的N处,求这艘轮船的速度。
27、、(本题8分)已知二次函数y=ax2+bx+c(a、b、c是常数,a≠0)的图象经过点A(-3,-2)、B(-1,-2)和C(0,1),求这个二次函数的解析式和顶点P的坐标。
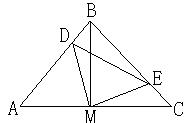 28、(本题6分)如图所示,在△ABC中,∠ABC=90°,AB=BC,BD=CE,BM⊥AC于M,求证:△DEM是等腰三角形。
28、(本题6分)如图所示,在△ABC中,∠ABC=90°,AB=BC,BD=CE,BM⊥AC于M,求证:△DEM是等腰三角形。
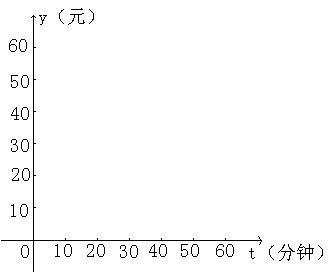 29、(本题10分)为了提高手机通信服务质量,遵义市电信局开展了多种服务业务,规定了相应的收费标准。其中使用“黔中游”卡的收费标准为:每月固定费20元,通话费每分钟0.2元;使用“神州行”卡的收费标准为:免收固定费,通话费每分钟0.6元。已知电话费=固定费+通话费。(1)分别求使用两种卡应交电话费y(元)与通话时间t(分钟)之间的函数解析式;(2)在给定的坐标系中画出它们的图象;(3)指出使用哪一种卡合算。
29、(本题10分)为了提高手机通信服务质量,遵义市电信局开展了多种服务业务,规定了相应的收费标准。其中使用“黔中游”卡的收费标准为:每月固定费20元,通话费每分钟0.2元;使用“神州行”卡的收费标准为:免收固定费,通话费每分钟0.6元。已知电话费=固定费+通话费。(1)分别求使用两种卡应交电话费y(元)与通话时间t(分钟)之间的函数解析式;(2)在给定的坐标系中画出它们的图象;(3)指出使用哪一种卡合算。
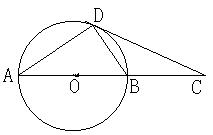
30、(本题12分)如图所示,已知⊙O的直径AB=1,延长AB到C,使BC=AB,过C作⊙O的切线CD,D为切点,连结AD、BD。
求:(1)CD的长;(2)AD︰BD的值;(3)△ABD的面积